I'm very sorry about all the inconvenience, and I would like to bear the blame. Much thanks to those who help me prepare this round. It's not their fault. And much thanks to your participation.
1581A - CQXYM Count Permutations
idea: interlude
preparation: CQXYM
tutorial: CQXYM
Assume a permutation $$$p$$$, and $$$\sum_{i=2}^{2n}[p_{i-1}<p_i]=k$$$. Assume a permutaion $$$q$$$, satisfying $$$\forall 1 \leqslant i \leqslant 2n, q_i=2n-p_i$$$. We can know that $$$\forall 2 \leqslant i \leqslant 2n,[p_{i-1}<p_i]+[q_{i-1}<q_i]=1$$$. Thus,$$$\sum_{i=2}^{2n}[q_{i-1}<q_i]=2n-1-k$$$, and either $$$p$$$ should be counted or $$$q$$$ should be counted. All in all, the half of all the permutaions would be counted in the answer. Thus, the answer is $$$\frac{1}{2}(2n)!$$$. The time complexity is $$$O(\sum n)$$$. If you precalulate the factors, then the complexity will be $$$O(t+n)$$$.
1581B - Diameter of Graph
idea: CQXYM
preparation: CQXYM
tutorial: CQXYM
If $$$m < n-1$$$, the graph can't be connected, so the answer should be No.
If $$$m > \frac{n(n-1)}{2}$$$, the graph must contaion multiedges, so the answer should be No.
If $$$m=\frac{n(n-1)}{2}$$$, the graph must be a complete graph. The diameter of the graph is $$$1$$$. If $$$k>2$$$ the answer is YES, otherwise the answer is NO.
If $$$n=1$$$, the graph has only one node, and its diameter is $$$0$$$. If $$$k>1$$$ the answer is YES, otherwise the answer is NO.
If $$$m=n-1$$$, the graph must be a tree, the diameter of the tree is at least $$$2$$$ when it comes to each node has an edge with node $$$1$$$. If $$$m>n-1 \wedge m<\frac{n(n-1)}{2}$$$, we can add edges on the current tree and the diameter wouldn't be more than $$$2$$$. Since the graph is not complete graph, the diameter is more than $$$1$$$, the diameter is just $$$2$$$. If $$$k>3$$$ the answer is YES, otherwise the answer is NO.
The time complexity is $$$O(t)$$$.
1580A - Portal
idea: CQXYM
preparation: CQXYM
tutorial: CQXYM
We can enumerate the two corner of the submatrix, calculate the answer by precalculating the prefix sums. The time complexity is $$$O(\sum n^2m^2)$$$. When we enumerated the upper edge and the lower edge of the submatrix, we can calculate the answer by prefix sum. Assume the left edge of the submatrix is $$$l$$$, and the right edge is $$$r$$$. The part of anwer contributed by upper and lower edge are two segments, we can calculate the answer by prefix sums. The middle empty part is a submaxtrix, and we can use prefix sums too. Since we have enumerated the upper edge and lower edge, the left edge part is just about $$$l$$$, and the right part is just about $$$r$$$. Then we enumerate $$$l$$$, the answer of the best $$$r$$$ can be calculated by precalculating the suffix miniums. The time complexity is $$$O(\sum{n^2m})$$$, space complexity is $$$O(nm)$$$.
1580B - Mathematics Curriculum
idea: interlude
preparation: interlude
tutorial: CQXYM
Define the dp state $$$f_{l,s,d}$$$ as the number of the permutaion length of $$$l$$$ with exactly $$$d$$$ such numbers that all the subsegments containing them have exactly $$$s$$$ different maxima in total. We enumerate the position of the bigest number in the permutaion. We call the position is $$$a$$$. The numbers before $$$a$$$ and after $$$a$$$ are independent. Then we transform the statement $$$(l,s,d)$$$ to $$$(a-1,x,d+1)$$$ and $$$(l-a,y,d+1)$$$. We also have to distribute the numbers to two parts, so the dp transformation is:
$$$f_{l,s,d}=\sum_{a=1}^{l} \binom{l-1}{a-1} \sum_{x=0}^{s}f_{a-1,x,d+1}f_{l-a,s-x-[d=k],d+1}$$$
In addition, the answer of the problem is $$$f_{n,m,k}$$$. Actually, the dp proccess is just like a cartesian tree. The time complexity is $$$O(n^2m^2k)$$$, space complexity is $$$O(nmk)$$$. However, it's enough to pass the tests.
1580C - Train Maintenance
idea: interlude
preparation: interlude
Let's distinguish the trains according to $$$x_i + y_i$$$.
If $$$x_i + y_i > \sqrt{m}$$$, the total times of maintenance and running don't exceed $$$\frac{m}{\sqrt{m}}=\sqrt{m}$$$. So we can find every date that the train of model $$$i$$$ begin or end maintenance in $$$O(\sqrt{m})$$$, and we can maintain a differential sequence. We can add 1 to the beginning date and minus 1 to the end date, and the prefix sum of this sequence is the number of trains in maintenance.
If $$$x_i + y_i \le \sqrt{m}$$$, suppose the train of model $$$i$$$ is repaired at $$$s_i$$$ day. For a date $$$t$$$ that the train of model $$$i$$$ is in maintenance if and only if $$$(t-s_i) \ mod \ (x_i+y_i) \geq x_i$$$. Thus for each $$$a \le \sqrt{m}$$$, we can use an array of length $$$a$$$ to record the date of all trains that satisfy $$$x_i + y_i = a$$$ are in maintenance modulo $$$a$$$. And for one period of maintenance, the total days aren't exceed $$$\sqrt{m}$$$. So we can maintain $$$(t - s_i) \ mod \ (x_i + y_i)$$$ in $$$O(\sqrt{m})$$$.
Thus the intended time complexity is $$$O(m\sqrt{m})$$$ and the intended memory complexity is $$$O(n + m)$$$.
Tutorial by CQXYM
Finished reading the statement, you may have thought about this easy solution as followed. Maintain an array to count the trains in maintenance in each day. For add and remove operations, traverse the array and add the contribution to the array. The algorithm works in the time complexity of $$$O(nm)$$$. Besides, we can use the difference array to modify a segment in $$$O(1)$$$. However, we can optimize this solution. For the trains of $$$x+y>\sqrt m$$$, we can modify every period by brute force because the number of periods is less than $$$\sqrt m$$$. For the trains of $$$x+y \leqslant \sqrt m$$$, the number of the periods can be large. In this case, we set the blocks, each of them sizes $$$O(\sqrt m)$$$. We can merge the modifies which are completely included in the same block, with the same length of period and the same start position in the block. It's fine to use an array to record this. Number of segments are not completely included in the block is about $$$O(\sqrt m)$$$. The total complexity is $$$O(m\sqrt m)$$$.
1580D - Subsequence
idea: interlude
preparation: interlude
First we can change the way we calculate the value of a subsequence. We can easily see the value of a subsequence $$$a_{b_1},a_{b_2},\ldots ,a_{b_m}$$$ is also $$$\sum_{i = 1}^m \sum_{j = i + 1}^m a_{b_i} + a_{b_j} - 2 \times f(b_i, b_j)$$$, which is very similar to the distance of two node on a tree. Thus we can build the cartesian tree of the sequence, and set the weight of a edge between node $$$i$$$ and $$$j$$$ as $$$|a_i - a_j|$$$. Then we can see what we are going to calculate turns into follows : choosing $$$m$$$ nodes, maximize the total distance between every two nodes. Thus we can solve this task using dynamic programming with the time complexity $$$O(n^2)$$$.
Tutorial by CQXYM
From the statement, we'd calculate the sums like $$$a_i+a_j-Min_{k=i}^j a_k$$$. When we put this on a cartesian tree, it turns out to be $$$a_i+a_j-a_{LCA(i,j)}$$$. Set the weigth of the edge $$$x \rightarrow y$$$ as $$$a_y-a_x$$$, $$$a_i+a_j-a_{LCA(i,j)}$$$ equals to the distance between node $$$i,j$$$ on the tree. Define the dp state $$$f_{i,j}$$$ as the maxium answer in the subtree rooted at node $$$i$$$, and we choose $$$j$$$ of the nodes in the subtree. Enumerate how many nodes we choose in the subtree of left-son of node $$$i$$$, number of nodes of right-son, and whether node $$$i$$$ is chose. The contribution made by the edge is its weight times the number of nodes are chose. Since a pair of node will contribute time complexity only when we are calculating the dp state of their LCA, the total time complexity is $$$O(n^2)$$$.
1580E - Railway Construction
idea: interlude
preparation: interlude
tutorial: interlude
For convenience, we first define $$$dis[u]$$$ as the length of the shortest path between node 1 and node $$$u$$$ and "distance" of node $$$u$$$ as $$$dis[u]$$$, and call node $$$u$$$ is "deeper" than node $$$v$$$ if and only if $$$dis[u] > dis[v]$$$. Similarly, we call node $$$u$$$ is "lower" than node $$$v$$$ if and only if $$$dis[u] < dis[v]$$$. We will use $$$u$$$ -> $$$v$$$ to denote a a directed edge staring at node $$$u$$$ and ending at node $$$v$$$, and use $$$u$$$ --> $$$v$$$ to denote an arbitrary path staring at node $$$u$$$ and ending at node $$$v$$$. We call two paths "intersect" if and only if they pass through at least 1 same node.
First let's focus on several facts.
- Since all edges' weights are positive, and we have to make sure that the distance of every node does not change, for any node $$$u$$$, we can only add edges starting at a node whose distance is strictly less than $$$dis[u]$$$. Besides, we can always add edge 1 -> $$$u$$$, but we can never add edge $$$u$$$ -> 1.
- Since the distance of every node does not change and the train only pass through the shortest path, if an edge is not on the shortest path at first, however we add edges it won't be on any shortest path. Thus we can first calculate the shortest path and then remove all edges which are not on the shortest path. We can easily see that the new graph is a $$$DAG$$$ (Directed Acyclic Graph). And in this graph the topological order is also the ascending order of nodes' distances. In the following part of this tutorial, we will use the new graph instead of the original graph.
- After we add all edges, every node except node 1 must have at least 2 incoming edges.
Then let's prove a lemma: if every node except node 1 exactly has 2 incoming edges, the graph will meet the requirement.
We will use mathematical induction method to prove the lemma. For an arbitrary node $$$u$$$, we suppose that all nodes whose distance is less than $$$u$$$'s has met the requirement, and we only need to prove that node $$$u$$$ also meets the requirement. Suppose the start of the 2 incoming edges is separately $$$s$$$ and $$$t$$$.
First, if $$$s$$$ or $$$t$$$ is node 1, we can simply choose $$$1$$$ --> $$$u$$$ and $$$1$$$ --> $$$t$$$ -> $$$u$$$ as the two paths and obviously they don't intersect. Thus it meet the requirement.
Second, if $$$s$$$ and $$$t$$$ are not node 1. We choose an arbitrary path $$$1$$$ --> $$$s$$$ and call it path 0. According to our assumption, we can choose two different paths starting at node 1 and ending at node $t$, and the two paths don't intersect. We call them path 1 and path 2 separately.
If path 0 and path 1 (or path 2) doesn't intersect, then we can choose path 0 and path 1 to meet the requirement. Thus we only need to consider the situation that path 0 intersect with both path 1 and path 2.
In this case, we first find the lowest and deepest node where path 0 and path 1 or path 2 intersect, and call them $$$a$$$ and $$$b$$$ separately.
If the both are the intersect points of path 0 and path 1, like the case below, we can choose path (1 -> a -> (through path 1, i.e. blue path) b -> s) and path 2.
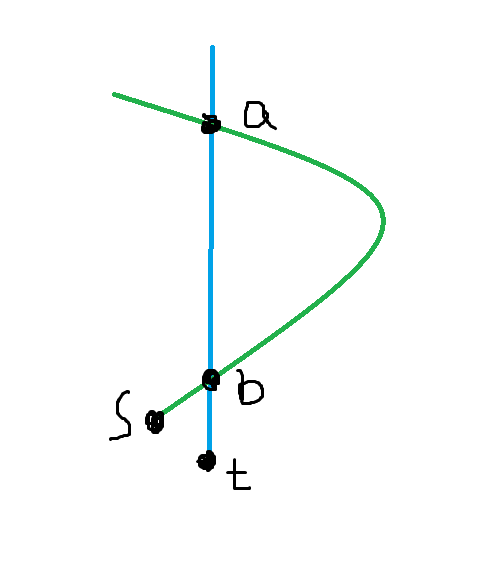
Otherwise, like the case below, we can choose path (1 -> a -> t) and path (1 -> b -> s).
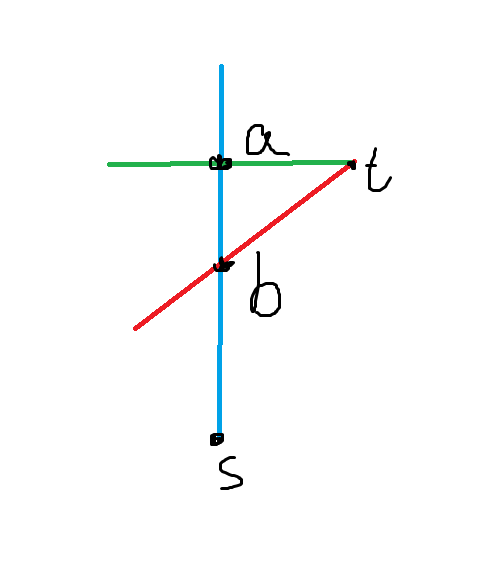
Both cases are meet the requirement.
Thus we've proved the lemma. So we only need to make sure that every node except node 1 has at least 2 incoming edges. Then we can get the following solution if $$$w$$$ is fixed:
For every node which has only 1 incoming edge, we record the start point of the incoming edge in an array. Then We scan all nodes in the ascending order of nodes' distances, and maintain the previous minima and second minima of $$$w$$$ in an array $$$val$$$, adding edges greedy. Note that we only need to maintain the index of $$$w$$$ instead of its real value. This solution consumes $$$O(n)$$$ to calculate for a fixed $$$w$$$, so the total complexity is $$$O(nq)$$$.
To accelerate the solution, let's try maintaining array $$$val$$$ while changing $$$w$$$. And we will apply all the changes in reverse order. That is, we only consider the case that $$$w$$$ is decreasing.
According to the value of $$$val$$$, we can separate the sequence into many subsegments, and we can use std::set to maintain those subsegments. For one change in $$$w_k$$$, it will affect a particular suffix of $$$val$$$, so we can first find the suffix. Then we consecutively change the array $$$val$$$ until $$$w_k$$$ is greater than current subsegment's second minima. Next we will prove that the solution works in $$$O((n+q)logn)$$$.
When we change a particular subsegment, we separate the operation into 3 types according to the relationship between $$$w_k$$$ and the subsegment's $$$val$$$.
- If $$$w_k$$$ is exactly the minima of the subsegment. This kind of operation may be done many times, but we will find that it won't change $$$val$$$ at all. So we can do them at a time using segment tree. Thus in one change we will only do it at most 1 time.
- If $$$w_k$$$ is the second minima of the subsegment. Note the fact that every subsegment must has different second minima, so this kind of operation will be also done at most once in one change.
- If $$$w_k$$$ is neither the minima nor the second minima of the subsegment. Note the fact that each time we do it, except the first time, will make the number of subsegments decrease by 1. Thus this kind of operation will be done no more than $$$n+q$$$ times.
Using std::set and segment tree, all of these operations could be done in $$$O(logn)$$$ at a time. Thus the total complexity is $$$O((n+q)logn)$$$.
In conclusion, we can solve this task in $$$O(mlogm + (n+q)logn)$$$.
1580F - Problems for Codeforces
idea: CQXYM
preparation: CQXYM
tutorial: CQXYM
If two numbers $$$a,b$$$ satisfying $$$a+b<m$$$, there can only be one number not less than $$$\lceil \frac{m}{2} \rceil$$$. Consider that cut the cycle to a sequence at the first position $$$p$$$ satisfying $$$\max(a_p,a_{p+1})<\lceil \frac{m}{2} \rceil$$$. When we minus all the numbers that are not less than $$$\lceil \frac{m}{2} \rceil$$$ by $$$\lceil \frac{m}{2} \rceil$$$, we can get a sub-problem. However, If $$$n$$$ is an even number, we may not find such a position $$$p$$$, but we can still get a sub-problem easily. For this problem on a sequence, we can divide the sequence into many segments, and each of them can not be cut by us anymore. There may be only $$$1$$$ segment, and the first, last element of the segment are not less than $$$\lceil \frac{m}{2} \rceil$$$. There may be many segments, the length of the first one and last one are even, and the rest of them are odd. To solve the problem, we define the GF A,B. A is the GF of the length of the segments are odd situation, and B is the even one. If $$$m$$$ is odd, the segment with only a number $$$[\frac{m}{2}]$$$ exists, and the GF of number of the sequence should be:
$$$B^2(\sum_{i=0} (A+x)^i)+A=\frac{B^2}{1-x-A}+A$$$
Otherwise, it is:
$$$B^2(\sum_{i=0} A^i)+A=\frac{B^2}{1-A}+A$$$.
To solve this problem, use NTT and polynomial inversion algorithm is just ok. Each time we transform a problem with limit $$$m$$$ to $$$\frac{m}{2}$$$, so the time complexity is $$$O(n \log n \log m)$$$.
UPD: Chinese editorial can be found here.










I don't get why the announcement was downvoted. I thought the problems were nice, but it was not prepared very well (typoes, convoluted statements, and many failed pretests)
I think it is mostly cordinator mistake, they could have avoided it.
i downvoted because the samples in some problems hadn't been really informative
"I don't get why the announcement was downvoted"
Immediately proceeds to explain why the announcement was downvoted in the next sentence (and as a bonus, why this editorial was not).
can we use sqrt decomposition for Div2E — Train Maintenance ?
Yes.
"we can add edges on the current tree and the diameter wouldn't be more than 3." should not it be 2 ? In second editorial.
Fixed.
The contest was very difficult . But thanks for the editorial.
I believe the contest was too tough !! and in B also 1 1 2 case was not present in pretests.
For the Div2B problem, was there any specific reason for the diameter being less than K-1? I think this added some inconvenience because K could be zero. Anyways thanks for the editorial.
I think to make case 1 0 1 a special case
It seems that it's just because the problem setters didn't want the codes to be too short.
Can someone explain the second line of problem A div2
All it says is either $$$p_{i-1} < p_{i}$$$ or $$$q_{i-1} < q_{i}$$$, but not both at once.
The only issue is typo here:
It should be:
Fixed.
It is just a formal way of saying there is a bijection between any permutation and the reversed permutation, exactly one of which will have number of consecutive increases at least n so counted. Also observe any permutation either has < n or >= n consecutive increases, so this counts all possible permutations.
forgive me but can you explain problem A solution, i am not able to understand editorial solution
Which part of my explanation do you not understand?
Actually i didnt get how the total count was (2n!)/2 :/
Let's say there is a permutation P of the given array of size 2*n . Now let's count the number of positions satisfying P[i] < P[i+1] if this count is equal to say k.
Then there will be exist some array Q ( refer to the editorial ) in which the number of positions satisfying Q[i] < Q[i+1] will be 2*n — k — 1.
So either P or Q will have atleast n positions satisfying the given condition. So for every permutation we can either take P or Q. But due to repetition we will take ( 2n! / 2 ) as the answer.
Codeforces rated div2 A ques as 800. Seriously...I have solved relatively easier 1100, 1200 range rated ques. Somebody plz tell codeforces that every div2 A ques is not 800 range one..
There were 6375 participants in Div2 and 5602 of them successfully solved problem A. Only 773 failed. So as this blog explains, rating 800 means that the participants with rating 800 had a 50% chance to solve problem A. And maybe that's how it really was. With one little caveat: those who bailed out of the contest without submitting anything, haven't been counted as participants.
Thanks for the info... I used to thought that some very high rated coders who are authorised by Codeforces rate the questions but turns out its some mathematical calculations that determines the rating based on percentage of submissions made during the contest... Its not a ryt way i think...consider a case where 10000 people read q1 of div2a out of which 5000 made submissions and about 4500 turns correct during the contest.. That ques may be is a typical 1100 rating ques but based on mathematical calculations it will be rated 800..
Div 2 A Video Editorial: Introduces the concept of a bijection which is fundamental to the solution
Div 2 B Video Editorial: Uses the basic concepts of a graph and tree to come up with a construction for the graph with minimum diameter
I can't understand the process of div2 C even after tutorial. Can anyone explain the process?
First, try to solve it as 1D array having different value, lets call this array A[]
You have a variable C carrying some information, and you are at position i in array A, Now you want to find minimum value A[j] — C for all j such that j >= i + 3.
If you perform suffix minimum on array A it's obvious the minimum will always be at A[j + 3]
Now lets back to the problem.
You will loops between all possibles rows with two variables r1, r2, and solve for the columns between r1 and r2 as 1D array problem.
At position i, the array will carry how many blocks of 1s you need to change to 0 (all blocks between the two points (r1 + 1, 1) and (r2 — 1, i — 1)), also will carry how many block of 0 you need to change to 1 (Which are at column i between two points (r1 + 1, i), (r2 — 1, i), at r1 between points (r1, 1), (r1, i — 1) and at r2 between points (r2 ,1), (r2, i -1)).
Now you perform minimum suffix on the 1D array you created and start iterating for the columns
At position i, let x be the position of column which has minimum value, so A[i+3] will have the minimum value of changes from column 1 to column x, but I need the answer from column i to column x, that's the C variable I was talking about which we need to calculate
Calculating C will be the number of 1s you need to change to 0 from points (r1+1, 1), (r2-1, i) and the number of 0s you need to change to 1 in the two rows from 1 to i
Cur = A[i+3] — C
Now $$$Cur$$$ have the minimum value for the rows and right columns, all you need now to know how many value 0s you need to change to 1s at the left column which is at position i.
Here is my submission: https://codeforces.com/contest/1581/submission/130415196
My solution to D for which I have no idea why it works:
Start with the subsequence being the entire array, then remove the element whose removal would decrease the score by the smallest amount $$$n-m$$$ times.
Edit: I just stress tested it and found that it doesn't actually work, it just got AC due to the problem not using multitest.
So basically greedy works? That's surprisingly easy for a Div1 D.
Can someone explain div2 C ,I am unable to understand it.
https://codeforces.com/blog/entry/95477?#comment-846448
How is O(n^5) passing for Div 2 D? Are the states being visited in top down dp very less or is it something else?
Please help in Div 2B (Diameter of graph).
Lets say there are 63 nodes in the graph and edges are also 63. First 62 edges are used to create a complete tree. At this moment, Max distance between 2 leaf nodes is 10 which is the diameter. I don't understand where I should place the last edge such that diameter reduces to atmax 3.
I think I am understanding the question all wrong!
You can arrange ANY graph using n nodes and m edges. The best tree (in terms of min diameter) has n-1 leaves and 1 root node. It's diameter is 2 (leaf1->leaf2 = leaf1->root->leaf2 thus distance is 2. leaf->root is one edge and distance is 1). Then it's easy to prove that if graph isn't complete, its diameter >= 2, and if it is, diameter = 1.
Its not the first time for me, but this time I'm sure its not only for me.
Reading editorial for F is really hard. I'm not even sure if its easier than reading google translate from chinese.
Can someone fix it? Or maybe, can someone in the comments give me some brief plan on how to solve it? Thanks.
Same. 130411823 is pretty readable though. (130596156 is my submission based off of it).
Brief explain of the editorial:
Consider the final sequence a[1],a[2]...a[n]. Call a[i] "x", if a[i]>= $$$\lceil m/2 \rceil$$$ ,and "y" for the other case .
It is obvious that two "x"s can't be adjacent .
For the given $$$n,m$$$. The answer can be calculated as follows:
n is even and the sequence is $$$xyxyxy..xy $$$. If you subtract each y by $$$\lceil m/2\rceil$$$ , then $$$\forall_i a_i+a_{i+1}<\lfloor m/2\rfloor$$$ . So you can add $$$2\times Ans(n,\lfloor m/2\rfloor)$$$ to the answer.
Consider the first position $$$t$$$ , that both $$$a_t,a_{t+1}$$$are "y" . You can cut between $$$t$$$ and $$$t+1$$$ ,and change the cycle into a chain like "y....y".
then you can split the chain into some segments of "yx...y...xy" . For example $$$[yxyxy][yxy][y][yxyxy][y][y]$$$.
Then consider a subproblem: $$$[x^n]F_m$$$ is the number of $$$a_1,a_2...a_n$$$ that $$$\forall_{1\leq i<n} a_i+a_{i+1}<m$$$. We will solve it later . So the contribution of this case is :
To calculate $$$F_m$$$,you can consider four cases :
Split them into some segments of ”yx...y...xy“ or ”yxyx...yx“ and turn it into the problem of $$$m/2$$$.
In conclusion , the key idea of the solution is to split the sequence into some segments where no two y are adjacent , and turn it into a problem of m/2.
What does the 'G' mean?
$$$G_i(x)=F_i(x)*x$$$
I get it. Thanks
Fm is calculated by recursion? How to calculate Fm efficiently?
Yes it is recursion ,just consider four cases:
[x...x]
[x...y]
[y...x]
[y...y]
Then $$$F_m$$$ can be represented by the sum of several $$$Godd_{m/2}^aGeven_{m/2}^b$$$,Where $$$Good_{m}(x)=G_{m}(x)\times[x\mod 2=1],Geven_{m}(x)=G_{m}(x)\times[x\mod 2=0]$$$
Hello, I want to share a few things about what I saw in today's contest.
First about quality of problems, I've only solved D1A, D1B and D1C, in theory, D1A and D1C are classical but good problems, D1B is a good problem for its position, I haven't thought D1D a lot, but it seems quite interesting.
But there were issues with preparation:
The fact about the corners not needed in D1A was annoying until the statement was changed (I noticed because in Minecraft corners can be anything), also system tests in D1A were not good enough, allowing solution who only tries small submatrices to be AC, like this one, setters would have considered creating some tests that ensure the solution is big and have some weird patterns to cut this kind os solutions.
In Div1B, why set $$$n = 100$$$ if there is not any solution to cut and expected is $$$O(n^5)$$$?, I needed a lot of constant optimizations to fit my solution into TL. It is sad that such a nice problem was turned into an optimization task, and surely a lot of participants (including me) didn't try $$$O(n^5)$$$ solution for being scared about TL. Also, why non-constant modulo?, why cut solutions with division/NTT and make simple implementations slower?.
In Div1C, maybe 1 second of time limit if the intended is $$$O(n\cdot \sqrt{n})$$$ and $$$n$$$ is up to $$$2\cdot10^5$$$ is tight, specially if you notice that naive implementation of the solution requires modulo operation a lot of times, maybe to cut $$$O(n\sqrt{n}\log{n})$$$, but still, my solution is that complexity and passed system tests, however it was hacked.
At the end, I liked and enjoyed the contest, the problems were interesting, and hopefully the authors learned about their mistakes and maybe in the future will prepare another contest with less issues that everyone can enjoy more.
It is very sad that authors put that much effort and make an interesting contest, while having so few Div1 nowadays, and people threat so bad the authors, I think the whole community needs to recognize and support more contest writers, they spend a lot of time and do their best effort to create an interesting contest and even with some issues, the problems have good quality and are enjoyable. Thanks to the authors for the contest!
Hi, I have a question about problem A. I understood instantly that the answer is (2n)!/2 but then I spent an hour trying to figure out how to calculate such big numbers in the program, and I failed. Even now I don't understand the code given in the tutorial. I tried to use the property of modulo (a*b)%m = ((a%m)*(b%m))%m but that was not helpful. Could you please explain?
You want to calculate $$$(2n)!/2$$$, that's $$$1*2*3*4*5*...*2n/2 = 3*4*5*...*2n$$$. After every multiplication your number can be big so you reduce it by immediately taking remainder. I think this submission should be easy to understand, but note
#define int long long(and don't use such defines yourself, it's bad practice):intis enough to store the remainder but not the intermediate product.Fun fact: the time limits were so tight, this contest had zero accepted div1 PyPy3 submissions (whereas the usual div 1 contests usually have at least a few dozen).
I got the right idea in Div.1 B and C but I FST because of the tight time limit and my large constant
my rank dropped from 50+ to 400+ :(
Div1 B: However, it's enough to pass the tests.
So how can I pass the tests?
Cuz you just want to get the value of $$$f_{n,m,k}$$$, and the useful states are extremely few, so we use search to take the place of the original dp process. If a state has been calculated before, just return the value instead of calculating it again.
In Problem Div1D,as I thought the time complexity when directly merging two dp states was $$$O(n^3)$$$ instead of $$$O(n^2)$$$,so I used two-pointers when merging.But I don't know whether it is correct or not.
Could someone help me prove my solution's correctness or hack it?
https://codeforces.com/contest/1580/submission/130375694
during the contest:
after the contest:
I have nothing to say...
That's why CF is down 1 min ago lol
n^5 for 100. What a nice problem.
Yes, I never think of writing that complexity code
Overall, I like the problems, but I don't like the constraints and time limits.
I'm actually surprised that the constraints and time limits weren't changed, especially after testing.
Decrease the constraints, increase the TL, and this would be a nice round.
We can solve F in $$$O(n\log n)$$$, here is a sketch:
When $$$n$$$ is even, $$$a_1 < m - a_2 > a_3 < \cdots < m - a_n > a_1$$$. So we need to count the sequences $$$0\le b_i\le m$$$ where $$$b_1<b_2>\cdots<b_n>b_1$$$. You can do inclusion-exclusion for all $$$"<"$$$. It can be solved through computing something like $$$\frac 1{1-P}$$$.
When $$$n$$$ is odd, the pattern should be a ring with $$$xy\dots yx$$$ where $$$x\le \frac m2$$$ and $$$y>\frac m2$$$. You can let $$$x \leftarrow \lceil m/2\rceil -x $$$ and then it becomes a $$$<><>\cdots$$$ again.
That's great!
However, could you please offer me the details/code and I'll update it to the editorial.
Can you update your current editorial, please? Im sorry to say that, but currently its not readable.
The editorial of problem Div1.F is really hard for me to understand, can you update it...
Thanks
orz
To make it a bit clearer for anyone else: the part about odd $$$n$$$ means that we can split our circle into segments of form $$$xy \dots yx$$$.
Can you explain it a little more clearly? I just can't understand it...
1) If n is even.
$$$a_0 + a_1 < m \Leftrightarrow a_0 \le m - 1 - a_1$$$.
So if we consider the sequence $$$ b_i = ( a_0, m - 1 - a_1, a_2, \dots, m - 1 - a_{n-1} ) $$$ then every number must belong to $$$[0; m)$$$ and we must have $$$b_0 \le b_1 \ge b_2 \le \dots \le b_{n-1} \ge b_0$$$
(if you use $$$m - a_i$$$ then some numbers are in $$$[0..m)$$$ while others are in $$$[1..m]$$$ which was a bit inconvenient to me).
Now, we apply inclusion-exclusion principle for all "$$$\ge$$$". Let's break the cycle(ignore the $$$b_{n-1} \ge b_0$$$ condition) first to make it easier.
What this means is we always keep all the $$$\le$$$ signs, and replace some of the $$$\ge$$$ signs with $$$<$$$ while ignoring the rest of $$$\ge$$$, count the numbers of sequences satisfying all the inequalities we got, multiply it by $$$(-1)^{\textrm{[# of >'s we ignored]}}$$$ and then sum it over all $$$2^n$$$(or $$$2^{n-1}$$$ since we ignore the last inequality right now) possibilities of inverting/ignoring the signs.
For example we might get something like $$$b_0 \le b_1 \wedge b_2 \le b_3 < b_4 \le b_5$$$ -- several independent chains of $$$\le$$$ and $$$<$$$ alternating. How many solutions are there to $$$b_0 \le b_1 < b_2 \le b_3 < \dots < b_{2k-2} \le b_{2k-1}$$$? It's pretty simple to find out it's $$$f_k={{m+k}\choose {2k}}$$$.
If we consider a polynomial $$$P(x)=-f_1 x - f_2 x^2 - f_3 x^3 - \dots$$$ and calculate $$$1 + P + P^2 + P^3 + \ldots = \frac{1}{1-P}$$$, then its $$$x^n$$$ coefficent gives us exactly the number we needed(multiplied by $$$(-1)^n$$$).
How to deal with the cycle? First of all, we can't use all $$$n$$$ "$$$>$$$" signs since it would mean $$$b_0>b_0$$$. Before, we always had the first "chain" that started with $$$b_0 \le b_1$$$. Now let's say the first "chain" is the one that contains the $$$b_0 \le b_1$$$ condition. It's easy to see that if this first "chain" has length $$$k$$$(e.g. $$$k$$$ "$$$\le$$$" signs), then there are $$$k$$$ positions where it could've started and other than that it's exactly the same as in the "no-cycle" case.
So you just need to consider $$$Q(x) = -f_1 x - 2 f_2 x^2 - 3 f_3 x^3 - \dots$$$ and the answer is $$$Q + Q P + Q P^2 + \dots = \frac{Q}{1-P}$$$.
2) If n is odd.
Let's say a number $$$x$$$ is big if $$$x \ge \lceil \frac{m}{2} \rceil$$$ and small otherwise. As I've said above, since two large numbers can't be next to each other, you can split your cycle into segments which look like "small-large-small-large-small". So we only need to a) find out how many possible segments there are for each possible segment length and b) how to use that information to solve the problem.
b) is very similar to the solution of part 1), except you don't need to use the PIE.
To solve a), first subtract $$$\lceil \frac{m}{2} \rceil$$$ from every large number. If $$$m$$$ is even, you just got the "no-cycle" case of part 1), however the length of your sequence is now odd instead of even.
If $$$m$$$ is odd, you have to notice that a small number $$$\lfloor \frac{m}{2} \rfloor$$$ can't be next to a large number, so you can set $$$m := m-1$$$, EXCEPT that $$$\lfloor \frac{m}{2} \rfloor$$$ still can be used in a segment of length 1.
Finally, how to deal with the fact that the sequence length is now odd? Similarly to solving the "circle" problem of part 1), we must consider the first chain separately. There are $$${m + k - 1} \choose {2k-1}$$$ solutions to $$$b_0 > b_1 \ge b_2> \dots > b_{2 k - 3} \ge b_{2 k - 2}$$$ so you just define a polynomial $$$R$$$ that has these coefficients and the answer is $$$\frac{R}{1-P}$$$(here we'll need all of its terms, not just a single one).
Thank you very much for your explanation!
It's easy to see that if this first "chain" has length k(e.g. k "≤" signs), then there are k positions where it could've started and other than that it's exactly the same as in the "no-cycle" case. What did it mean?
You need somehow to only count each arrangement only once. This isn't straightforward to do in the "cycle" case because multiplying the polynomials only accounts for the sequence of chains lengths. So in addition to that we also say that each sequence starts where the "chain" containing "$$$b_0 \le b_1$$$ starts.
And if the first "chain" has length $$$k$$$ then there're $$$k$$$ position(i.e. "$$$\le$$$" inequalities that we always keep) where it can be started, because the $$$b_0 \le b_1$$$ inequality can be at the any of $$$k$$$ positions in that chain and that position uniquely corresponds to a starting position.
Example: say $$$n=10$$$ and the chains lengths are $$$( 3, 2 )$$$. This corresponds to 3 arrangements:
$$$b_0 \le b_1 < b_2 \le b_3 < b_4 \le b_5 \wedge b_6 \le b_7 < b_8 \le b_9$$$
$$$b_8 \le b_9 < b_0 \le b_1 < b_2 \le b_3 \wedge b_4 \le b_5 < b_6 \le b_7$$$
$$$b_6 \le b_7 < b_8 \le b_9 < b_0 \le b_1 \wedge b_2 \le b_3 < b_4 \le b_5$$$
Thanks for details.
How could Div2 D dp space complexity be O(nmk) ? I thought of that dp during the contest but gave up thinking it will get a mle.
number of DP state is O(nmk)
Oops I didn't read the tutorial carefully. Sorry. That dp I thought of during the contest went slightly more complexed and have a memory complexity of O(n^2mk) or something.
I now feel so lucky to accidentally pass d1b without FST during contest!!!
By chance, I submitted my solution in C++14 and it passed systests in 1903ms. Before I submitted it, I added a small optimization which seemed quite useless: cut off states with $$$k>n-m+1$$$. It didn't make my solution run faster on samples.
After the contest, I submitted three more times:
Overall, if (I submitted in another language/I didn't add the optimization/the tests were a bit stronger) I would have FSTed! How lucky I was!
In 1C,some solutions FSTed with S=sqrt(m).
while in 1A,some solutions passed with $$$O(n^4)$$$
Why does my brute force with some prunes method with time complexity $$$O(n^2m^2)$$$ runs so much faster than standard program with time complexity $$$O(n^2m)$$$? In div2 C.
Can you please explain the implementation of div2 C / div1 A, which is given in editorial. I am not able to understand it.
It's so sad that I couldn't understand the editorial too. My solution is just brute force.
First pre-compute the prefix sums $$$dp[i][j]$$$ -- the number of obsidian blocks in the matrix with corners $$$(1,1)$$$ and $$$(i,j)$$$.
Then, consider the brute force solution that goes through all possible matrices with corners: $$$(x,y)$$$ and $$$(u,v)$$$. You can find the answer for each matrix in $$$O(1)$$$. If you write down the formula for each matrix, there will be various terms such as $$$dp[x][y]$$$, $$$dp[x][v]$$$, $$$dp[u][y]$$$ and $$$dp[u][v]$$$ and others. Now you can split them in two parts: terms that contain $$$v$$$ and terms that don't.
The terms that don't contain $$$v$$$, you will have to compute on each iteration of $$$x,u,y$$$.
But the terms that contain $$$v$$$ will not contain $$$y$$$, so you can compute them all at once for each pair of rows $$$x,u$$$ and store the pre-computed values as a min-suffix, so that for each iteration of $$$x,u,y$$$ you can find the minimum value for $$$v$$$ in $$$O(1)$$$.
I think it's possible to proof that such brute force solution with break statement actually has complexity O(n*m*(n+m)) because the worst possible value of answer during calculations is 16 (4*5-4), it means that brute-forcing of (i, j) on each row will be going only until it won't gain 16 "misblocks". If algorithm took a lot of steps in one row, it means that there's a "good floor" which will disturb all next iterations to lower rows by decreasing number of allowed misblocks.
I can't understand the solution of Problem div.2C. Can anyone explain what the solution do? plz :D
That is what's the meaning of array f?
I share the same sentiment with others. The problems are quite nice but the tight time limits really made the contest less enjoyable from the contestant perspective. I was really cautious about my $$$O(m\sqrt m)$$$ solution for C, so I had to preemptively eliminate all the mod operations 130360400 (turned out it was not needed though 130381622).
Yes, the round was less than ideal but I don't think the outburst from people is justified, either. I hope the authors can take the constructive criticism in a good manner and come back with a better round in the future.
My $$$ O(n^{2}m^{2}) $$$ solution for Portal (D1A / D2C): 130388066
Just brute force, chosing two endpoints of every rectangle. Since the answer is 16 for the rectangle of the smallest size, we break from the loop if the answer gets greater than 16. I don't think this was an intended solution or was it CQXYM?
UPD: Also not entirely brute force since I also used prefix sums for rows, columns and a 2D prefix sum.
Can you please add comments to your 2C/1A code? Not getting what the
GetSum()is doing and whatF[k]is storing.. CQXYMvideo solutions to A,B and C(div2) : solutions
https://codeforces.com/contest/1581/submission/130446025 im getting wrong answer for div2 C, can u check why pls if u have time!! Update : I got it why it gave WA
code
I guess the code above solve the problem 1A/2C in maybe O(16nm) complexity, but I can neither prove nor hack it.
The main idea is just brute force all sub-rectangle, but break immediately when there are already 16 operations(since the answer won't exceed 16) required in the M[1][x], M[x][1] and M[x][y] areas.
I passed 1581C - Portal with
4 nested loop and pragma
FYI, disabling asserts would've had bigger effect on running time than pragmas
:O
So, CartesianTreeForces!
Can somebody pls explain problem E?
Here is accepted code
Ok, i got the idea that when x + y > sqrt(m) we just go through pref sums and add or sub one to get count of trains. But i didnt get the case x + y <= sqrt(m). Here is fragments of code.
int u = x + y; for(int j = i + x;j < i + u;j++)s2[u][j % u]++;
and then to calculate the answer we need to do
for(int j = 1;j < M;j++) ans += s2[j][i % j];
Please explain how s2 massive works
In problem DIV2D/DIV1B Mathematics Curriculum, I find it hard to understand the dp transition function. In the tutorial, it is stated that:
However in the code, the result is returned as $$$f_{n,0,k}$$$. Also I cannot understand why $$$d$$$ will become $$$d+1$$$ during recursion. Why will the count increase when we have a smaller subsequence?
I agree it does not follow from the definition given. I think they've just replaced their original definition $$$d$$$ with $$$k+1-d$$$ or something. You can see this because they have $$$s-x-[d=k]$$$ which should (under their written definition) be $$$s-x-[d=1]$$$. (This is Iverson bracket notation). Maybe CQXYM help explain or update the tutorial?
It's also possible that I misinterpret how they define $$$f_{l,s,d},$$$ but I think it's just a mixup.
For those of you who don't understand the div1 A / div2 C tutorial, I will try give my best explanation. Prerequisite: prefix/suffix sums.
The idea is that we first suppose that we know what the top and bottom rows of the portal are (we don't actually so we will iterate over all of them in our first two loops), then now all we have to do is find out where the left and right parts of the portal lie. So let's try fixing a left side (we will try every left side we can). Now all that we need to do is find out what's the best right side for which we can build a portal.
Our right side must satisfy the two properties of the problem: - it is at least 3 away from the left side - it has the minimum changes out of all the right sides
So let's draw out a diagram of what all the possible choices look like.
first image: https://i.imgur.com/uMm0Gve.png (didn't want to embed for space reasons) second image: https://i.imgur.com/AzMqaIJ.png
The changes you need to make are circled. Notice out of all the options in the second image, you will want to take the minimum one.
Notice that as you move rightways, you have some changes that stay forever, for example all the changes in the center of the portal with right side
rneed to be emptied, but they will also need to be emptied for all right sides greater thanr, this is the most important point! This also means that when you movelforward by one tol + 1, all the possibilities forrwill only have their number of changes (which are written in blue in the second image) increased by the same constant amount, meaning the minimum will be in the same position! All that changes is the number of changes needed for the left side, and you have to make sure the right side minimum is beyondl + 2(because the portal must be 4 wide). So — ifldenotes the index of the left side — what we want is to be able to query is "what is the smallest number of changes if i pick a right side froml + 3and beyond, which we can do with a suffix minimum.Steps: 1. Iterate over all valid top and bottom row pairs,
topandbot. 2. Calculate the number of changes needed if the left side is at0(you don't need to factor in the cost of changing the left side) and the right side is atrfor all r and store it in an arraynum_changes[m]. 3. Create an arraysuffix_min_index[m]in whichsuffix_min_index[i]stores the index of right side with the minimum number of changes beyondi. 4. Iterative over every left sideland then getr = suffix_min_index[l+3]and calculate the cost of the portal surrounded bytop,bot,l, andr. 5. Minimise over all possible combinations.Complexity O(n^2m)
Gonna take my own shot at div1F since the editorial quickly switches to alien language.
If we pick values $$$\gt (M-1)/2$$$ and $$$\le (M-1)/2$$$, we can "cut" the circle between each pair of adjacent $$$\le (M-1)/2$$$, giving one or more "sequences" to solve independently, where small and large values alternate in each sequence. There are 2 cases here for linear and cyclic sequences.
First, a reformulation of the problem for one sequence. We have an integer $$$S$$$ (roughly $$$M/2$$$), a length $$$k$$$ and want to count sequences $$$a_0,a_1,\ldots,a_{2k}$$$ such that $$$1 \le a_i \le S$$$ and $$$a_{2i} \le a_{2i-1},a_{2i+1}$$$; in the cyclic case, we just add the condition $$$a_0=a_{2k}$$$. To see the equivalence to "sums of adjacent elements $$$\le M-1$$$", just subtract $$$1$$$ from everything and replace $$$a_{2i+1}$$$ by $$$M-a_{2i+1}$$$, then the odd-indexed elements are large and even-indexed ones are small.
Let's try simple slow DP. The number of sequences is $$$dp(0,a_0,a_0) = 1$$$ and $$$dp(k,a_0,a_{2k}) = \sum_{b=1}^S (S+1-\max(b,a_{2k})) \cdot dp(k-1,a_0,b)$$$. This is matrix multiplication; the matrix with elements $$$S+1-\max(i,j)$$$ is just the square of "$$$1$$$ if $$$i+j \le S$$$ else $$$0$$$", i.e. the matrix corresponding to "take suffix sums, reverse" when applied on a vector. Let's denote this matrix by $$$M$$$, then $$$dp(k) = M^{2k}$$$. For cyclic sequences, we want its trace, for linear ones we want its sum, which is the top left element of $$$M^{2k+2}$$$.
Let $$$P = \prod (x-r_i)$$$ be the characteristic polynomial of $$$M$$$. Since trace of n-th power = sum of n-th powers of eigenvalues, we want the sum of $$$2k$$$-th powers of roots of $$$P$$$;
gives us a way to find that.
OTOH the top left element is in OEIS as "number of distributive lattices" and the generating function over powers of $$$M$$$ is $$$A/P$$$, where $$$A$$$ is a polynomial very similar to $$$P$$$ (characteristic for $$$S-1$$$ only with different signs of coefficients). From OEIS, we also find that the coefficients of $$$P$$$ are binomial coefficients.
How do we use that to find the answer? If $$$N$$$ is even, there are 2 ways to place each cyclic sequence in the circle, otherwise there are 0 ways. Any number of linear sequences can be put next to each other; if $$$B$$$ is the generating function for the number of ways to create one linear sequence with length $$$2k+1$$$ (even-indexed coefficients are $$$0$$$), then the generating function for exactly $$$n$$$ such sequences is $$$B^n$$$ and for any number is $$$\sum B^n = 1/(1-B)$$$. If we fix the length $$$2k+1$$$ of the sequence covering the first element on our circle, we still have $$$2k+1$$$ ways to place this sequence on the circle and the remaining $$$N-2k-1$$$ elements are covered by any number of sequences.
The time complexity is the same as for $$$O(1)$$$ polynomial multiplications and inversions. I simply used $$$1/(1-p) = \sum p^k = \prod (1+p^{2^k})$$$ for $$$O(N \log^2 N)$$$.
div1E: I think I solved it in a O(quadratic) way (see my first AC submission, 4 identical inner while-loops), it'd be worth a countertest.
in 1581B, if m = 2*(n-1), then won't the diameter be 1? We can achieve that by joining each node with node 1 and then joining the rest n-1 nodes with each other like a polygon. CQXYM if possible can you please reply
That's not right
If there's no edge between node x,y
Distance between x,y > 1
Diameter > 1
Can someone help me understand the editorial for Div1A, I don't understand how they reduced the time complexity from O(n^2*m^2) to O(n^2*m). I understood the solution for former time complexity. Thanks a lot.
Although it really can, I still want to ask why 5*10^9 per second is enough to pass in 1B
I know i am necroposting but for the Div2B the examples aren't really well explained
how is the answer for 4 6 3 only 1? I am trying to construct a graph with minimum diameter and it is at leeast 2
Hey, you can create a graph node with 6 edges with a maximum diameter of 1 i.e. all the nodes will be connected to every other node. I know they have mentioned that the graph will not contain loops and it is an undirected graph. But that is the only graph that we could create. I think the author might have phrased the question incorrectly, hence there might be a confusion.
Can someone figure out the mistake in my submission 228786131 for problem 1580A - Portal.
Take a look at Ticket 17109 from CF Stress for a counter example.
Could anyone tell me why am i getting the wrong answer for test 2
https://codeforces.com/problemset/submission/1581/230048983