Don't see any post devoted to it yet, so start here.
Apart from the first two pretty standard problems, problem 3 was really interesting (at least, for lovers of math.stat/econometrics like me). Those who got it correct — how did you solve it?
I tried different statistics for permutations separation, the best one I found is p[i]^3 * i, it gives about 85% of cases correct, but unfortunately this is not enough to pass (we need ~90%).









 , and, given A, B cannot exceed
, and, given A, B cannot exceed 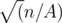 . Then all solution is just two cycles:
. Then all solution is just two cycles: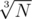 . That's why all similar solutions and maybe some other streetmagic that has anything common with divisors of N, should get AC.
. That's why all similar solutions and maybe some other streetmagic that has anything common with divisors of N, should get AC.
