
This wouldn't have been possible without all of the recent hacks that propels me this far. It was truly a miracle. I owe all of you (especially those involved in hacking solutions) a big thank you.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 2 | maomao90 | 160 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 9 | TheScrasse | 144 |

This wouldn't have been possible without all of the recent hacks that propels me this far. It was truly a miracle. I owe all of you (especially those involved in hacking solutions) a big thank you.
In last night AtCoder Beginner Contest, my submission for problem D received a Compile Error verdict using GCC (link). That very same code (besides including some library manually because Clang doesn't have bits/stdc++.h) got accepted when I used Clang (link).
More on the error, I tried to read the error message and it seemed to be an error about std::set. However the message was too long for me to either understand it or google it (man I hate C++ error messages).
./Main.cpp: In function ‘int main()’:
./Main.cpp:56:34: warning: comparison of integer expressions of different signedness: ‘std::stack<int>::size_type’ {aka ‘long unsigned int’} and ‘int’ [-Wsign-compare]
56 | if(pile[a.id].size() == k){
| ~~~~~~~~~~~~~~~~~~^~~~
./Main.cpp:74:34: warning: comparison of integer expressions of different signedness: ‘std::stack<int>::size_type’ {aka ‘long unsigned int’} and ‘int’ [-Wsign-compare]
74 | if(pile[a.id].size() == k){
| ~~~~~~~~~~~~~~~~~~^~~~
In file included from /usr/include/c++/9/map:60,
from /usr/include/x86_64-linux-gnu/c++/9/bits/stdc++.h:81,
from ./Main.cpp:1:
/usr/include/c++/9/bits/stl_tree.h: In instantiation of ‘static const _Key& std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_S_key(std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_Const_Link_type) [with _Key = node; _Val = node; _KeyOfValue = std::_Identity<node>; _Compare = comp; _Alloc = std::allocator<node>; std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_Const_Link_type = const std::_Rb_tree_node<node>*]’:
/usr/include/c++/9/bits/stl_tree.h:1929:36: required from ‘std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::iterator std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_M_lower_bound(std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_Link_type, std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_Base_ptr, const _Key&) [with _Key = node; _Val = node; _KeyOfValue = std::_Identity<node>; _Compare = comp; _Alloc = std::allocator<node>; std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::iterator = std::_Rb_tree_iterator<node>; std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_Link_type = std::_Rb_tree_node<node>*; std::_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::_Base_ptr = std::_Rb_tree_node_base*]’
/usr/include/c++/9/bits/stl_tree.h:1282:56: required from ‘std::_Rb_tree<_Key...
Can anyone give me some insights on this problem?
I like sorting algorithms very much, and I usually come up with weird ideas for sorting. Sometimes I wonder would those work properly, and now when I finally have the time from social distancing, I decided to start a series on my eccentric ideas — Weird sorts.
As an introductory problem for Dynamic Programming, you all probably know about the Longest Increasing Subsequence problem (LIS). But what if we apply this… to sorting? Today in the first blog of the Weird sorts series, I introduce to you… the LIS sort.
The core idea is to extract the LIS from the current array and repeat it until the current array is empty. It can be shown that this process always terminates, because there will always be a LIS that have a size of at least 1, thus at each pass, we will always take at least 1 element away from the array. In the implementation, we will first find the LIS of the array and separate the LIS from the rest of the array. We will then recursively perform the LIS sort on the remaining items, and merge them with the LIS using the same technique in Merge sort. The pseudocode looks something like this:
lis_sort(array A){
find_lis(A);
array LEFT, RIGHT;
for(i : elements of A)
if(i is in LIS) insert i to LEFT;
else insert i to RIGHT;
lis_sort(RIGHT);
merge(LEFT, RIGHT);
}
For better understanding, see this animation. The flaw of this algorithm lies in the number of passes that it must perform. In the worst case, the array will be in a non-decreasing order, requiring N passes to completely empty the array. Assuming you are using the standard way of finding LIS, each pass will cost $$$O(N^2)$$$, making the total complexity of this algorithm $$$O(N^3)$$$. Below are the tables of runtime with different types of arrays.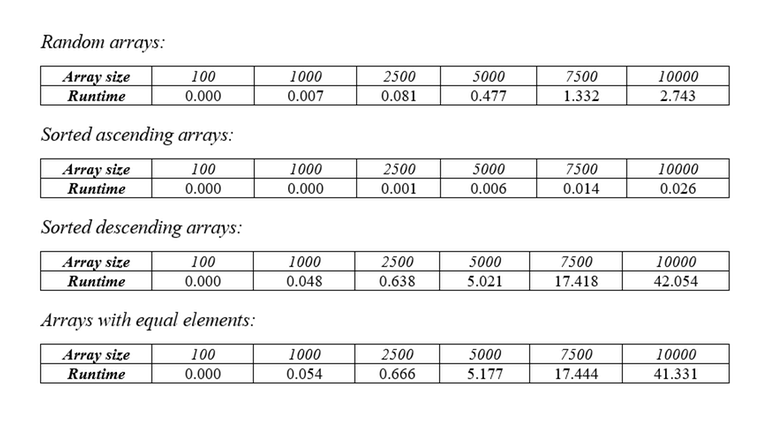
The most time-consuming part of the sort is the step where we are looking for the LIS, which costs $$$O(N^2)$$$, so we should start optimizing from there. For optimizing the LIS problem from $$$O(N^2)$$$ to $$$O(N * \log{N})$$$, there have been many pages and articles written about this, so you should look them up for yourself. Here’s my favorite site: link.
Other than that, the rest of the code is the same. By reducing the cost of finding LIS from $$$O(N^2)$$$ down to $$$O(N * \log{N})$$$, we have reduced the worst-case complexity of the sort from $$$O(N^3)$$$ to $$$O(N^2 * \log{N})$$$. Again, here are the tables of runtime with different types of arrays.
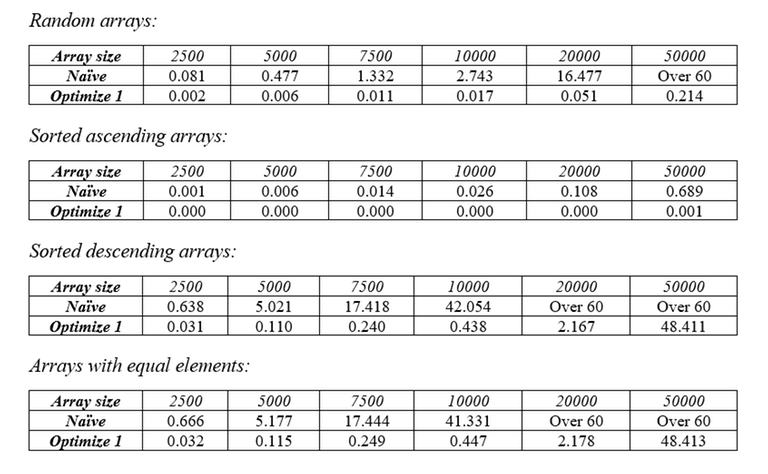
In the last 2 tests we can see that the sort performs exceptionally bad when it comes to descending arrays and arrays with equal elements. Also, when a LIS is taken from an array, there are high chances that the remaining items will form a non-increasing subsequence (this isn’t always the case, however). So, by reversing the remaining array, we increase the chance of more items being taken away from it in the next pass, thus improving the runtime of the average case and the case where the array is decreasing. Here are the tables of runtime with different types of arrays.
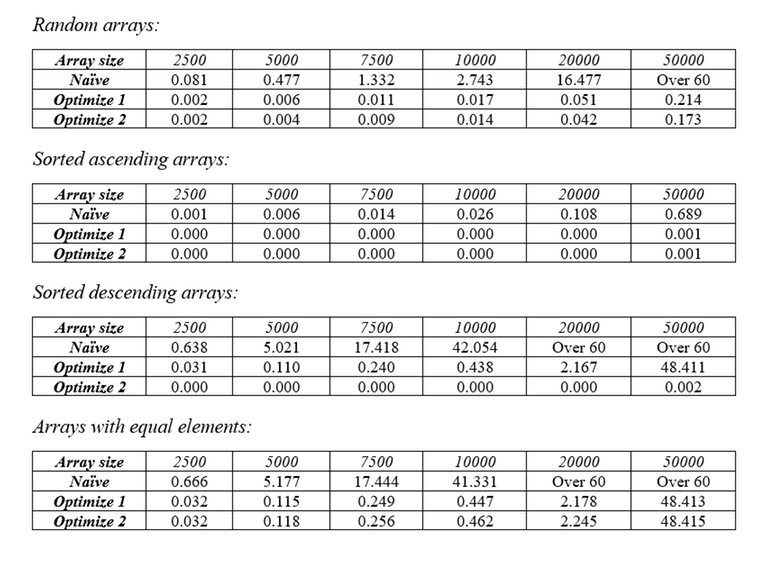
You may realize that it still performs pretty bad in the case where the array contains equal elements. It’s easy to fix this, however: instead of finding the longest increasing subsequence, we will find the longest non-decreasing subsequence. This makes sure that all equal elements are covered in one pass. Surprisingly, this even lowers the upper bound of the number of passes the sort needs to do.
How? Well first, let’s call the number of increasing subsequences is $$$A$$$ and length of the shortest one is $$$B$$$. Because the array is reversed on each pass, so either the longest increasing subsequence or an element of every other increasing subsequence is taken. Therefore, the last subsequence we take will be the shortest one (providing we didn’t take all of its elements before), so the number of passes should be $$$\min(A,B)$$$.
Now we will try to generate an array that maximizes $$$\min(A,B)$$$, which is basically the worst case. First, let’s fix the value of $$$A$$$ and maximize $$$B$$$ based on $$$A$$$. We have:
In the above equation, $$$L_i$$$ denotes for the length of the $$$i_{th}$$$ increasing subsequence. For some $$$k$$$, let $$$L_k$$$ be the length of the shortest increasing subsequence. We will have:
ㅤ
So, when B is maximized, $$$N=A*B$$$. From the equation we just deducted, we can show that the upper bound of $$$\min(A,B)$$$ is $$$\sqrt{N}$$$. To prove it, let’s assume that $$$\min(A,B)>\sqrt{N}$$$.
ㅤ
Hence, in the worst case, $$$min(A,B) = \sqrt{N}$$$. Since we need 1 pass to take the longest subsequence and 1 extra pass to take the first element of every other subsequence, the number of passes will never exceed $$$2\sqrt{N}$$$. So, the time complexity of this sorting algorithm is $$$O(N\sqrt{N} * \log{N})$$$. Of course, that’s just all the theory, let’s see how this optimization actually performs in benchmarks. Here are the tables of runtime with different types of arrays.
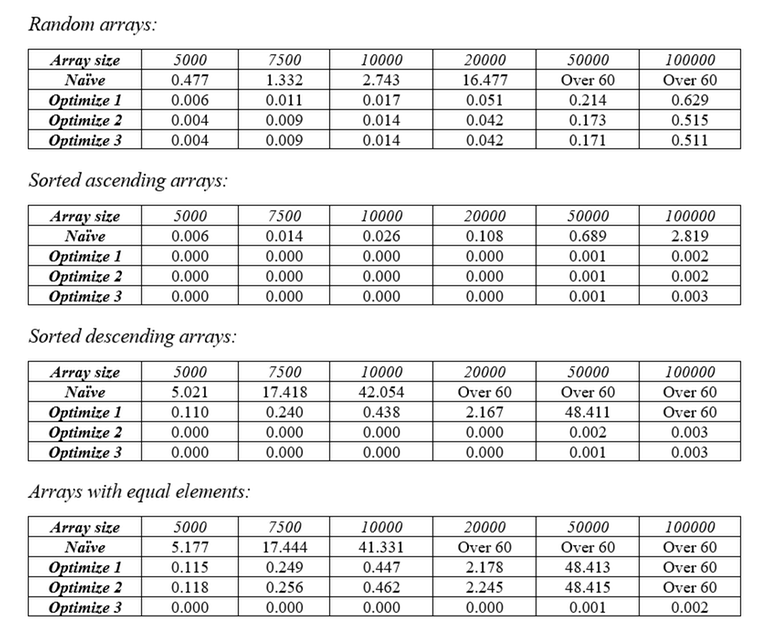
Since it performs pretty good even in edge cases, let’s put it against the real pros on the battle. Here’s the table of runtime with the LIS sort and various other sorts on random arrays.

While it was much faster than its unoptimized variants, it’s having a hard time trying to keep up with other sorts. This is due to the extra $$$O(\sqrt{N})$$$ cost of processing different passes, compared to other sorts that perform only in $$$O(N * \log{N})$$$.
All tests in this blog are benchmarked with an i7-1165G7 running at 3.30 GHz with 16 GB of RAM. All numbers were randomly and uniformly generated in the range $$$[1, 10^6]$$$ using the testlib.h library (source). Execution time was measured in seconds. The codes were executed on CodeBlocks 20.03 using C++14 and Release build target. Tests were repeated 20 times and the final value was taken from the average of 20 values.
Here are all the source codes I used to benchmark: link
To be honest, I don’t think there are any practical uses of this sort. There are many other sorting algorithms that are both faster, and more memory efficient. However, I did learn a lot while doing research and looking for proofs, especially about inequalities.
Special thanks to CatnipIsAddictive and horigin who helped me with the proofs, and to my friends who proofread this blog. Also this is the first time I write such a long blog, so mistakes are inevitable. Please comment about logical errors or grammar mistakes if you find any, or just share your thought. Thank you all for reading my little blog.
I've just came up with an optimization for problem M of AtCoder Educational DP contest (link) which only uses mathematical deductions and needs no use of data structures. If you want a brief solution that uses prefix sum, there's already a pretty great blog here.
First, let $$$dp[i][k]$$$ be the number of ways of distributing candies to the first $$$i$$$ kids and have $$$k$$$ candies left. We can try giving the $$$i_{th}$$$ kid $$$0$$$, $$$1$$$, $$$2$$$, ... candies and the number of candies left should be $$$k$$$, $$$k - 1$$$, $$$k - 2$$$, ...
This leads to the recurring formula:
This formula has $$$N * K$$$ states, and since $$$a_i$$$ can be as large as $$$K$$$, each transition costs $$$O(K)$$$ which makes the total complexity $$$O(N * K^2)$$$. Clearly with $$$K \leq 10^5$$$, this won't get us anywhere, so let's optimize it.
For a moment let's forget $$$dp[i][k]$$$ and examine $$$dp[i][k - 1]$$$ instead. Based on the recurring formula we have:
ㅤ
Let's do some magic to this formula. By expanding this a bit, we have:
ㅤ
Notice how I merged the term $$$\color{cornflowerblue}{dp[i - 1][k - 0]}$$$ into the summation. Now, some of you will realize that $$$\sum_{j = 0}^{a_i} dp[i - 1][k - j]$$$ is also conveniently $$$dp[i][k]$$$, so we can rewrite the formula as:
ㅤ
And behold, the formula which only costs $$$O(1)$$$ for transition! Just by using some rearrangements, we have a totally new recurring formula that allows us to solve the problem in $$$O(N * K)$$$, and this is just beautiful.
Thanks for reading my blog. Upvote if you like it, downvote if you don't and have a good day!
Have you ever wanted to look for that wrong testcase in your past submission to debug your code, but instead saw this?

Or this?

And countless more...



You got the point. It felt so annoying when you just needed that one small testcase for debugging, but the box was way too small to show all of them and your precious testcase was unluckily the one that was buried deep down. It would be nice if there was an option to show the full test (in a new separate tab maybe) or just let the participants download the testdata once a contest ends. I've had to cope with this situation for 2 years, and I just hope that somebody will take a look at this.
Thanks for reading my blog.
I'm solving my school's DP problem set. Since it's not in English so I'll try my best to translate the problem.
There is a wall of N blocks ($$$N \leq 5000$$$), the block at the $$$i_{th}$$$ position has the color of $$$c_i$$$ ($$$1 \leq c_i \leq 5000$$$ for all $$$i$$$).
A painter needs to paint the so all blocks of the wall have the same color. It can be whichever color, it just needs to be the same for all blocks. One at a time, he does the following operation: Choose a segment of the wall, then use a color to paint all the blocks in that segment to the same color.
As a professional painter he knows that if he paints the same color to 2 blocks with different colors, the color will end up distorted, so he only paints a segment of which all the blocks have the same color. Because he is lazy, tell him the minimum operations he needs to paint the wall.
Sample input:
4
5 2 2 1Sample output: 2
Explanation:
First he can paint the segment [2, 3] to color 5. The wall becomes 5 5 5 1.
Then he can paint the segment [1, 3] to color 1. The wall becomes 1 1 1 1.
I've came up with a DP solution that looks like this: Let $$$dp[l][r][k]$$$ be the minimum operations needed to paint the segment $$$[l, r]$$$ to the same color, with $$$k$$$ is a boolean to identify whether the segment should be painted to the left part's color or the right one.
My transition formula is:
where $$$color[l][r][k]$$$ is the color of the segment $$$[l, r]$$$ after being painted optimally. This formula has $$$N^2$$$ states and each transition costs $$$O(N)$$$, which makes the time complexity of this approach $$$O(N^3)$$$ — too slow for the problem's constraints.
Is there anything I can do to speed up the transition part? Or do I have to tackle this problem from a different approach?
So I had a regional contest yesterday, and it had a problem like this:
You are given N binary strings with the length of M ($$$N * M \leq 10^5$$$) and Q ($$$Q \leq 2*10^5$$$) queries. There are 2 types of query:
1 i j — Flip the $$$j_{th}$$$ bit at the $$$i_{th}$$$ string.
2 x y — Count the number of positions $$$i$$$ where the $$$i_{th}$$$ bit in the $$$x_{th}$$$ string and the $$$y_{th}$$$ string differ.Sample input:
3 3
110
011
000
3
2 1 2
1 3 1
2 1 3Sample output:
2
1
I wasn't able to come up with a proper solution so I decided to bruteforce instead. To make my code a little bit faster I converted all the strings to a long long vector, so I could handle query 1 with bit operations. For query 2, I noticed that if I use the XOR operation on 2 masks, the answer should have the bits on at positions which the 2 masks differ. Therefore I just had to use __builtin_popcount to count the 1 bits in the answer. Since each long long type has 64 bits, that reduced my vector size 64 times the size of the original string, thus the number of operations reduced by 64.
Theoretically my code was still $$$O(Q*M)$$$, just 64 times faster. I calculated the worst case, which was $$$3*10^8$$$, and I guaranteed that I would have some nasty timeout tests. But magically somehow, my code was accepted. I didn't believe it at first, thinking it was judged on pretests, but then I asked the organizers and they confirmed that the codes were judged on main tests.
How could this possible? Was my code actually accepted or it was just weak tests? And how can I solve this problem, the proper way?
I recently wrote a comment here. While the others rendered correctly, this one didn't:
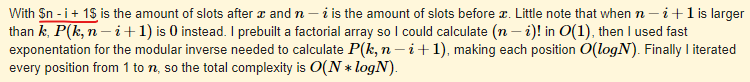
At first I thought it was my browser, so I fired up another one and it was still the same. I don't think I wrote it wrong because I used the same phrase $$$n - i + 1$$$ in the next sentence and it managed to render correctly (and also here). Did I do something wrong or is it a bug?
| Name |
|---|


