Hello,
Since the editorial posted for the ACPC 2018 is rather complicated (no offense), I decided to write my own tutorial with much simpler solutions. There are two problems missing, and, hopefully, they will be available soon. Hope you like it!
A tree has all its edges as bridges (initially  bridges).
bridges).
Joining the end-points of a simple path with length 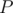 edges, removes
edges, removes 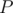 bridges from the tree (resulting in
bridges from the tree (resulting in 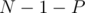 bridges).
bridges).
Initially, all edges of the given tree are bridges since removing any of them disconnects the graph. So, we start with  bridges. Joining the end-points of a simple path with length
bridges. Joining the end-points of a simple path with length 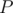 edges, removes
edges, removes 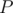 bridges from the tree (resulting in
bridges from the tree (resulting in 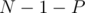 bridges). Since we want the resulting graph to have the number of bridges in
bridges). Since we want the resulting graph to have the number of bridges in  , then
, then 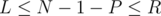 which means
which means 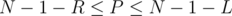 . So, all the problem is asking for is the number of simple paths
. So, all the problem is asking for is the number of simple paths 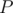 of length in the range
of length in the range 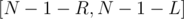 since these are the paths that give the desired number of bridges when short-circuited.
since these are the paths that give the desired number of bridges when short-circuited.
How will we count the number of paths with the given length? Centroid Decomposition! Consider the centroid tree where every vertex is the centroid of its subtree. Every path between two vertices in the initial tree passes through their lowest common ancestor (LCA) in the centroid tree. We will pick a vertex as the LCA and check for all paths that pass through it.
Consider the vertex  to be the centroid of the initial tree. For every node
to be the centroid of the initial tree. For every node  in the tree, if
in the tree, if  has a distance
has a distance  from
from  ,
,  should be matched to a vertex
should be matched to a vertex 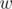 with distance to
with distance to  in the range
in the range 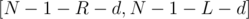 such that
such that  in the centroid tree. To be sure that
in the centroid tree. To be sure that  and
and 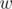 have
have 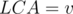 , they should be reachable from different neighbors of
, they should be reachable from different neighbors of  in
in 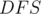 . So, perform a
. So, perform a 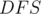 on each child of
on each child of  in order and record the distances of the encountered nodes from
in order and record the distances of the encountered nodes from  . When finished with a certain child, record these distances globally. In the next child
. When finished with a certain child, record these distances globally. In the next child 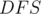 , whenever a node is encountered, check how many vertices in the previous child match with it and add the value to the answer. When done with this child, also record its values globally so that future vertices can match with the current ones. Keep in mind that vertices with a distance from the centroid in the range
, whenever a node is encountered, check how many vertices in the previous child match with it and add the value to the answer. When done with this child, also record its values globally so that future vertices can match with the current ones. Keep in mind that vertices with a distance from the centroid in the range 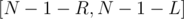 also form paths between them and the centroid, so they are counted without a match (since the centroid is matched to them).
also form paths between them and the centroid, so they are counted without a match (since the centroid is matched to them).
When done with this process, we would have found all the paths passing through  . Now, delete
. Now, delete  from the tree and repeat the same process on each of the formed components (which are also trees). For each component, find its centroid and count the number of paths through it.
from the tree and repeat the same process on each of the formed components (which are also trees). For each component, find its centroid and count the number of paths through it.
Now, what is an efficient way of counting the number of nodes with a certain distance from the chosen root? Using a BIT or Fenwick tree. When done with a child of the current centroid, update the 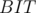 with the gathered values of distances. For a certain distance, increment its corresponding position in the
with the gathered values of distances. For a certain distance, increment its corresponding position in the 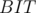 with the number of vertices with this distance from the centroid. Whenever we want to change the centroid and repeat, we empty the
with the number of vertices with this distance from the centroid. Whenever we want to change the centroid and repeat, we empty the 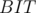 and fill it with zeroes.
and fill it with zeroes.
All 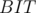 operations are done in
operations are done in 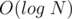 and performing
and performing 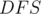 continuously on the centroids of components is
continuously on the centroids of components is 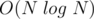 since no component is of size greater than
since no component is of size greater than 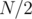 . (See definition of centroid)
. (See definition of centroid)
Complexity 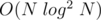
What is the probability of hitting a certain polygon?
The polygons are similar. By what factor does the inner polygon decrease?
Consider this figure:
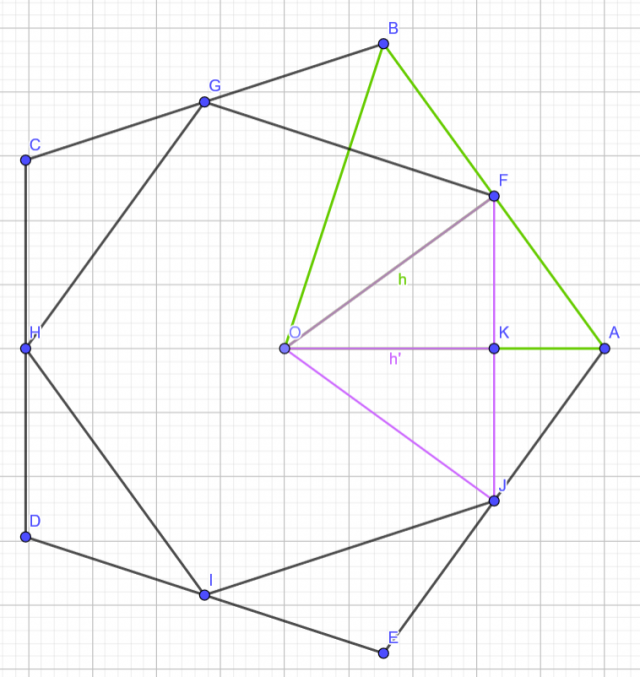
Our aim is to find the ratio by which the inner polygon decreases since the two polygons are similar. It is easy to prove that  and
and 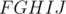 are similar, so there exists a ratio of similarity
are similar, so there exists a ratio of similarity 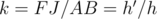 .
.
Since the polygons are all regular, then triangles 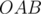 and
and 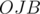 are isosceles with vertex
are isosceles with vertex  and heights (medians, perpendicular bisectors, angular bisectors)
and heights (medians, perpendicular bisectors, angular bisectors) 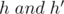 respectively.
respectively.
Triangle  is right at
is right at 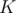 . Let
. Let  .
. 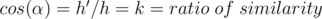 .
.
However, since the polygons are regular, then 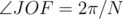 . And, since
. And, since 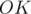 is also an angular bisector of the angle, then
is also an angular bisector of the angle, then 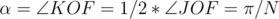 . So,
. So, 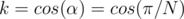 .
.
The ratio of areas then becomes: 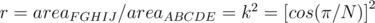
The probability of hitting the first type of nuts, in the first (outermost) polygon, is  since the first polygon is always hit. The probability of hitting the second nut type is
since the first polygon is always hit. The probability of hitting the second nut type is  since the second polygon is
since the second polygon is  times smaller than the first. For the following nut types, the probabilities are
times smaller than the first. For the following nut types, the probabilities are 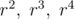 , and so on...
, and so on...
So, the expected value of nut types hit then becomes:  . Since
. Since  , then
, then 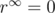 .
.
Hence, 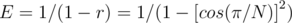 , which is the expected number of nut types hit by one fork. Since
, which is the expected number of nut types hit by one fork. Since  people will dip their forks, then the answer to print is
people will dip their forks, then the answer to print is 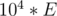 .
.
Complexity 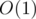
Map the coffee costs based on name and type.
This problem is pure implementation. First, you have to map the coffee prices based on name and type. One way to do this is to create a map between name and a 3-tuple. Another way is to map the coffee type and name together, 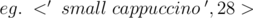 . For every person, find the price of his/her coffee from the mapping, and let this value be
. For every person, find the price of his/her coffee from the mapping, and let this value be 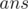 . Since there is also the delivery cost of 100 divided by all the people,
. Since there is also the delivery cost of 100 divided by all the people, 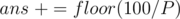 . Also, if the number is at a distance one from a multiple of 5, we have to change it to this multiple.
. Also, if the number is at a distance one from a multiple of 5, we have to change it to this multiple.
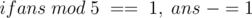
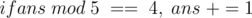
And then print the person's name followed by the answer. Repeat for all the people.
Complexity 
 and
and 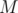 are large, but what about
are large, but what about 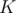 ? Do we care about non-white chocolate cells?
? Do we care about non-white chocolate cells?
Clearly, we cannot do the counting on  since that is too large. However,
since that is too large. However, 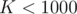 , so we can do our looping only on the white chocolates. In all cases, the count of white chocolates will remain the same and will only change when we encounter a white chocolate.
, so we can do our looping only on the white chocolates. In all cases, the count of white chocolates will remain the same and will only change when we encounter a white chocolate.
Initially, there are no perfect sub-grids until the first white chocolate is reached. We walk on the 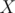 coordinates, and for every
coordinates, and for every 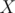 , loop on all
, loop on all 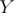 values and check. This will guarantee at most
values and check. This will guarantee at most  operations.
operations.
First, put all given 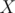 values into a set (or map) such that they are sorted in increasing order and without duplicates. For every
values into a set (or map) such that they are sorted in increasing order and without duplicates. For every 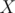 value in this list,
value in this list, 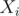 , let
, let 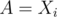 and
and 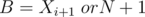 (if last element).
(if last element).
Now, loop on all white chocolates 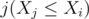 and store the count for every
and store the count for every 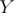 value in a map (
value in a map ( = number of white chocolates with
= number of white chocolates with 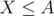 and
and  ). Now, keep a
). Now, keep a 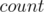 value (number of white chocolates until now) and an
value (number of white chocolates until now) and an 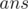 value (the number of perfect sub-grids until now), initially
value (the number of perfect sub-grids until now), initially  , and loop on the
, and loop on the 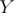 values in the map in increasing order. For a certain
values in the map in increasing order. For a certain 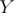 value,
value, 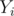 , add
, add 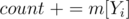 . If
. If 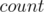 is odd,
is odd, 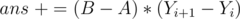 (replace
(replace  by
by 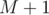 if last element). This correct since all the sub-grids from this odd count are perfect until the next white chocolate horizontally or vertically. And, before any white chocolate is encountered, there are no perfect sub-grids to count.
if last element). This correct since all the sub-grids from this odd count are perfect until the next white chocolate horizontally or vertically. And, before any white chocolate is encountered, there are no perfect sub-grids to count.
The answer to print is 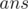 (the number of perfect sub-grids) and
(the number of perfect sub-grids) and 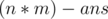 since there are exactly
since there are exactly 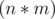 sub-grids starting at
sub-grids starting at 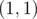 .
.
Complexity 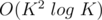
The chosen substring should always be a prefix of some string.
How does putting all the strings in a trie help?
Since the popularity of the chosen substring is the number of strings that have it as a prefix, then the chosen string should always be the prefix of some string. Consider putting all strings into a trie, such that each node represents a prefix of one or more of the given strings. The chosen string at the end should definitely be one of the nodes of the trie.
The popularity of a certain prefix can be found by keeping a count of the strings that passed through this node during insertion. This resolves the 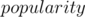 value of the node.
value of the node.
The length of the prefix is also easy to compute since it is equivalent to the depth of the node in the trie (the node's distance from the root). This resolves the 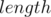 value of the node.
value of the node.
We are left with the last value which is 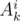 . If we get this value from the prefix of the string, we may end up with a wrong answer. Consider that the best substring to choose is
. If we get this value from the prefix of the string, we may end up with a wrong answer. Consider that the best substring to choose is 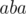 and it occurs in the string
and it occurs in the string  . If we take it as a prefix
. If we take it as a prefix  , we get a value of
, we get a value of 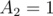 , but if we consider it as the other substring
, but if we consider it as the other substring 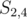 , we get a value of
, we get a value of 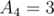 , which is better. How do we resolve that? Note that the other
, which is better. How do we resolve that? Note that the other 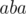 ,
, 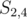 , is also part of a prefix of the string
, is also part of a prefix of the string 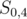 . So, we now have two substrings,
. So, we now have two substrings,  and
and 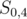 , where
, where  is a proper suffix of
is a proper suffix of 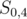 .
.
Recall how the Aho-Corasick algorithm for pattern matching constructs the trie and its suffix links (failure links). In the algorithm, every node (prefix) has a special edge pointing to a node (another prefix) which is the longest proper suffix of the first node. So, consider the maximum 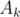 value for some node. We can push this value up through the suffix link to the other prefix node which is a proper suffix of the current one. Hence, we update the value of
value for some node. We can push this value up through the suffix link to the other prefix node which is a proper suffix of the current one. Hence, we update the value of 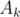 in the other node to make it the maximum of all possible values. By repeating this step in a bottom-up manner, we will have the maximum possible value of
in the other node to make it the maximum of all possible values. By repeating this step in a bottom-up manner, we will have the maximum possible value of 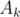 for the current substring stored in its node. Constructing these suffix link edges can be done in
for the current substring stored in its node. Constructing these suffix link edges can be done in 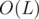 , where
, where 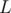 is the length of the strings (given that the alphabet is of finite size), and traversing the nodes through these links to push the joy level values can be done using regular
is the length of the strings (given that the alphabet is of finite size), and traversing the nodes through these links to push the joy level values can be done using regular 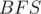 (note the topological sorting) on the nodes. In the worst case, the number of nodes in the trie will be equal to the total number of characters in the strings, which is at most
(note the topological sorting) on the nodes. In the worst case, the number of nodes in the trie will be equal to the total number of characters in the strings, which is at most 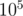 .
.
Now, every node, which is a prefix of some string, has stored in it the 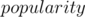 , the
, the 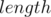 , and the maximum
, and the maximum 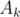 that it can have. All what is left is to traverse all the nodes and find which one has the highest quality. For every node, compute its quality and compare to a global maximum.
that it can have. All what is left is to traverse all the nodes and find which one has the highest quality. For every node, compute its quality and compare to a global maximum.
Complexity 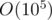
Deal with each cell individually.
Use the probability of flipping a single cell, to know its expected value at the end.
Since the flipping is done uniformly at random, we can deal with each cell separately. For every cell, we find its expected value after the 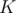 flips, and the final answer is the sum of expected values of all cells.
flips, and the final answer is the sum of expected values of all cells.
The expected value of a cell after flipping is the same as the probability of its value being one.
For every cell, we use a simple  , to calculate the probability of the cell having a value of
, to calculate the probability of the cell having a value of  after
after  flips. Then, the expected value of the cell at the end is
flips. Then, the expected value of the cell at the end is 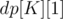 .
.
Initially, 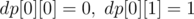 if the cell has value
if the cell has value  , and
, and 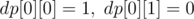 if the cell has value
if the cell has value  .
.
The probability of flipping a cell is equal to the number of submatrices containing this cell divided by the total number of submatrices.
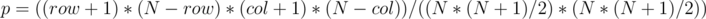 for
for 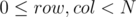

to get a value of  after
after  flips, we either get the probability of the cell being
flips, we either get the probability of the cell being  after
after  flips and don't flip the cell (probability
flips and don't flip the cell (probability  ), or get the probability of the cell being
), or get the probability of the cell being 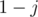 (not
(not  ) after
) after  flips and flip the cell (probability
flips and flip the cell (probability 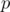 ).
).
For every cell, perform this 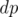 and add
and add 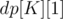 to the answer which is initially
to the answer which is initially  .
.
Complexity 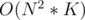
101991G - Greatest Chicken Dish
The queries can be answered offline.
Fix a starting point and consider all contiguous segments with this starting point. How many distinct GCD values are there?
First, let's define some handy structures. Let's create an array  which stores the logarithm base 2 of integers
which stores the logarithm base 2 of integers 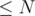 . Let's also create a sparse table on GCD so that we can find the GCD of all elements in a given interval
. Let's also create a sparse table on GCD so that we can find the GCD of all elements in a given interval  in constant time
in constant time 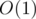 . The idea of a sparse table to store in
. The idea of a sparse table to store in  the GCD of all elements in the interval
the GCD of all elements in the interval 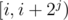 .
.  .
.
Since the queries are offline, it seems appropriate to apply MO's algorithm. The idea is to divide the interval 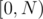 into blocks of size
into blocks of size 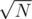 , so we sort the queries by
, so we sort the queries by 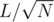 and then by
and then by 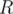 if they happen to be in the same block. Review MO's algorithm for a better understanding of the solution.
if they happen to be in the same block. Review MO's algorithm for a better understanding of the solution.
Now, if we have the solution for a certain interval, we can loop on the queries in the sorted order and answer them all in 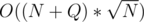 . The answer is the number of segments in the interval
. The answer is the number of segments in the interval  that have GCD
that have GCD  . Since the value of
. Since the value of  changes among queries, the answer should be stored in an array. Let's define
changes among queries, the answer should be stored in an array. Let's define 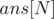 that stores, for every value
that stores, for every value 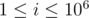 the number of segments in
the number of segments in 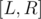 with GCD equal to
with GCD equal to  . Therefore, the answer to a particular query is
. Therefore, the answer to a particular query is 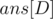 .
.
How will we do the editing of the 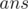 array as we move the interval's starting and ending points? First, notice an important property. Consider all the segments starting at index
array as we move the interval's starting and ending points? First, notice an important property. Consider all the segments starting at index  . Initially, the GCD is
. Initially, the GCD is 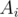 . As we the ending of the interval to right, the GCD can either stay the same or be divided by some integer greater than or equal to 2. So, there cannot be more than
. As we the ending of the interval to right, the GCD can either stay the same or be divided by some integer greater than or equal to 2. So, there cannot be more than 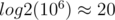 distinct GCD values for segments starting at a given index. This is extremely useful. For every index
distinct GCD values for segments starting at a given index. This is extremely useful. For every index  , we can store the distinct GCD values of segments starting at
, we can store the distinct GCD values of segments starting at  , with the ending index at which these GCDs start appearing. The first GCD is
, with the ending index at which these GCDs start appearing. The first GCD is 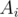 and it starts appearing at is
and it starts appearing at is  . We can perform a binary search to find the max index at which the GCD remains the same (remember the useful sparse table we created), or we can just walk on powers of two from greatest to least and add to the index as long as there is no change in GCD value. Repeat the same procedure, but now fix the right end of the interval and consider segments ending at a fixed index. Now, we have two arrays of maps or two arrays of vectors containing pairs (the GCD and the index).
. We can perform a binary search to find the max index at which the GCD remains the same (remember the useful sparse table we created), or we can just walk on powers of two from greatest to least and add to the index as long as there is no change in GCD value. Repeat the same procedure, but now fix the right end of the interval and consider segments ending at a fixed index. Now, we have two arrays of maps or two arrays of vectors containing pairs (the GCD and the index).
Back to MO's algorithm, when we decrement 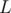 , check the array of GCDs starting at
, check the array of GCDs starting at 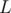 . Loop on this array and, for every GCD value, add to the
. Loop on this array and, for every GCD value, add to the 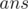 array, the number of segments starting at
array, the number of segments starting at 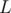 and having this GCD. This count can be obtained by subtracting the index of appearance of the next GCD value from the index of appearance of the current GCD value. However, note that we should not exceed the
and having this GCD. This count can be obtained by subtracting the index of appearance of the next GCD value from the index of appearance of the current GCD value. However, note that we should not exceed the 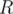 value that we have since we will be counting segments that should not be in the solution. The same goes for incrementing
value that we have since we will be counting segments that should not be in the solution. The same goes for incrementing 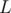 , but this time we subtract the number of segments from the
, but this time we subtract the number of segments from the 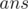 array. And for incrementing or decrementing
array. And for incrementing or decrementing 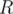 , we follow the same steps but using the other array where we fixed the ending point and varied the starting point.
, we follow the same steps but using the other array where we fixed the ending point and varied the starting point.
Now, we can increment and decrement the interval in  , and all we need to do is to go over the queries as we sorted them and store their answers. Print the answer of the queries in the order that the queries were given in the input.
, and all we need to do is to go over the queries as we sorted them and store their answers. Print the answer of the queries in the order that the queries were given in the input.
Complexity 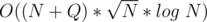
Can you try all values of 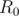 ?
?
Write the term 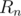 in terms of
in terms of  .
.
The first thing to notice is that the interval  is of size at most
is of size at most 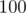 , so we can try all possibilities for
, so we can try all possibilities for 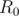 . So, for every
. So, for every 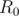 , we check if we can reach the value
, we check if we can reach the value 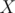 . The final answer is the number of seed values that satisfy the required condition, divided by the total number of seed values.
. The final answer is the number of seed values that satisfy the required condition, divided by the total number of seed values.
The next step is to write 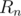 in terms of
in terms of  and
and 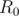 only and not as a recurrence.
only and not as a recurrence.



We want 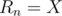 , so substitute it in the equation
, so substitute it in the equation
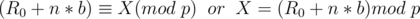

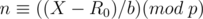
In this case,  can be computed through modular inverse and multiplication.
can be computed through modular inverse and multiplication.
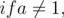
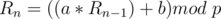


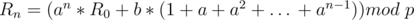
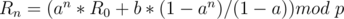
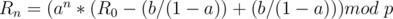
Let's discuss another special case
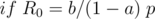
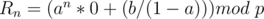
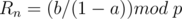
In this case, 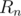 is a constant, so just check if this constant is equal to
is a constant, so just check if this constant is equal to 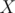 .
.
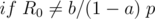
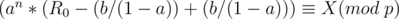
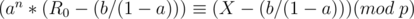
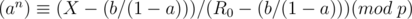
We want an integer  such that
such that 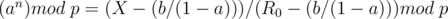 . This is known as the discrete logarithm and can be found in
. This is known as the discrete logarithm and can be found in 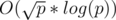 .
.
Let the right hand side of the congruence above be  , so we have
, so we have 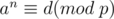
Let 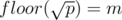 and write
and write 
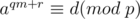
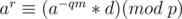
Now, loop on all possible values of 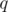 and compute the corresponding
and compute the corresponding  . Looping on
. Looping on 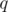 can be done in
can be done in  , but how can we know the corresponding
, but how can we know the corresponding  ? Preprocessing! Previously, general all possible values of
? Preprocessing! Previously, general all possible values of 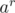 also in
also in  , and sort by
, and sort by 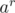 while maintaining the corresponding value of
while maintaining the corresponding value of  . (This can be done using pairs in C++ or even using a map) (we care about min value only). So, loop on all values of
. (This can be done using pairs in C++ or even using a map) (we care about min value only). So, loop on all values of 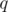 , compute
, compute 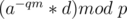 , then perform a binary search (or a map search) on the values of
, then perform a binary search (or a map search) on the values of 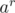 to find the corresponding
to find the corresponding  . After this
. After this 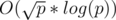 algorithm, we can know if there exists an integer
algorithm, we can know if there exists an integer  such that
such that 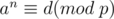 and this will be the
and this will be the  such that
such that 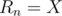 .
.
A quick recap on the solution, first loop on all values of 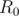 and check if each of them gives a value of
and check if each of them gives a value of 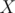 among the first
among the first 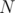 terms of the sequence. Deal with the special cases or apply the algorithm discussed above for each
terms of the sequence. Deal with the special cases or apply the algorithm discussed above for each 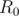 . The final answer is the number of
. The final answer is the number of 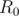 values that give
values that give 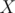 divided by the total number of
divided by the total number of 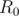 values. Note that all operations are done
values. Note that all operations are done 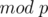 , including exponentiation, multiplication, division (inverse). Also, remember to check if the found value is within the limits
, including exponentiation, multiplication, division (inverse). Also, remember to check if the found value is within the limits  .
.
Complexity 
What is the calorie value of the densest ice-cream chosen?
Given the value of the above value of calories, how do we maximize the happiness?
The first thing we will find is the calorie value of the densest chosen ice-cream. Since we want to minimize this value, then it is optimal to consider the ice-creams in increasing order of calorie value. Then, the minimum value we can get as a result is the calories of the  ice-cream. Taking any other combination besides the
ice-cream. Taking any other combination besides the 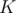 first terms in the sorted array will give an answer that is at least as large as the one we found. Now that we have resolved the first output value, we want to maximize the total happiness, so we find all ice-creams that have calorie value less than or equal to the max calorie value found before (not just the first
first terms in the sorted array will give an answer that is at least as large as the one we found. Now that we have resolved the first output value, we want to maximize the total happiness, so we find all ice-creams that have calorie value less than or equal to the max calorie value found before (not just the first 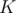 ice-creams). Out of these ice-creams, we want to pick the best (most happiness), so we sort them in decreasing order of happiness and take the first
ice-creams). Out of these ice-creams, we want to pick the best (most happiness), so we sort them in decreasing order of happiness and take the first 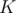 . Also, this guarantees the maximum happiness that we can get.
. Also, this guarantees the maximum happiness that we can get.
Complexity 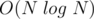
Do we need the numbers themselves or only 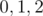 ?
?
Is it easier to calculate the count of partial (prefix) sum arrays instead of the number of arrays?
The first thing to observe is the the numbers themselves don't matter. What matters is the remainder of the number by 3, so we can limit our work to the elements 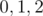 only.
only.
We usually find the sum of an interval 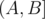 in an array by constructing the prefix sum array and computing
in an array by constructing the prefix sum array and computing 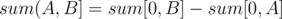 . Let's apply this on the problem at hand. If we want the sum
. Let's apply this on the problem at hand. If we want the sum 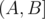 to be divisible by 3, then
to be divisible by 3, then 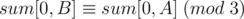 (they have the same remainder when divided by 3. If we consider the prefix sum array as consisting of only zeroes, ones, and twos (the remainder of the sum by 3 instead of the sum itself), then we can get the number of sub-arrays of sum divisible by 3 simply by picking 2 ones or 2 twos or 2 threes (since subtracting the two will give a sum divisible by 3). Also, picking a zero alone will give a sum divisible by 3. So, if we have the prefix sum array with the remainders of sums by 3 instead of the sums themselves, we the number of sub-arrays of sum divisible by 3 is
(they have the same remainder when divided by 3. If we consider the prefix sum array as consisting of only zeroes, ones, and twos (the remainder of the sum by 3 instead of the sum itself), then we can get the number of sub-arrays of sum divisible by 3 simply by picking 2 ones or 2 twos or 2 threes (since subtracting the two will give a sum divisible by 3). Also, picking a zero alone will give a sum divisible by 3. So, if we have the prefix sum array with the remainders of sums by 3 instead of the sums themselves, we the number of sub-arrays of sum divisible by 3 is
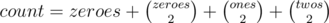 where
where  are the number of zeroes, ones, and twos in the prefix sum array.
are the number of zeroes, ones, and twos in the prefix sum array.
Also, note that 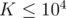 and
and 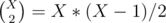 . For
. For 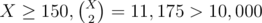 . Therefore, the number of zeroes, ones, and twos cannot exceed 150 each or else we cannot find exactly
. Therefore, the number of zeroes, ones, and twos cannot exceed 150 each or else we cannot find exactly 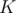 sub-arrays (but much more).
sub-arrays (but much more).
For every possible value of zeroes, ones, and twos (3 nested loops, each from 0 to 150), if they give us exactly 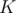 (based on the formula above), then we add to the answer the number of ways we can make a prefix sum array having this many zeroes, ones, and twos.
(based on the formula above), then we add to the answer the number of ways we can make a prefix sum array having this many zeroes, ones, and twos.
To count the number of prefix sum arrays that have a certain number of zeroes, ones, and twos, we use a simple 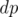 . Solve all values of this
. Solve all values of this 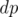 before doing the looping discussed above.
before doing the looping discussed above.
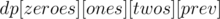 , where
, where  are the number of zeroes, ones, twos placed or remaining (in the range
are the number of zeroes, ones, twos placed or remaining (in the range 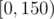 and
and 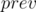 is the previous sum found (previous element) in the range
is the previous sum found (previous element) in the range 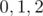
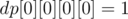 initially since adding no elements means a sum of 0, and all other values of
initially since adding no elements means a sum of 0, and all other values of 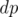 are 0. Filling the
are 0. Filling the 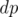 is straight-forward since we can add a number whose remainder by 3 is 0, 1, or 2 to make the new prefix sum with remainder 0, 1, or 2 by 3.
is straight-forward since we can add a number whose remainder by 3 is 0, 1, or 2 to make the new prefix sum with remainder 0, 1, or 2 by 3.
The number of elements 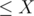 that give a remainder
that give a remainder 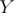 when divided by
when divided by  is
is 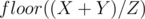 , so the number of elements in the range
, so the number of elements in the range 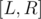 that give a remainder
that give a remainder  when divided by
when divided by  is
is 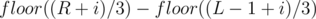
Complexity 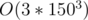
Note the constraint 
Note the constraint 
Consider this approach, for every bit position 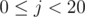 , find any element
, find any element 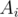 with the
with the  bit set, and include it in the solution set. This guarantees that the final answer will have the
bit set, and include it in the solution set. This guarantees that the final answer will have the  bit set. Since
bit set. Since 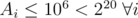 , then we will not include more than
, then we will not include more than 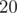 elements in the solution set. Also, since
elements in the solution set. Also, since  , then this strategy works for any given value of
, then this strategy works for any given value of 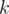 . Hence, we have an
. Hence, we have an 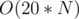 algorithm if we loop on all elements for every bit position.
algorithm if we loop on all elements for every bit position.
However, if we examine the above operation, we are setting the  bit in the final answer if there is at least one element
bit in the final answer if there is at least one element 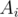 with the
with the  bit set. This is the same as the bitwise
bit set. This is the same as the bitwise 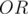 operation on all elements. So, all we need is to loop on all elements and compute
operation on all elements. So, all we need is to loop on all elements and compute  and this will be the answer to print.
and this will be the answer to print.
Complexity 










