In this comment, it's mentioned that the complexity of __builtin__popcount for any integer j with j = O(2N) is O(N) (i.e 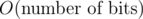 ) instead of O(1). So to count the number of one in a large binary string of length n with n > > 64, if I split n into
) instead of O(1). So to count the number of one in a large binary string of length n with n > > 64, if I split n into 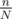 substrings (with N = 64 / 32 / 16) and apply builtin popcount to each of the substrings and add them up, then the total time complexity should be
substrings (with N = 64 / 32 / 16) and apply builtin popcount to each of the substrings and add them up, then the total time complexity should be 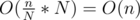 instead of
instead of 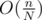 .
.
But in page 101 of Competitive programmers handbook on the topic Counting Subgrids, based on the time taken to compute the results, the time should be same no matter if N = 64 for N = 32. But it turns out that they're different as "the bit optimized version only took 3.1 seconds with N = 32 (int numbers) and 1.7 seconds with N = 64 (long long numbers)".
Why N = 64 takes less time ?










