Given an undirected graph with integer edge labels and two nodes u and v, is it possible to calculate efficiently whether there's a simple path between u and v such that all labels are unique?
| # | User | Rating |
|---|---|---|
| 1 | ecnerwala | 3649 |
| 2 | Benq | 3581 |
| 3 | orzdevinwang | 3570 |
| 4 | Geothermal | 3569 |
| 4 | cnnfls_csy | 3569 |
| 6 | tourist | 3565 |
| 7 | maroonrk | 3531 |
| 8 | Radewoosh | 3521 |
| 9 | Um_nik | 3482 |
| 10 | jiangly | 3468 |
| # | User | Contrib. |
|---|---|---|
| 1 | maomao90 | 174 |
| 2 | awoo | 164 |
| 3 | adamant | 161 |
| 4 | TheScrasse | 159 |
| 5 | nor | 158 |
| 6 | maroonrk | 156 |
| 7 | -is-this-fft- | 151 |
| 8 | SecondThread | 147 |
| 9 | orz | 146 |
| 10 | pajenegod | 145 |
Perhaps offtopic for Codeforces, but anyway: does anyone know of a mathematical logic interest group in Minsk or elsewhere in Belarus? Or whether some of the universities (BSU and others) have a strong mathematical logic department?
By mathematical logic, I mean it in its formal sense: proof theory, model theory, recursion theory, set theory, etc.
Thanks.
I noticed there are a few books (in Russian) specific to competitive programming in e-maxx. For example, Олимпиадные задачи по программированию by Меньшиков; the CD with materials is also available and the tasks are also hosted in acmp.ru. However, the book is rather old.
Are these books actually popular in the Russian-speaking community? What about the tasks' quality? How do they compare to more modern English-language alternatives, such as pllk's book and Competitive Programming?
After solving tasks, how to know which ones are solved already? (besides checking the "Submissions" tab)
I could not find it but, is there a view that lists the tasks highlighting the ones you already solved?
Thanks!
Consider the following problem:
We are given N sets {S1, ..., SN} of integers, with 1 ≤ |Si| ≤ 16 (i.e. no set is empty or has more than 16 elements) and 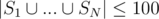 . We want to partition the given sets into the minimum number of partitions such that the number of elements in the union of all sets in any partition doesn't exceed given constant K ≤ 16.
. We want to partition the given sets into the minimum number of partitions such that the number of elements in the union of all sets in any partition doesn't exceed given constant K ≤ 16.
Is there a way to sort the sets such that the partitions of the optimal solution are contiguous? (in which case a DP solution to the original problem follows). How to prove such properties for other partition cost functions in general?
Thanks!
P.S.: I found this: https://books.google.co.uk/books?id=PD3ICgAAQBAJ&pg=PA293&lpg=PA293&dq=Partition+Problems+over+Single-Parameter+Spaces:+Combinatorial+Approach&source=bl&ots=FdNvNpE_96&sig=MQOnuezKZfMUbyACjqZq5adR_rM&hl=en&sa=X&ved=0ahUKEwjrj67K7qTZAhVkJMAKHXW0APIQ6AEILjAA#v=onepage&q&f=false but unfortunately is not available in full.
Is there a way to know which topcoder problems you already solved in practice mode? I mean, an easy way, in the same fashion you see it in any reasonable online judge, such that I can scroll and pick a problem that I still didn't solve.
Thanks!
Hi folks :)
I wanted to learn a bit of golang. Being a CHelper user, I decided to code a tool focused on golang, although much more limited of course. Maybe others will find it useful, so here it is!
Wouldn't it be awesome to be able to rate the quality of problems? Then you could sort the problem set by quality, where I define "quality" of a problem as having some (or all) of the following properties:
- the statement is not long and boring and irrelevant
- the solution is not evident
- the solution involves some interesting insights
- the implementation involves some tricks that might prove useful for other problems
- the tests are properly crafted to avoid flaky/lucky solutions to pass
- whatever else you might consider
Before the hordes of trolls and Xellos take care of this post, I want to state my awareness that quality is quite subjective and the aforementioned trolls may as well jeopardize this rating. Still, I trust the community and I believe this idea would be helpful for many people. I would love to hear your opinions!
I have been experimenting with Kotlin lately, and it's a very simple and comfortable alternative to Java (at least in the scope of programming contests, I cannot find a case where some solution written in Kotlin would be uglier than the Java equivalent). Moreover, Codeforces supports Scala, which also runs on JVM, it's a much more expressive language with more advanced features, although they are useless for the competitive programming context: thus is makes more sense to add Kotlin (also|instead).
I would like to know what people think about it, and if I can contribute anyhow to make it possible, I would like to know as well. Thanks!
Is this problem solvable with some data structure or some other idea is required?
You have M sets of N-bit strings, numbered from 1 to M, and all of them are initially empty. Then, you have Q operations of the following kind: add to the i-th set, all the N-bit strings with the k-th bit equal to b. You must output the number of N-bit strings in the set consisting of the intersection of all the M sets after adding all the strings.
Input
The first line of input consists of 3 positive integers: M (2 ≤ M ≤ 100000), N (1 ≤ N ≤ 10000) and Q (0 ≤ Q ≤ 100000). The next Q lines consists each of 3 integers: i (1 ≤ i ≤ M), k (0 ≤ k < N) and b (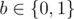 ), representing the operation described above in the statement.
), representing the operation described above in the statement.
Output
One line with one integer. The number of strings in the intersection of the M sets after all the operations. It is guaranteed that the answer will fit in a 32 bit signed integer.
Example input
3 3 3
1 0 1
3 2 1
2 1 0
Example output
1
Explanation
There are 3 initial empty sets of 3-bit strings. There are 3 operations. The first one adds to the first set all the strings with the bit 0 equal to 1. The second one adds to the third set all the strings with the bit 2 equal to 1. The third one adds to the second set all the strings with the bit 1 equal to 0. So, after all the operations, the sets consists of the following strings:
1) {100, 101, 110, 111}
2) {000, 001, 100, 101}
3) {001, 011, 101, 111}
The intersection of the 3 sets is the set {101}, so the answer is 1.
Thanks!
Hi. Today competitive programmers certainly have a lot of online resources to practice. Nevertheless, there are so many problems out there, that it's hard to find some "valuable" problem sometimes. By "valuable", I mean a problem that is not just some repeated-idea problem or some problem that the participant already encountered before, or maybe just some problem that provides no new knowledge or it's too long/boring to be worthy to practice, since you will expend more time reading/understanding/coding the problem in relation to what you really learn from it. So, I would like everyone interested to post a small (or big?) list of problems that he/she considers VERY valuable so far in his/her practice so far. If people like the idea, we can later collect this information and compile some nice list of "The Most Valuable Practice Problems" or something similar. Thanks for reading and looking forward to hear the opinion from the community!
| Name |
|---|










