If n is even, then the answer is n / 2, otherwise the answer is (n - 1) / 2 - n = - (n + 1) / 2.
Hint of this problem is presented in its statement. "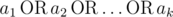 where
where 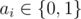 is equal to 1 if some ai = 1, otherwise it is equal to 0."
is equal to 1 if some ai = 1, otherwise it is equal to 0."
To solve this problem, do 3 following steps:
- Assign all aij (1 ≤ i ≤ m, 1 ≤ j ≤ n) equals to 1.
- If some bij = 0, then do assignments: aik = atj = 0 (1 ≤ k ≤ n, 1 ≤ t ≤ m) (that means, assign all elements in row i and column j of matrix a to 0).
- Then we have matrix a which need to find. Just check whether from matrix a, can we produce matrix b. If not, the answer is obviously "NO".
Complexity: We can implement this algorithm in O(m * n), but it's not neccesary since 1 ≤ m, n ≤ 100.
486C - Palindrome Transformation
Assuming that cursor's position is in the first half of string(i.e 1 ≤ p ≤ n / 2) (if it's not, just reverse the string, and change p to n - p + 1, then the answer will not change).
It is not hard to see that, in optimal solution, we only need to move our cusor in the first half of the string only, and the number of "turn" is at most once.
Therefore, we have below algorithm:
Find the largest index r before p in the first half of the string (p ≤ r ≤ n / 2) such that sr different to sn - r + 1. (si denote ith character of our input string s)
Find the smallest index l after p (1 ≤ l ≤ p) such that sl different to sn - l + 1.
In optimal solution, we move our cusor from p to l and then from l to r, or move from p to r and then from r to l. While moving, we also change character of string simultaneously (if needed) (by press up/down arrow keys).
Be careful with some corner case(for example, does'nt exist such l or r discribed above).
Complexity: O(n).
Firstly, we solve the case d = + ∞. In this case, we can forget all ai since they doesn't play a role anymore. Consider the tree is rooted at node 1. Let Fi be the number of valid sets contain node i and several other nodes in subtree of i ("several" here means 0 or more). We can easily calculate Fi through Fj where j is directed child node of i:
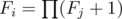 . Complexity: O(n).
. Complexity: O(n).General case: d ≥ 0. For each node i, we count the number of valid sets contain node i and some other node j such that ai ≤ aj ≤ ai + d (that means, node i have the smallest value a in the set). How? Start DFS from node i, visit only nodes j such that ai ≤ aj ≤ ai + d. Then all nodes have visited form another tree. Just apply case d = + ∞ for this new tree. We have to count n times, each time take O(n), so the overall complexity is O(n2). (Be craeful with duplicate counting)
Here is my code.
LIS = Longest increasing subsequence.
Solution 1 (Most of participant's solutions):
- Let F1i be the length of LIS ending exactly at ai of sequence {a1, a2, ..., ai} and D1i is the number of such that LIS.
- Let F2i be the length of LIS beginning exactly at ai of sequence {ai, ai + 1, ..., an} and D2i is the number of such that LIS.
// Calculates F1i and F2i is familiar task, so I will not dig into this. For those who have'nt known it yet, this link may be useful)
// We can calculate D1i and D2i by using advanced data structure, like BIT or Segment tree.
l = length of LIS of {a1, a2, ..., an} = max{F1i} = max{F2j}.
m = number of LIS of {a1, a2, ..., an} =

Let Ci be the number of LIS of {a1, a2, ..., an} that ai belongs to. Index i must in group:
1) if Ci = 0
2) if 0 ≤ Ci < m
3) if Ci = m
How to calculate Ci? If (F1i + F2i - 1 < l) then Ci = 0, else Ci = D1i * D2i. Done!
We have an additional issue. The number of LIS of {a1, a2, ..., an} maybe very large! D1i, D2i and m maybe exceed 64-bits integer. Hence, we need to store D1i, D2i and m after modulo some integer number, call it p.
Usually, we will choose p is a prime, like 109 + 7 or 109 + 9. It's not hard to generate a test such that if you choose p = 109 + 7 or p = 109 + 9, your solution will lead to Wrong answer. But I have romeved such that tests, because the data tests is weak, even p is not a prime can pass all tests.
Solution 2:
// Some notation is re-defined.
Let F1i be the length of LIS ending exactly at ai of sequence {a1, a2, ..., ai}.
Let F2i be the length of LIS beginning exactly at ai of sequence {ai, ai + 1, ..., an}.
l = length of LIS of {a1, a2, ..., an} = max{F1i} = max{F2j}.
Let Fi be the length of LIS of sequence {a1, a2, ..., ai - 1, ai + 1, ..., an} (i.e the length of LIS of initial sequence a after removing element ai).
Index i must in group:
1) if F1i + F2i - 1 < l, otherwise:
2) if Fi = l
3) if Fi = l - 1
How to caculate Fi? We have: Fi = max{F1u + F2v} among 1 ≤ u < i < v ≤ n such that au < av. From this formula, we can use Segment tree to calculate Fi. Due to limitation of my English, it is really hard to write exactly how. I will post my code soon.
Complexity of both above solution: O(nlogn).









