How can I write math in my blog now? The old functionality (using dollar signs) no longer seems to work, e.g.
a = b + c
Update: It's fixed :)
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
How can I write math in my blog now? The old functionality (using dollar signs) no longer seems to work, e.g.
a = b + c
Update: It's fixed :)
This post is motivated by a problem I recently saw, Problem G of NCPC 2007. This is a standard problem that I'm sure many of you have seen before, but the general topic of partially ordered sets is not too well known.
Let S be a set of elements and ≤ be a partial ordering on the set. That is, for some elements x and y in S we may have x ≤ y. The only properties that ≤ must satisfy are reflexivity (x ≤ x), antisymmetry (if x ≤ y and y ≤ x, then x = y), and transitivity (if x ≤ y and y ≤ z, then x ≤ z). Note that because it is a partial ordering, not all x and y are comparable.
An example of a partially ordered set (poset) is the set of points (x, y) in the Cartesian plane with the operator (x1, y1) ≤ (x2, y2) iff x1 ≤ x2 and y1 ≤ y2 (e.g. NCPC 2007 problem).
We define a chain C to be a subset of S such that the elements of C can be labelled x1, x2, ..., xn such that x1 ≤ x2 ≤ ... ≤ xn. A partition P is a set of chains where each element 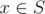 occurs in exactly one chain.
occurs in exactly one chain.
We define an antichain A to be a subset of S such that for any x and y in A we have neither x ≤ y nor y ≤ x. That is, no two elements of an antichain are comparable.
We can define the width of a poset in two ways, which is the result of Dilworth's Theorem. One definition is the size of the maximum antichain; the other is the size of the minimum partition. It is easy to see that any partition must have at least as many chains as the size of the maximum antichain because every element of the antichain must be in a different chain. Dilworth's Theorem tells us that there exists a partition of exactly that size and can be proved inductively (see Wikipedia for proof).
So how does one calculate the width of a poset? To solve this problem in general, we can use maximum matching on a bipartite graph. Duplicate each element x in S as ux and vx and if x ≤ y (for x ≠ y) then add the edge 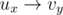 . If you compute the maximum matching on this graph, this is equivalent to partitioning the elements into chains, where if the edge
. If you compute the maximum matching on this graph, this is equivalent to partitioning the elements into chains, where if the edge 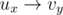 is chosen then x and y are in the same chain. In particular, if the size of the matching is m and |S| = n, then the number of partitions is n - m. Notice that this gives a bijection between partitions and matchings, so the maximum matching gives the minimum partition, which we know is equal to the width as given by Dilworth's Theorem.
is chosen then x and y are in the same chain. In particular, if the size of the matching is m and |S| = n, then the number of partitions is n - m. Notice that this gives a bijection between partitions and matchings, so the maximum matching gives the minimum partition, which we know is equal to the width as given by Dilworth's Theorem.
So now that we can calculate the width of a poset, we can just apply that to our problem, right? Not quite.
The bounds on our problem are up to 20, 000 so we can't use maximum matching. Luckily, points in the Cartesian plane are more structured than general posets, and we can use the other definition of width (maximum antichain) to solve this problem more efficiently. Consider iterating over the points sorted in order by x. We maintain a set of pairs (a, b) which indicates that there is an antichain of size b that ends at y-value a (among all points that have already been processed). Thus for any future point (x, y) we can insert (y, b + 1) into the set as long as y < a.
Notice, however, that if we have two points in the set (a, b) and (c, d) such that c ≤ a and d ≤ b then the latter is redundant (it is always worse) and we can remove it. In this way we keep the set small and only need to check a single element whenever we insert, which is (a, b) with minimal a such that a > y. All of this can be done with a C++ set, for example. At the end, the largest antichain we recorded is indeed the maximum one, and we are done.
A recent Google Code Jam problem uses these ideas.
Hey everyone,
It's been some time since my last blog post, so this is the first one of the new year. Although I didn't participate in Round 102, I worked through several of the problems, and this post is motivated by Problem D. It is about a variation on our favorite algorithmic game, Nim. There is already an editorial for the round, but I intend to use this post as future reference in case I come upon such problems again. If you don't see the reduction from the problem to the Nim variation, please read the editorial.
 , where
, where  is the XOR operator. To prove this, we simply realize that from any losing position, if we change the value of one pile, the XOR will no longer be zero (thus a winning position). And from any winning position, we can look at the highest order bit which does not XOR to zero, pick a pile in which that bit is 1, change it to 0, and adjust the rest of the bits in that pile to make the XOR zero.
is the XOR operator. To prove this, we simply realize that from any losing position, if we change the value of one pile, the XOR will no longer be zero (thus a winning position). And from any winning position, we can look at the highest order bit which does not XOR to zero, pick a pile in which that bit is 1, change it to 0, and adjust the rest of the bits in that pile to make the XOR zero. .
. is all zeros. The proof of this result is a little less nice, so I will just outline the idea. From any losing position, consider the highest order bit affected among any of the piles. This bit always goes from 1 to 0 (or else the pile is getting bigger). Since at most k piles are affected, the (k + 1)-XOR of that bit can no longer be 0, leaving us in a winning position.
is all zeros. The proof of this result is a little less nice, so I will just outline the idea. From any losing position, consider the highest order bit affected among any of the piles. This bit always goes from 1 to 0 (or else the pile is getting bigger). Since at most k piles are affected, the (k + 1)-XOR of that bit can no longer be 0, leaving us in a winning position.void init() {
for (int x = 0; x < N; x++)
t[x][0] = a[x];
for (int y = 1; y <= n; y++)
for (int x = 0; x < N; x+=(1<<y))
t[x][y] = f(t[x][y-1], t[x+(1<<(y-1))][y-1]);
}
void set(int x, int v) {
t[x][0] = a[x] = v;
for (int y = 1; y <= n; y++) {
int xx = x-(x&((1<<y)-1));
t[xx][y] = f(t[xx][y-1], t[xx+(1<<(y-1))][y-1]);
}
}
int get(int i, int j) {
int res = IDENTITY, h = 0; j++;
while (i+(1<<h) <= j) {
while ((i&((1<<(h+1))-1)) == 0 && i+(1<<(h+1)) <= j) h++;
res = f(res, t[i][h]);
i += (1<<h);
}
while (i < j) {
while (i+(1<<h) > j) h--;
res = f(res, t[i][h]);
i += (1<<h);
}
return res;
}
Today I have become one :D
This was a pretty good SRM for me, tantalizingly close to red now. I'll talk about the easy (decent) and medium (really cool), but I didn't have time to take a look at the hard.
int a[100100], c[100100];
int main() {
int n; cin >> n;
for (int i = 0; i < n; i++) cin >> a[i];
sort(a, a+n);
int m = a[n-1]-a[0];
if (n % 2 == 1 || m > n/2 || m == 0) { cout << "NO" << endl; return 0; }
memset(c, 0, sizeof(c));
for (int i = 0; i < n; i++) c[a[i]-a[0]]++;
bool poss = true;
int L = c[0]-1;
for (int i = 1; i < m; i++) {
if (c[i] < L+2) { poss = false; break; }
c[i] -= (L+2); L = c[i];
}
poss = poss && (c[m] == L+1);
cout << (poss ? "YES" : "NO") << endl;
return 0;
}In my quest to regain my red color on Topcoder this morning, I failed once again in SRM 523. I'll present a quick summary of the solutions here; the problem set was actually quite easy, but with some tricks and edge cases.
int L = 0, R = 0;
for (int i = 1; i < n; i++) {
if (i > R) {
L = R = i;
while (R < n && s[R-L] == s[R]) R++;
z[i] = R-L; R--;
} else {
int k = i-L;
if (z[k] < R-i+1) z[i] = z[k];
else {
L = i;
while (R < n && s[R-L] == s[R]) R++;
z[i] = R-L; R--;
}
}
}int maxz = 0, res = 0;
for (int i = 1; i < n; i++) {
if (z[i] == n-i && maxz >= n-i) { res = n-i; break; }
maxz = max(maxz, z[i]);
}| Name |
|---|


