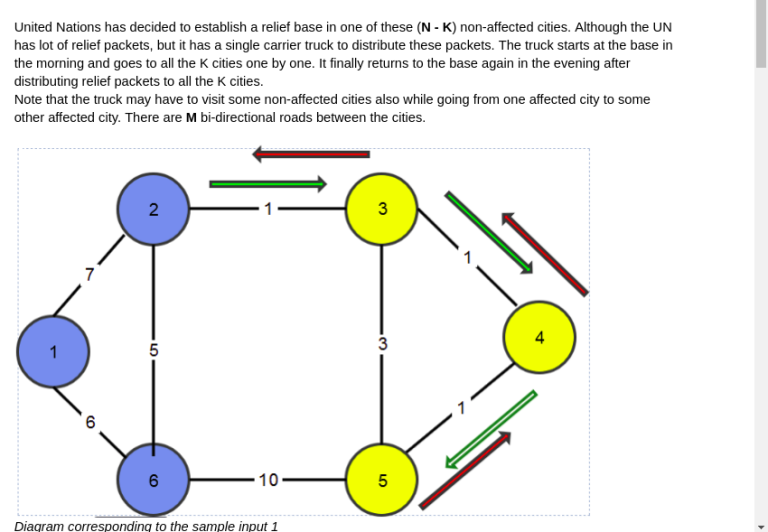

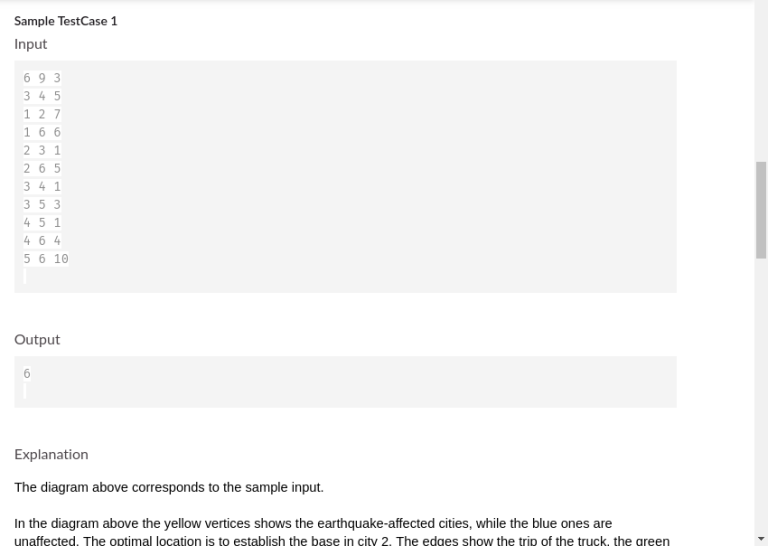
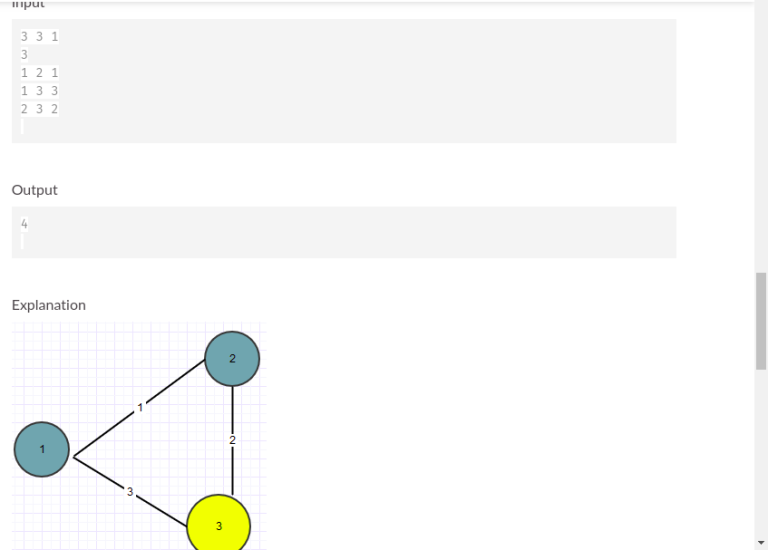
As the round is over, the links are disabled by them.
I can only come up with a very basic brute force solution of $$$(2*N)!$$$ where for each of the order of visiting I calculate the cost and then update the answer accordingly. But as expected this even didn't pass even a single test.
Can someone please help me with some spoilers on how to proceed further with it?
Thanks!
Edit: Hello all! Why everyone is downvoting the post? Is there something wrong with it or I asked the question in a wrong way ? I find the problem difficult so I asked for help and if someone find it easy then instead of directly downvoting please explain the solution (or atleast a step towards it) and then downvote if you think it's irrelevant.










