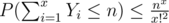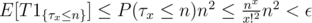Additional explanation of the solution, requested by ehsanoo. On the contrary to the tutorial, we will apply the queries online (however result itself will be calculated offline anyway; after you understand this part, you can revert the construction to obtain the solution described in the tutorial). We will keep our string in a compressed form of a DAG.
- The DAG on the left represents the string from the first sample test: 123123. Note that the root consists of 6 cells. Each represents a digit of 123123, however their values are not stored there. Each cell points to the leaf corresponding to its content. Note that cells corresponding to the same digit point to the same leaf.
- Now the first query comes: 2->00, so our string should become 10031003. What we do? We grab our leaf '2' and replace it with a new node (with 2 cells pointing to 0). Everything what was pointing to '2' now points to our new node (i.e. we replaced all occurrences of '2').
- Note that we create a new leaf '2' (marked as red). In general case the replacing string can contain the digit which is being replaced and we don't want the node to point to itself (i.e. we are not doing a recursive replacement).
To sum up: every node of the DAG represents some substring of the current string. At any point of processing the queries, we keep track of nodes which correspond to the single digits, so that we can replace them with a string from a query. For the replaced digit we create a new node and from now on, any new occurrences of this digit should point to this new node. At any point we can retrieve the current string by traversing the DAG. After processing all the queries we want to retrieve the result. To do that, we can dynamically calculate 2 values for each node:
- the number it represents mod (109 + 7)
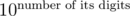 mod (109 + 7)
mod (109 + 7)
It is easy to see how to calculate them for the parent, if we already calculated them for the children.









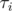 . Then
. Then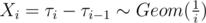 independent
independent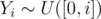 independent
independent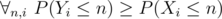
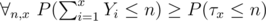
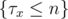 is exactly an event in which we eventually obtain a weapon of level
is exactly an event in which we eventually obtain a weapon of level 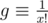 in lebesgue measure. It is easy to see that
in lebesgue measure. It is easy to see that 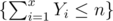 is contained in a hypercone of lebesgue volume
is contained in a hypercone of lebesgue volume 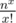 . By taking into consideration the density
. By taking into consideration the density