Hello Codeforcers!
I'd like to demonstrate an application of Extended Field. Sometimes a problem may be easier to solve if a (hidden or not) polynomial can be decomposed into product of linear terms. (Most of the time it's not the solution of tutorial.) In this case, we can try to extend the field to solve the problem.
Extended Field
The idea
First we should include the idea of splitting field, a splitting field F of a (may assumed) monic polynomial P is the smallest field such that
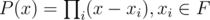
I use the word "smallest" with the sense that if P split over E, 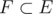 .
.
In the other word, P decomposes into linear factor under its splitting field.
In most of the problems, we need not to find the exact splitting field... Just a field that P split over it is enough.
Example
P = x2 + 1 does not split over
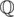 but split over
but split over  where
where 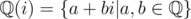 which is widely used as complex.
which is widely used as complex.Let p = 998244353 = 7 * 17 * 223 + 1, P = x224 - 1 does not split over
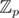 but split over
but split over 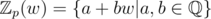 where
where 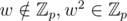 . The multiplication order ord(w2) = 223.
. The multiplication order ord(w2) = 223.Let p = 109 + 7, Fibonacci number can be easily written as
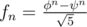 . where φ, ψ (the golden ratio and it's conjugate) are both root of x2 - x - 1 = 0. The splitting field is
. where φ, ψ (the golden ratio and it's conjugate) are both root of x2 - x - 1 = 0. The splitting field is 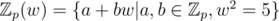 (Remark that x2 = 5 has no root in Zp)
(Remark that x2 = 5 has no root in Zp)
Problem Solving
718C - Sasha and Array
The problem to be demonstrated corresponds to the third example. This may be not the best solution for the problem. I've got several TL on this problem for large constant on module. But I do think that it's a nice try to solve some problems in different way :)
The problem contains several operations:
- shift all element of a segment to the next x Fibonacci term.
- query for the sum of an segment
In the problem, we can handle Fibonacci number 1, 1, 2, 3, 5, 8, ... with the formula 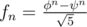 . Once we have decomposed the Fibonacci into two sequence of number powers. The problem becomes easier:
. Once we have decomposed the Fibonacci into two sequence of number powers. The problem becomes easier:
- multiply a segment by φx and ψx
- query for the sum of an segment
It can be easily handled by two segment tree.
Implementation
We can implement Extended Field using C++ class, just like complex:
template<int sq = 5, int MOD = 1000000007>
class EX {
int re, im;
static int trim(int a) {
if (a >= MOD) a -= MOD;
if (a < 0) a += MOD;
return a;
}
static int inv(const int a) {
int ans = 1;
for (int cur = a, p = MOD - 2; p; p >>= 1, cur = 1ll * cur * cur % MOD) {
if (p&1) ans = 1ll * ans * cur % MOD;
}
return ans;
};
public:
EX(int re = 0, int im = 0) : re(re), im(im) {}
EX& operator=(EX oth) { return re = oth.re, im = oth.im, *this; }
int norm() const {
return trim((1ll * re * re - 1ll * sq * im % MOD * im) % MOD);
}
EX conj() const {
return EX(re, trim(MOD - im));
}
EX operator*(EX oth) const {
return EX((1ll * re * oth.re + 1ll * sq * im % MOD * oth.im) % MOD,
(1ll * re * oth.im + 1ll * im * oth.re) % MOD);
};
EX operator/(int n) const {
return EX(1ll * re * inv(n) % MOD, 1ll * im * inv(n) % MOD);
}
EX operator/(EX oth) const { return *this * oth.conj() / oth.norm(); }
EX operator+(EX oth) const { return EX(trim(re + oth.re), trim(im + oth.im)); }
EX operator-(EX oth) const {
return EX(trim(re - oth.re), trim(im - oth.im));
}
EX pow(long long n) const {
EX ans(1);
for (EX a = *this; n; n >>= 1, a = a * a) {
if (n&1) ans = a * ans;
}
return ans;
}
bool operator==(EX oth) const { return re == oth.re and im == oth.im; }
bool operator!=(EX oth) const { return not (*this == oth); }
int real() const& { return re; }
int imag() const& { return im; }
};
My submission: 54522918
FFT
As the second example, since FFT need a root such that x2n - 1 = 0, the idea may be a nice approach for implementing FFT on arbitrary module. Yet I haven't found an efficient way to extend such arbitrary field  .
.










