Congratulations, Roman elizarov for being the first master filmed in a youtube advertisement!

| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
Congratulations, Roman elizarov for being the first master filmed in a youtube advertisement!

We'll consider problems of the kind "Find the probability $$$p$$$ of some event with the absolute error up to $$$\varepsilon$$$". One of the methods to solve it is the Monte Carlo method: we simulate this experiment $$$N$$$ times and estimate its probability as $$$\frac{number \ of \ successes}{N}$$$. Let's estimate the accuracy of this method.
Let $$$X_N$$$ be the random variable that denotes the result of running the experiment $$$N$$$ times; the probability of getting $$$\frac{k}{N}$$$ as the result is equal to $$$\binom{N}{k} p^k (1-p)^{N-k}$$$; in other words, it is equal to the binomial distribution divided by $$$N$$$. Its mean is $$$\mu = p$$$ and its standard deviation is $$$\sigma^2 = \frac{p(1-p)}{N}$$$.
According to Chebyshev's inequality:
We can bound $$$p(1-p)$$$ as $$$\frac{1}{4}$$$:
So if we want the probability of getting the wrong answer for a single test to be at most $$$0.05$$$, then we would like to run the experiment $$$5 \varepsilon^{-2}$$$ times, if possible; if we want the probability of getting the wrong answer for a single test to be at most $$$0.01$$$, then we would like to run the experiment $$$25 \varepsilon^{-2}$$$ times.
Another approach to estimating how accuracy depends on $$$N$$$ is assuming $$$X$$$ approximates the normal distribution $$$N(\mu,\sigma^2) \approx N(p,\frac{1}{4N})$$$ for big $$$N$$$ (sorry for the ambiguity of the notations), that means $$$2 \sqrt{N}(X-p)$$$ approximates the standard normal distribution $$$N(0,1)$$$. Thus:
So, if we want the probability of getting the wrong answer for a single test to be equal to $$$w$$$, then:
Where $$$\Phi^{-1}$$$ is the quantile function of the standard normal distribution. For example, for $$$w=0.05$$$ $$$N = (0.98 \varepsilon ^{-1}) ^ {2} $$$, for $$$w = 0.01$$$ $$$N = (1.4 \varepsilon ^{-1})^{2}$$$. As you can see, this approach gives a better bound on $$$N$$$ rather than the previous one.
A problem of the kind "Find the area of the given figure with the relative error up to $$$\varepsilon$$$" can be transformed to the problem "Find the probability of a random point thrown in some bounding figure $$$T$$$ belongs to the given figure with the absolute error up to $$$\varepsilon '$$$" with $$$\varepsilon ' \approx \varepsilon$$$.
Submission 59175457 by dorijanlendvaj
Look here:
int MOD=1000000007;
int MOD2=998244353;
Now look here:
void M998()
{
swap(MOD,MOD2);
}
Now look here:

Now look here:

I've answered "YES!", but you should learn that he is wrong; the only evil thing here is the function void M998().
Hello! Codeforces Round 581 (Div. 2) will start on Aug/20/2019 17:35 (Moscow time). The round is rated for everyone whose rating isn't greater than 2099.
The problems were invented and prepared for you by rotavirus, rotavirus and rotavirus. Thanks to Anton arsijo Tsypko for the coordinating the round. Thanks to the testers for testing and giving advice:
You will be given 5 problems and 2 hours to solve them. The score distribution will be announced later is 500-750-1250-(1500+750)-2500.
The round is over! Congratulations to the winners:
1. 79brue
2. sinus_070
3. baluteshih
4. weishenme
5. shahaliali1382
Looking at the "Mo-based solution" of problem 1000F - One Occurrence in editorial, I noticed the author used some sqrt-decomposition to find any element in the set, but the author could do this in O(1) time using the data structure i'll describe right now.
The set which can contain integers from 1 to $$$n$$$ is stored as two arrays of length $$$O(n)$$$:
type set struct {
index []int
val []int
size int
}
func newSet(n int) set {
return set{make([]int,1+n),make([]int,1+n),0}
}
func (s *set) Size() int {
return s.size
}
Inserting into the set:
func (s *set) Insert(x int) error {
n := len(s.index)-1
if x<1 || x>n {
return errors.New("inappropriate value to insert")
}
if s.index[x] != 0 {
return errors.New("value already exists in the set")
}
s.size++
s.val[s.size] = x
s.index[x] = s.size
return nil
}
Erasing from the set:
func (s *set) Erase(x int) error {
n := len(s.index)-1
if x<1 || x>n {
return errors.New("inappropriate value to erase")
}
if s.index[x] == 0 {
return errors.New("value already doesn't exist in the set")
}
i := s.index[x]
if i == s.size {
s.val[s.size] = 0
s.index[x] = 0
s.size--
} else {
y := s.val[s.size]
s.val[s.size] = 0
s.index[y] = i
s.val[i] = y
s.index[x] = 0
s.size--
}
return nil
}
Finding an element in the set:
func (s *set) Find (x int) bool {
n := len(s.index)-1
if x<1 || x>n {
return false
}
return s.index[x]>0
}
Iterating over the set:
func (s *set) ToArray() []int {
return s.val[1:1+s.size]
}
func (s *set) ValueAt(i int) int {
return s.val[i-1]
}
However this set doesn't store values in the ascending order like the standard RB-tree set does.
Sometimes I am asked after solving a problem: what were your approaches? how did you come to the solution? I'll write some blogs about different problems where i'll discuss my thought process.
Problem: 101611F - Fake or Leak?
Submission: submission
1) I know the final results for k teams, and for m - k other teams I may assume anything.
2) For each of k teams in leaked table I should change their results in actual table to their results in leaked table.
3) Now I should sort the teams.
4) If there are any nonleaked teams between the best leaked and the worst leaked team, I should try to upgrade them so they become better than the best leaked team (i can't make them worse than the worst leaked team), else the list of leaked teams can't be consecutive.
5) How should i upgrade the teams in the best way? Assume they solve everything that weren't solved at 240th minute.
6) If I can succesfully upgrade each such team, then the answer is Leaked, else the answer is Fake.
thanks for reading!
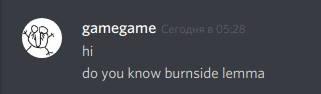
Consider some object that can be represented as a sequence of something with some magic property. Magic property means we consider two such objects equal if one object can be obtained from another using some given permutation. For example, look at these equal necklaces of 8 elements with magic property "we consider two necklaces equal if one can be obtained from another with rotating":
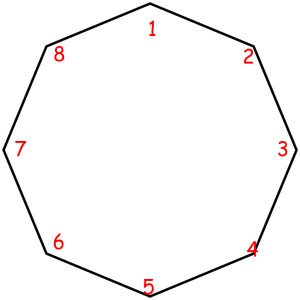
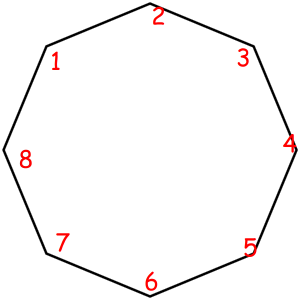
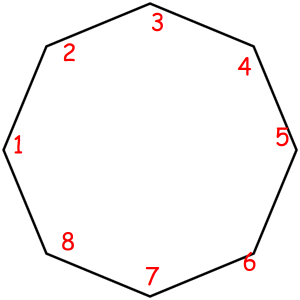
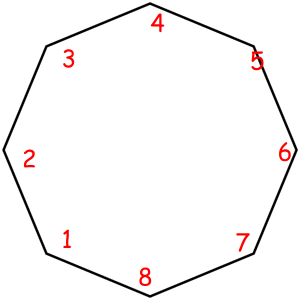
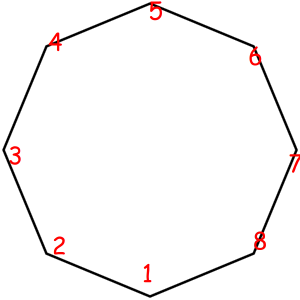
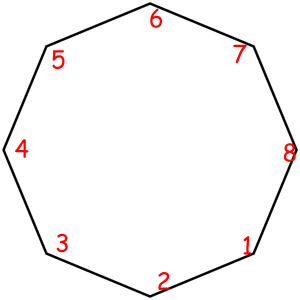
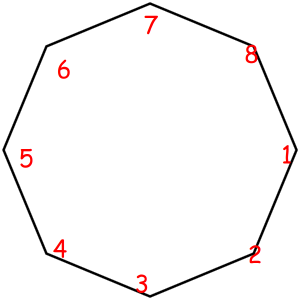
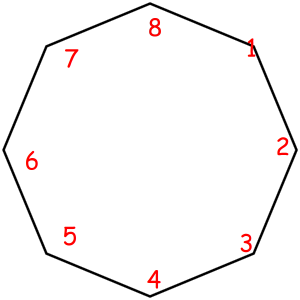
The corresponded special permutations are: 12345678, 23456781, 34567812, 45678123, 56781234, 67812345, 78123456, 81234567
Or look at these equal binary trees of size 7 with a magic property "we consider two trees equal if we can obtain one from another with permuting children of some vertexes":
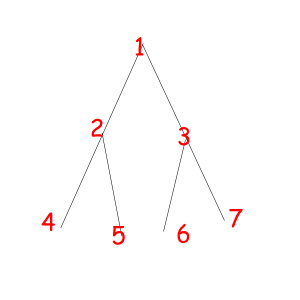

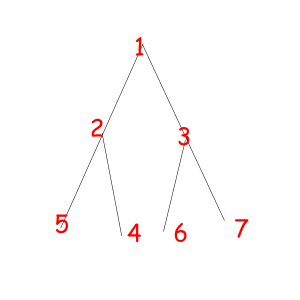
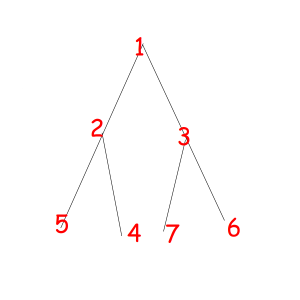
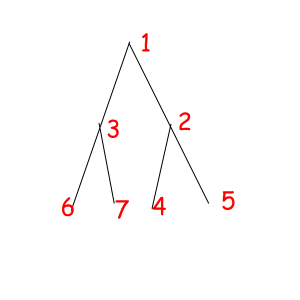
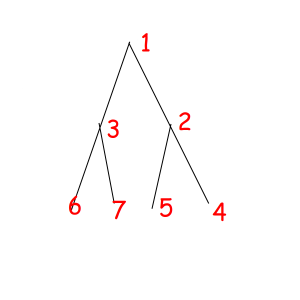
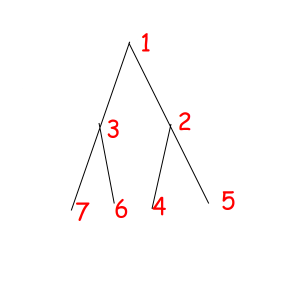
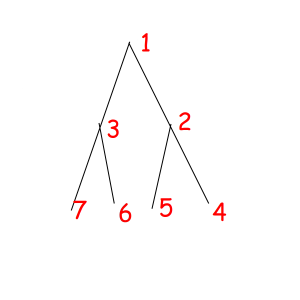
The corresponded special permutations are: 1234567, 1234576, 1235467, 1235476, 1326745, 1326754, 1327645, 1327654.
Now we are given a problem: we have such an object with a magic property, and in how many ways we can paint elements of its sequence in k colours if we count equal paintings as one? According to burnside's lemma for this case, the answer is 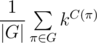 , where G is the set of special permutations, C(π) is the number of cycles in permutation π.
, where G is the set of special permutations, C(π) is the number of cycles in permutation π.
Let's try to solve this problem for reviewed binary tree with 7 vertexes:
G = (1234567, 1234576, 1235467, 1235476, 1326745, 1326754, 1327645, 1327654)
C(1234567) = 7: 1, 2, 3, 4, 5, 6, 7
C(1234576) = 6: 1, 2, 3, 4, 5, 6 - 7
C(1235467) = 6: 1, 2, 3, 4 - 5, 6, 7
C(1235476) = 5: 1, 2, 3, 4 - 5, 6 - 7
C(1326745) = 4: 1, 2 - 3, 4 - 6, 5 - 7
C(1326754) = 3: 1, 2 - 3, 4 - 6 - 5 - 7
C(1327645) = 3: 1, 2 - 3, 4 - 7 - 5 - 6
C(1327654) = 4: 1, 2 - 3, 4 - 7, 5 - 6
So the answer is 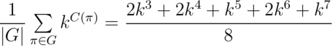
Consider two persons: me, who was able to easily solve div2 A and B when I had just started cp (my only preparations were math background and knowledge of languages) and noname grey/green coder who have participated in 10-20 contests but sometimes still stucks at div2 A. For me, it means the talent exists and is rather important in sports programming.
Can hard work and learning help to reach expert/cm? Is there an universal method to improve yourself? I think no. If yes, then 90% cf users could solve div2 ABC, but it is not true. The hard work and learning is required to get better when you can at least solve div2 AB; div2 A requires only some thinking and div2 B requires only some basics, but without a talent it is useless to try, it is better to do something else.
Downvote if you sure any person can be grandmaster.
Recently, There seems to be so many respected fake accounts.
We should not respect them. If we respect all accounts, then we respect some person twice (by respecting his main and alt accounts). It is unfair for those who doesn't have fake accounts, because they gain our respect only once. So we should stop respect them.
Seems like there are 4 pages of unjudged submissions ...
How to use FFT with 998244353?
Hi, Codeforces!
If two or three problems in div1 round have near the same difficulty and the next problem is much more difficult than that 2 or 3, than results are unfair: participants that solved these problems are sorted according to luck, not to their real skill. Examples:
Also hacking is near impossible in div1 rounds because participants are rather clever to make mistakes.
So I think that div1 rounds should be extended with div2 problems or div1 participants should compete with div2 contestants,
What is your opinion on this ideas?
| Name |
|---|


