I thought of this problem while discussing 343C - Read Time with my friend. It's basically the same idea as 343C - Read Time but over two dimensions instead of one, so I suggest you read the original problem and its solution first.
Spoiler Alert: I briefly talk about the solution to the original problem so don't continue reading if you want to try to solve it for yourself.
Also, it is very possible that the new version of the problem I came up with has already appeared in some form in a competition before. If you are aware of a such problem, Please Link It! Or if you can think of a good solution feel free to share as well! One of the main reasons I'm posting here is because I myself am having trouble coming up with a good solution to this "new" problem.
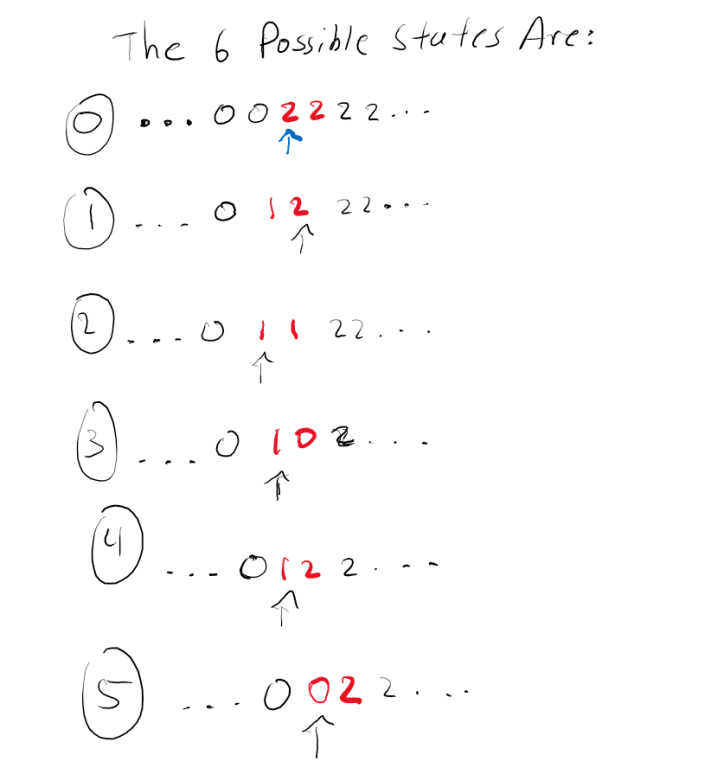
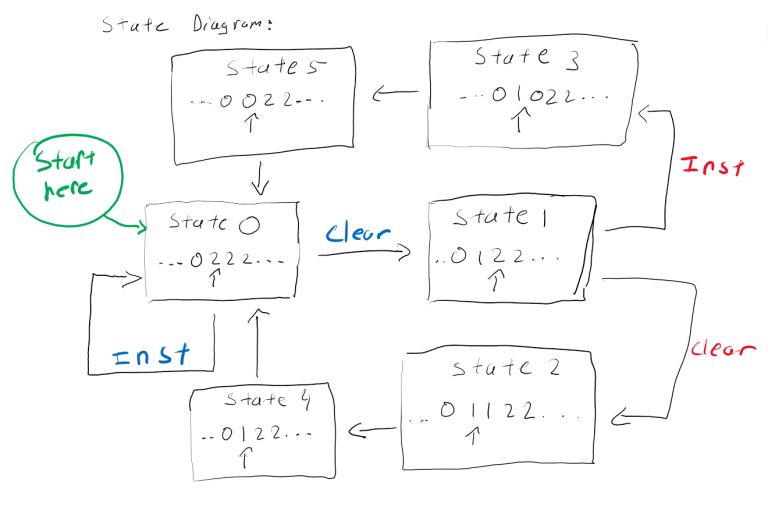
Brief description of the original problem So in the original problem, you essentially have n hard drive heads that can move left and right and m hard drive tracks that must be read located along a 1-dimensional number line. Each head can move left/right by 1 track in 1 second of time, and you are trying to find the minimum time it takes to read all the tracks that you want to read.
The solution is to first sort all n heads and tracks that you want to read, and then you can simply do a binary search for the minimum time because we can check if it is possible to read all the tracks in time t by greedily reading as many tracks as possible starting from the leftmost head.
New version of the problem So the problem I thought of is basically just the same problem but in two dimensions.
Suppose there are n helicopters located throughout an x*y rectangular grid. There are also m bomb sites in the grid where we want to drop a bomb. Assume that each helicopter carries infinite bombs, and it requires no time for a helicopter to drop a bomb. However, the helicopter requires 1 second to move 1 unit length in the grid. Also, the helicopters can move freely, they don't have to move along the gridlines (eg. they can fly diagonally). Find the minimum time it takes for all the helicopters to destroy all the bomb sites. For sake of simplicity, lets assume that all the helicopters and bomb sites are located in integer coordinates.
My thoughts/attempts of a solution So clearly this problem is a lot more complicated than the original problem since now we have to deal with 2 dimensions. My first thought was to use binary search again, but this causes some problems. Suppose that we want to check if the bombsites can be destroyed in less than t seconds. Then we can draw circles of radius t around each helicopter, and then see if the bomb sites lie within the circles. But what if multiple bomb sites occur within one circle? Or what if there are areas where 2 or more circles overlap and the overlapping space has multiple bomb sites in it? So I'm not sure what to do from there.
Please let me know if you have seen this problem somewhere before, or if you have any ideas on how to solve it!