There is hardly any need for improving the time complexity of initializing a Binary Indexed Tree (BIT). Anyway I want to share this neat little trick to initialize a BIT in O(N) time.
Let bit[N] be BIT array and a[N] be the array we need to initialize our BIT with. Notice that for all i we need to add a[i] to positions i, i + (i & -i) and so on in the bit array. Also, a[i + (i & -i)] will also be added to all these positions except i. We can add these 2 in the required places together! Take a look at the following code:
int bit[N], a[N];
void initialize(int n)
{
for(int i=1; i<=n; i++)
{
bit[i] += a[i];
if(i + (i & -i) <= n)
bit[i + (i & -i)] += bit[i];
}
}
Really easy and elegant! Although I have not come across any problems that needed this trick, but there might be a situation where N is too large to initialize the array in O(NlogN) while the number of queries are such that O(logN) per query is feasible (maybe in a 2D BIT problem).
The same technique can be for bulk updates (put update value for position i at a[i] for all N) and even for bulk queries. By bulk I mean number of updates/queries are O(N). Leaving bulk queries as an exercise for the reader :P (its really easy if you understood the above).









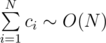 .
.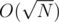 unique costs. So we convert our problem to a bounded knapsack problem with
unique costs. So we convert our problem to a bounded knapsack problem with 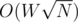 !!!
!!!
