In the contest yesterday Codeforces Round 698 (Div. 1) I submitted 1477B - Nezzar and Binary String two times (105735241 and 105747088), both of the got verdict "TLE on pretest 2". So I spent much time trying to find the reason but failed. Today I just submitted the exactly same code as 105747088, and its verdict changed to "WA on test 2"! (105792669)
The truth is the code was wrong, so WA is the correct verdict. But where did TLE come from?
Could anyone explain about it to me? Thanks a lot!









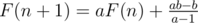
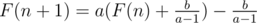
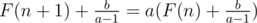
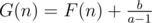 we have
we have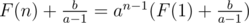
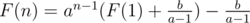
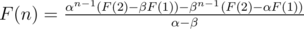
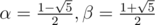
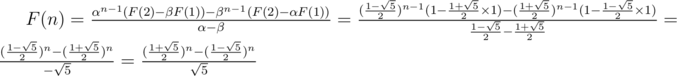
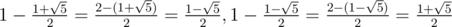 )
)