When I'm looking at Status page an press F5 for big amount of times, sometimes I see such a page: 
No colors, no nice font at "Verdict" column
My reaction:



I look at it and I have oggression and teeth creak
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3880 |
| 2 | jiangly | 3669 |
| 3 | ecnerwala | 3654 |
| 4 | Benq | 3627 |
| 5 | orzdevinwang | 3612 |
| 6 | Geothermal | 3569 |
| 6 | cnnfls_csy | 3569 |
| 8 | jqdai0815 | 3532 |
| 9 | Radewoosh | 3522 |
| 10 | gyh20 | 3447 |
| # | User | Contrib. |
|---|---|---|
| 1 | awoo | 161 |
| 1 | maomao90 | 161 |
| 3 | adamant | 156 |
| 4 | maroonrk | 153 |
| 5 | -is-this-fft- | 148 |
| 5 | atcoder_official | 148 |
| 5 | SecondThread | 148 |
| 8 | Petr | 147 |
| 9 | nor | 144 |
| 10 | TheScrasse | 142 |
When I'm looking at Status page an press F5 for big amount of times, sometimes I see such a page: 
No colors, no nice font at "Verdict" column
My reaction:



I look at it and I have oggression and teeth creak
I was upsolving problem 573C - Bear and Drawing.
My solution 12772765 got wa12.
But after I shuffled nodes it got AC.
Difference is only in line random_shuffle(q.begin(), q.end());
After that I fixed a bug, and solved it honestly 12773232. But imho tests are a little bit weak.
At this problem you need to model what written in statements. Also, it can be proved, that answer can be calculated using formula: 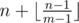 , where ⌊ x⌋ is the integer part of x.
, where ⌊ x⌋ is the integer part of x.
460B - Little Dima and Equation
Obviously S(x) can take only integer values and 1 ≤ S(x) ≤ 81. Let's check S(x) from 1 to 81, and calculate B * S(x)A + C. After that if sum of digits of this number is equal to S(x), it is positive and less than 109, than it is a solution.
There could be bug because of using C++ pow() function.
Note,that answer is positive integer not greater than 109 + 105. Using binary search on answer, we will find answer. Really, we can check in O(n) if some height is achievable. We go from left to right. For current flower we calculate how much times it need to be watered to stand not lower than checking value. If cuurent flower need to be watered for h times, we will star h segments in current flower. We would keep array, in which st[i] — number of segments, which starts in i-th flower. Also, we will keep variable, in which we will keep number of segments, which cover current flower. This variable could be updated at O(1). Really, to get new value we just need to subtract st[i - w], and, if we create new segments, to add st[i]
Also, it can be proved that simple greedy algorithm works. At every of m iterations we can find the leftmost flower with the smallest height and water the segment, which begins in it. Primitive realisation works at O(nm), so you need to use data structure, which can add on segment and find minimum at segment. For example, you can use segment tree with lazy updation or sqrt-decomposition. Such solutions works longer, but faster than TL
Prove: Consider any optimal sequence of moves (using which max. answer reachs). Consider initially the leftmost smallest flower, and suppose all segments which covers it.(suppose, there are at least 1 segment, because else answer is initial height of this flower, so we can put a segment to start in this flower, and answer would not change). Suppose that there are no segments, which starts from current flower. Consider the rightests of segments.(If there are more than one, than any of them). Than, we can move this segment to start in the initially leftmost smallest flower, and the answer would not change. Really, flowers, which earlier was at this segments were higher, than leftmost smallest, and were watered not least times. So, after we moved the answer had not decreased. So, new sequence is also optimal. So, there is sequence of moves, which consists the segment, which starts at the initially leftmost smallest flower. So, let use this. Similary to other of m days, and it would be optimally. 7536171
If r - l ≤ 4 we can all subsets of size not greater than k. Else, if k = 1, obviously that answer is l. If k = 2, answer is 1, because xor of numbers 2x and 2x + 1 equls 1. If k ≥ 4 answer is 0 because xor of to pairs with xor 1 is 0.
If k = 3, we can choose numbers 2x and 2x + 1 with xor 1. So we need to know, if we can get xor equals 0. Suppose that there are 3 such numbers x, y and z (r ≥ x > y > z ≥ l) with xor equals 0. Consider the most non-zero bit of number x. At the same bit of y it's also 1, because xor equls 0, and y > z. Consider the next bit of numbers. If z have 0 there, we have to do next: set the previous bit of numbers x and y equals 0, and set current bit equals 1. Obviously xor still equals 0, z hadn't changed and numbers x and y stood closer to z, so they are still at [l, r].And x > y.Consider the next bit of numbers. If z has zero here than we will change most bits of x и y at the same way and so on. z > 0, so somewhen we will get to bit in which z has 1. Since xor equals 0, the same bit of x would be 1 because x > y, and y would have 0 there. At the next bits we will change bit in x to 0, and in numbers y and z to 1.Finally z would be greater or equal than before, and x would be less or greater than before, and x > y > z would be correct. So, we have the next: if such numbers x, y and z exist than also exist numbers:
1100…000
1011…111
0111…111
with xor equals 0. There are not much such triples, so we can check them.
Formal statement: 2 natural numbers are given: R — radii, and N — number of points. You have to choose N unnesessarily distinct points A1, A2, ...AN which are lying inside or on side of circle, such that
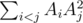
takes its maximal value.
At first let 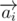 be a vector from (0, 0) to point Ai. Value of
be a vector from (0, 0) to point Ai. Value of 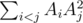 is equal
is equal 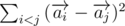 , what is equal to
, what is equal to 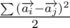 , and it can be rewritten as
, and it can be rewritten as 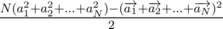 . It makes us think that it is more profitable take point which are close to circle, such that |ai2| would be as big as can, but value of
. It makes us think that it is more profitable take point which are close to circle, such that |ai2| would be as big as can, but value of 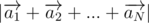 as little as can. After that it becomes obvious, that if N is even, than it's enough to take any diameter and place half of points to the start and another half to the finish of it. Now we're trying to formulate our guessians strictly. Let's take an optimal set of points. Let's mark coordinats as (x1, y1), (x2, y2), ..., (xn, yn).Let's first N - 1 points are fixed, and we can move last point — (x, y). In terms of x, y we'd like to maximize
as little as can. After that it becomes obvious, that if N is even, than it's enough to take any diameter and place half of points to the start and another half to the finish of it. Now we're trying to formulate our guessians strictly. Let's take an optimal set of points. Let's mark coordinats as (x1, y1), (x2, y2), ..., (xn, yn).Let's first N - 1 points are fixed, and we can move last point — (x, y). In terms of x, y we'd like to maximize
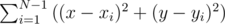
We left out all squares without x, y. Maximization of this x, y function is equivalent to maximization of
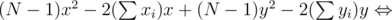
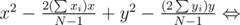
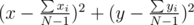
So, we've reduced our problem to finding the furthest integer point from 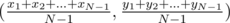 . Now we can declare: the furthest point is placed at one vertex of convex hull of all integer points inside the circle.
. Now we can declare: the furthest point is placed at one vertex of convex hull of all integer points inside the circle.
Proof. Let 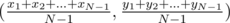 be a point T, and the furthest integer point inside P (convex hull) is X(obviously, it placed somewhere in convex hull). Lets extend TX beyond X to intersection with one side of polygon — let it be AB, and lets mark point of intersection as X'. Clearly TX' ≥ TX. It's easy to see, that one of angles
be a point T, and the furthest integer point inside P (convex hull) is X(obviously, it placed somewhere in convex hull). Lets extend TX beyond X to intersection with one side of polygon — let it be AB, and lets mark point of intersection as X'. Clearly TX' ≥ TX. It's easy to see, that one of angles 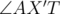 and
and 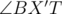 is obtuse, so, according to properties of obtuse triangles on of inequalities holds: TA ≥ TX' ≥ TX or TB ≥ TX' ≥ TX, so, we can replace X to A or B, and distanse TX will increase.
is obtuse, so, according to properties of obtuse triangles on of inequalities holds: TA ≥ TX' ≥ TX or TB ≥ TX' ≥ TX, so, we can replace X to A or B, and distanse TX will increase.
So, we can assume, that every point in optimal set belongs to the convex hull. So, solution is check all sets of points from convex hull and check values on this sets. If R ≤ 30, then convex hull contains no more than 36 points — it's easy to check with computer. So, brute force will take 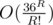 time, and it passes TL easily (depending on realizations and optimizations).
time, and it passes TL easily (depending on realizations and optimizations).
For those, who interested in realization of algorithm: at first we place convex hull to some vector(and points become ordered). After that we build recursion function with the next parameters:1) how many points in the set on this iteration 2) vector with points 3) sum x-coordinats of points from set 4) sum of squares of x- coordinates 5) sum of y-coordinates 6) sum of squares of y-coordinates.
On each iteration we take last point from set, and trying to add all points, starting with this, and finishing on the end of convex hull — it starts new iteration of recursion. Also, we recalculate meaning of cur value in fast way using parameters 3, 4, 5 and 6.
On the last iteration, when we took N points, we are comparing value on this set with maximal value. If maximal value is less, than cur value, then maxvalue = curvalue, and bestvector = cursetofpoints. After recursion we output maxvalue and bestvector.
UPD Editorial of problem C was expanded
| Name |
|---|


