Добрый вечер, друзья!
За обсуждением животрепещущей темы использования чужого кода в своих решениях можно и не заметить, что приближается зима 188 раунд платформы Codeforces!
А ведь мы постарались подготовить для вас набор задач с любопытными (и, как нам хочется думать, не сильно сложными) идеями и понятными условиями.
Мы — это авторы задач yaro и Rei, куратор раундов Codeforces Gerald и автор системы MikeMirzayanov. Отдельное спасибо Паше (PavelKunyavskiy) и Артему (RAD) за тестирование и дельные замечания.
Последний раз, когда я участвовал в проведении соревнования на Codeforces, раунды еще носили статус "beta". Но чем меньше "beta", тем больше ответственность. В связи с этим желаю организаторам и авторам еще одного успешно проведенного раунда. Участникам же — нестандартных задач и идей, чистого кода (а также чистой клавиатуры) и побольше правильно сданных решений!
Нам представляется непростой задачей оценить уровень сложности задач для всей массы участников, поэтому разбалловка будет динамическая. Все же ради любопытства сделаем следующее предположение об относительной сложности задач: div.1: B-B-C-C-E, div.2: A-B-C-C-E. Угадаем ли?
UPD Приносим извинения за проблемы с очередью тестирования Codeforces.
В любом случае, нам будет очень приятно, если вы оцените наш раунд (после его завершения): short survey.
В упорной борьбе с отрывом в один взлом победителем div.1 стал meret (Jakub Pachocki)!
Доступны результаты первого дивизиона, результаты второго дивизиона.









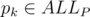 , такой что
, такой что 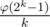 (так как они соответствуют коэффициентам неприводимых множителей круговых многочленов над
(так как они соответствуют коэффициентам неприводимых множителей круговых многочленов над 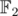 ). Поэтому можно просто брать произвольный набор и проверять его, достаточно скоро мы получим подходящий.
). Поэтому можно просто брать произвольный набор и проверять его, достаточно скоро мы получим подходящий.
