Consider a set of points $$$A$$$, initially it is empty. There are three types of queries:
- Insert a point $$$(x_i, y_i)$$$ to $$$A$$$. It is guaranteed that this point does not belong to $$$A$$$ at this moment.
- Remove a point $$$(x_i, y_i)$$$ from $$$A$$$. It is guaranteed that this point belongs to $$$A$$$ at this moment.
- Given a point $$$(x_i, y_i)$$$, calculate the minimum number of points required to add to $$$A$$$ to make $$$A$$$ symmetrical with respect to the line containing points $$$(0, 0)$$$ and $$$(x_i, y_i)$$$. Note that these points are not actually added to $$$A$$$, i.e. these queries are independent from each other.
The first line contains a single integer $$$q$$$ ($$$1 \le q \le 2 \cdot 10^5$$$) — the number of queries.
Each of the following $$$q$$$ lines describes a query and contains three integers $$$t_i$$$, $$$x_i$$$ and $$$y_i$$$ ($$$ t_i \in \{1, 2, 3\}$$$, $$$1 \le x_i, y_i \le 112\,904$$$) — the type of the query and the coordinates of the point. Type $$$1$$$ is addition of the point, type $$$2$$$ is removal of the point, type $$$3$$$ is the query to compute the minimum number of points required to make $$$A$$$ symmetrical.
It is guaranteed that there are no more than $$$10^5$$$ queries of type $$$3$$$ and no more than $$$10^5$$$ queries having type $$$1$$$ or $$$2$$$.
For each query of the third type output a line with a single integer — the answer to this query.
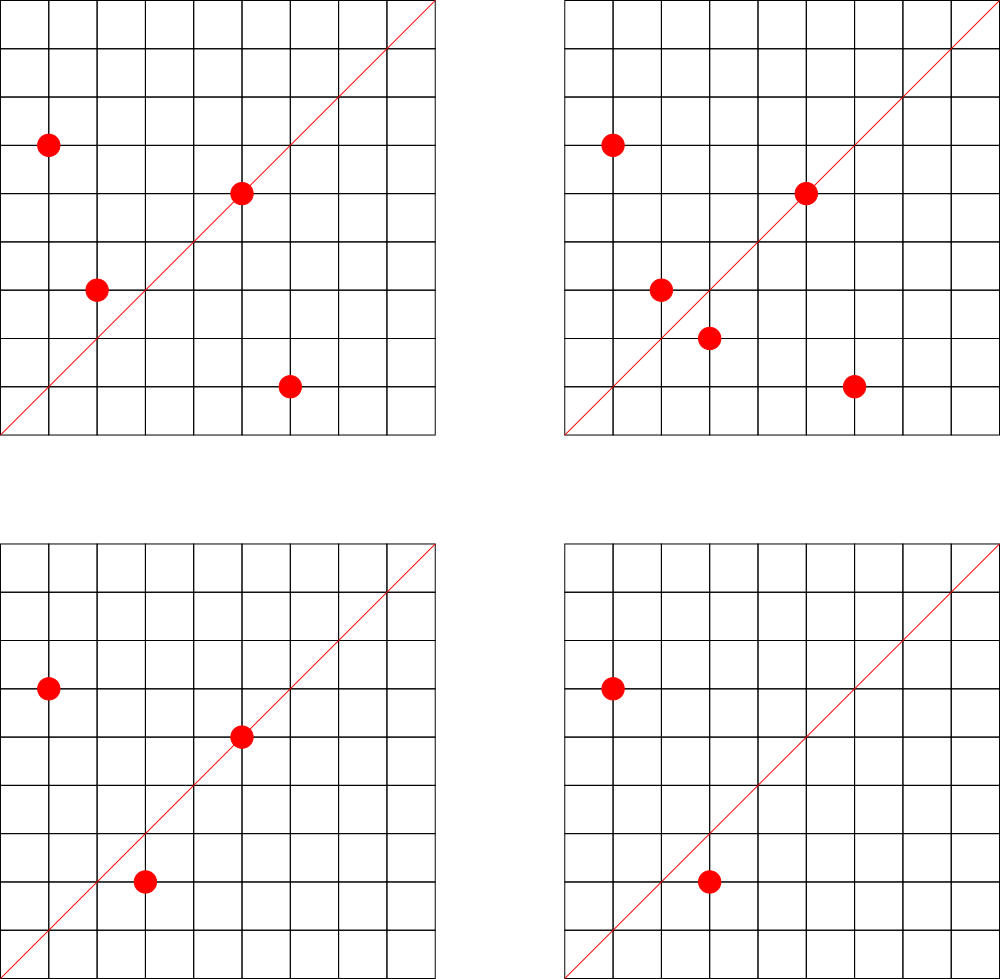
12
1 1 6
1 6 1
1 5 5
1 2 3
3 4 4
1 3 2
3 7 7
2 2 3
2 6 1
3 8 8
2 5 5
3 1 1
1
0
2
2
6
1 1 2
3 1 1
1 1 1
3 2 2
2 1 1
3 2 4
1
1
0
The first example is shown on the picture below.
| Name |
|---|




