| Codeforces Round 564 (Div. 1) |
|---|
| Finished |
Nauuo is a girl who loves playing games related to portals.
One day she was playing a game as follows.
In an $$$n\times n$$$ grid, the rows are numbered from $$$1$$$ to $$$n$$$ from top to bottom, the columns are numbered from $$$1$$$ to $$$n$$$ from left to right. We denote a cell on the intersection of the $$$r$$$-th row and $$$c$$$-th column as $$$(r,c)$$$.
A portal is a pair of doors. You can travel from one of them to another without changing your direction. More formally, if you walk into a cell with a door, you will teleport to the cell with the other door of the same portal and then walk into the next cell facing the original direction. There can not be more than one doors in a single cell.
The "next cell" is the nearest cell in the direction you are facing. For example, if you are facing bottom, the next cell of $$$(2,5)$$$ is $$$(3,5)$$$.
If you walk into a cell without a door, you must walk into the next cell after that without changing the direction. If the next cell does not exist, you must exit the grid.
You have to set some (possibly zero) portals in the grid, so that if you walk into $$$(i,1)$$$ facing right, you will eventually exit the grid from $$$(r_i,n)$$$, if you walk into $$$(1, i)$$$ facing bottom, you will exit the grid from $$$(n,c_i)$$$.
It is guaranteed that both $$$r_{1..n}$$$ and $$$c_{1..n}$$$ are permutations of $$$n$$$ elements. A permutation of $$$n$$$ elements is a sequence of numbers $$$p_1,p_2,\ldots,p_n$$$ in which every integer from $$$1$$$ to $$$n$$$ appears exactly once.
She got confused while playing the game, can you help her to find a solution?
The first line contains a single integer $$$n$$$ ($$$1\le n\le 1000$$$) — the side length of the grid.
The second line contains $$$n$$$ integers $$$r_1,r_2,\ldots,r_n$$$ ($$$1\le r_i\le n$$$) — if you walk into $$$(i,1)$$$ facing right, you should exit the grid from $$$(r_i,n)$$$. It is guaranteed that $$$r_{1..n}$$$ is a permutation of $$$n$$$ elements.
The third line contains $$$n$$$ integers $$$c_1,c_2,\ldots,c_n$$$ ($$$1\le c_i\le n$$$) — if you walk into $$$(1,i)$$$ facing bottom, you should exit the grid from $$$(n,c_i)$$$. It is guaranteed that $$$c_{1..n}$$$ is a permutation of $$$n$$$ elements.
If it is impossible to satisfy the rule, print the only number $$$-1$$$.
Otherwise the first line should contain a single integer $$$m$$$ ($$$0\le m\le\frac{n^2}2$$$) — the number of portals you set.
In the following $$$m$$$ lines, each line should contain four integers $$$x_1,y_1,x_2,y_2$$$, represents that you set a portal consisting of two doors in $$$(x_1,y_1)$$$ and $$$(x_2,y_2)$$$.
If there are multiple answers, print any. You do not have to minimize $$$m$$$.
3 1 3 2 3 1 2
2 1 1 1 3 2 2 3 1
5 3 1 5 4 2 4 2 1 3 5
3 1 1 3 4 2 2 3 2 2 3 5 1
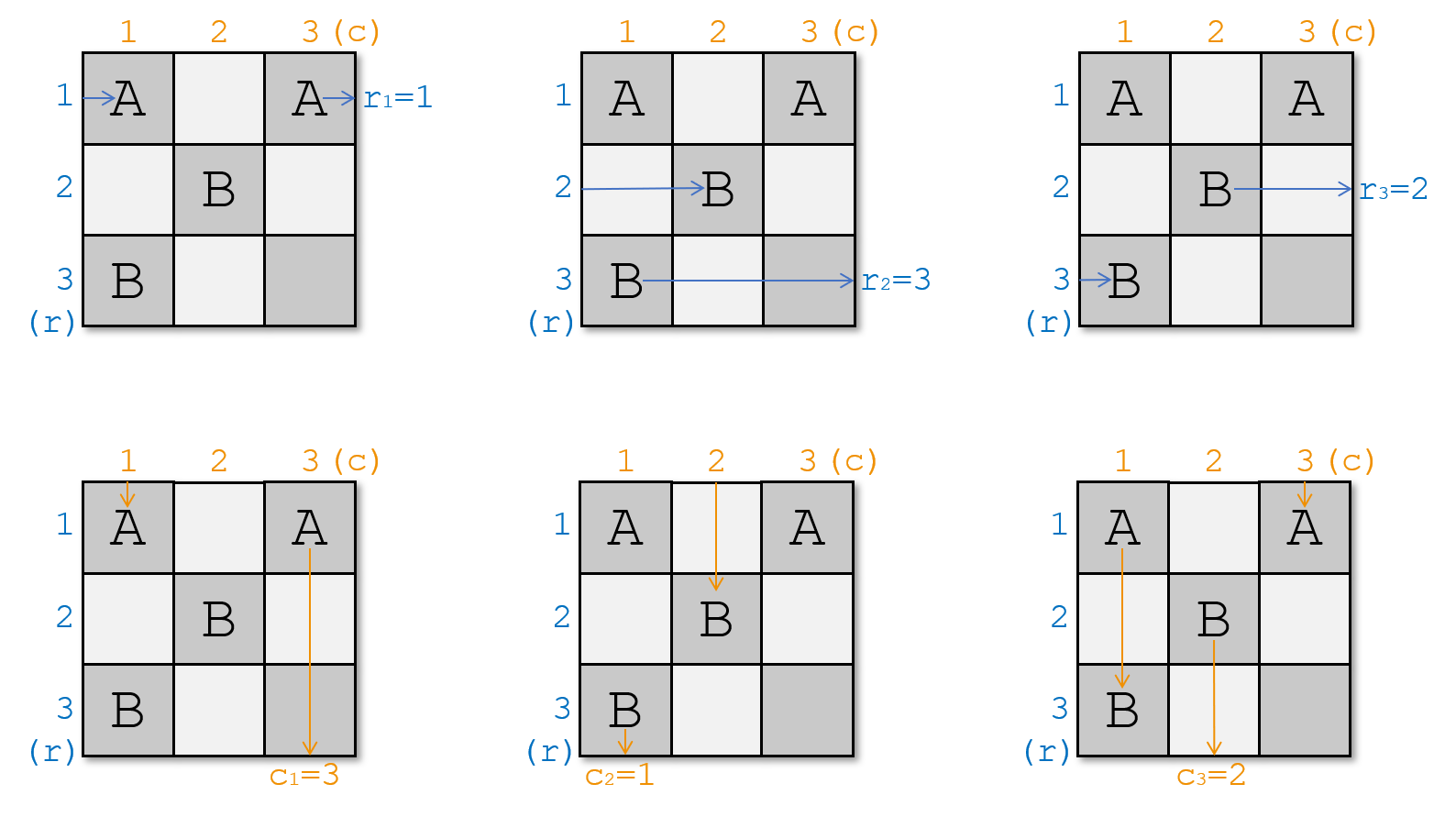
Example 1
The cells with the same letter are a portal. You can set portals in this way:

It satisfies the rule, because:
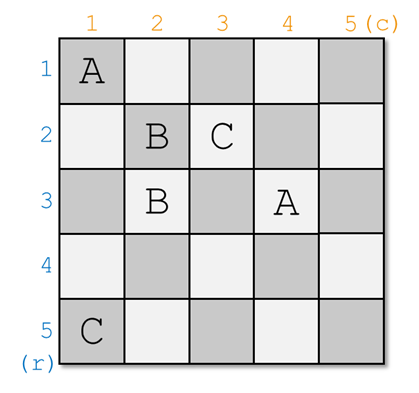
Example 2
You can set portals in this way:
| Name |
|---|




