Idea: ouuan
Consider the two edge cases: all the $$$z$$$ persons upvote / all the $$$z$$$ persons downvote. If the results are the same in these two cases, it is the answer. Otherwise, the result is uncertain.
#include <iostream>
using namespace std;
const char result[4] = {'+', '-', '0', '?'};
int solve(int x, int y)
{
return x == y ? 2 : x < y;
}
int main()
{
int x, y, z;
cin >> x >> y >> z;
cout << result[solve(x + z, y) == solve(x, y + z) ? solve(x, y) : 3];
return 0;
}
Idea: Sulfox
- $$$m\ge\left\lfloor\frac n 2\right\rfloor+1$$$
Consider the chess pieces $$$1$$$ and $$$n$$$.
$$$\because\begin{cases}|r_1-r_n|+|c_1-c_n|\ge n-1\\|r_1-r_n|\le m-1\\|c_1-c_n|\le m-1\end{cases}$$$
$$$\therefore m-1+m-1\ge n-1$$$
$$$\therefore m\ge\frac{n+1}2$$$
$$$\because m\text{ is an integer}$$$
$$$\therefore m\ge\left\lfloor\frac n 2\right\rfloor+1$$$
- $$$m$$$ can be $$$\left\lfloor\frac n 2\right\rfloor+1$$$
If we put the $$$i$$$-th piece on $$$(r_i,c_i)$$$ satisfying $$$r_i+c_i=i+1$$$, it is a feasible plan, because $$$|r_i-r_j|+|c_i-c_j|\ge|r_i+c_i-r_j-c_j|$$$.
#include <cstdio>
using namespace std;
int main()
{
int n, i, ans;
scanf("%d", &n);
ans = n / 2 + 1;
printf("%d", ans);
for (i = 1; i <= ans; ++i) printf("\n%d 1", i);
for (i = 2; i <= n - ans + 1; ++i) printf("\n%d %d", ans, i);
return 0;
}
Idea: QAQAutoMaton
First, try to finish it without playing any empty cards.
If that's not possible, the best choice is to play several empty cards in a row, then play from $$$1$$$ to $$$n$$$. For a card $$$i$$$, suppose that it is in the $$$p_i$$$-th position in the pile ($$$p_i=0$$$ if it is in the hand), you have to play at least $$$p_i - i + 1$$$ empty cards. So the answer will be $$$\max\{p_i-i+1+n\}$$$.
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 200010;
int n, a[N], b[N], p[N], ans;
int main()
{
int i, j;
scanf("%d", &n);
for (i = 1; i <= n; ++i)
{
scanf("%d", a + i);
p[a[i]] = 0;
}
for (i = 1; i <= n; ++i)
{
scanf("%d", b + i);
p[b[i]] = i;
}
if (p[1])
{
for (i = 2; p[i] == p[1] + i - 1; ++i);
if (p[i - 1] == n)
{
for (j = i; j <= n && p[j] <= j - i; ++j);
if (j > n)
{
printf("%d", n - i + 1);
return 0;
}
}
}
for (i = 1; i <= n; ++i) ans = max(ans, p[i] - i + 1 + n);
printf("%d", ans);
return 0;
}
Idea: Sulfox
First, if we choose a node as the root, then each subtree must be in a continuous arc on the circle. Then, we can use DP to solve this problem.
Let $$$f_u$$$ be the number of plans to draw the subtree of $$$u$$$, then $$$f_u=(|son(u)|+[u\ne root])!\prod\limits_{v\in son(u)}f_v$$$ — choose a position for each subtree and then $$$u$$$ itself, then draw the subtrees. However, instead of choosing the position of the root, we suppose the root is on a certain point on the circle, then rotate the circle, thus get the answer: $$$nf_{root}$$$.
In fact, we don't have to write a DP, the answer is $$$n$$$ times the product of the factorial of each node's degree ($$$n\prod\limits_{i = 1}^ndegree[i]!$$$).
#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int N = 200010;
const int mod = 998244353;
int n, ans, d[N];
int main()
{
int i, u, v;
scanf("%d", &n);
ans = n;
for (i = 1; i < n; ++i)
{
scanf("%d%d", &u, &v);
ans = (ll) ans * (++d[u]) % mod * (++d[v]) % mod;
}
cout << ans;
return 0;
}
1172C1 - Nauuo and Pictures (easy version) and 1172C2 - Nauuo and Pictures (hard version)
Idea: ouuan
First, let's focus on a single picture with weight $$$w$$$ which Nauuo likes, so we only have to know the sum of the weights of the pictures Nauuo likes ($$$SA=\sum\limits_{i=1}^nw_i[a_i=1]$$$) and the sum of the disliked ones ($$$SB=\sum\limits_{i=1}^nw_i[a_i=0]$$$) instead of all the $$$n$$$ weights.
Then, we can use DP to solve this problem.
Let $$$f_w[i][j][k]$$$ be the expected weight of a picture Nauuo likes with weight $$$w$$$ after another $$$i$$$ visits since $$$SA=j$$$ and $$$SB=k$$$.
Obviously, $$$f_w[0][j][k]=w$$$.
The state transition:
The next visit displays the picture we focus on. Probaility: $$$\frac w{j+k}$$$. Lead to: $$$f_{w+1}[i-1][j+1][k]$$$.
The next visit displays a picture Nauuo likes but is not the one we focus on. Probaility: $$$\frac{j-w}{j+k}$$$. Lead to: $$$f_w[i-1][j+1][k]$$$.
The next visit displays a picture Nauuo doesn't like. Probaility: $$$\frac k{j+k}$$$. Lead to: $$$f_w[i-1][j][k-1]$$$.
So, $$$f_w[i][j][k]=\frac w{j+k}f_{w+1}[i-1][j+1][k]+\frac{j-w}{j+k}f_w[i-1][j+1][k]+\frac k{j+k}f_w[i-1][j][k-1]$$$.
Let $$$g_w[i][j][k]$$$ be the expected weight of a picture Nauuo doesn't like with weight $$$w$$$ after another $$$i$$$ visits since $$$SA=j$$$ and $$$SB=k$$$. The state transition is similar.
Note that $$$i,\,j,\,k,\,m$$$ have some relation. In fact we can let $$$f'_w[i][j]$$$ be $$$f_w[m-i-j][SA+i][SB-j]$$$ ($$$SA$$$ and $$$SB$$$ are the initial ones here).
But up to now, we can only solve the easy version.
To solve the hard version, let's introduce a lemma:
Proof:
Obviously, this is true when $$$i=0$$$.
Then, suppose we have already proved $$$f_w[i-1][j][k]=wf_1[i-1][j][k]$$$.
$$$\begin{aligned}f_1[i][j][k]&=\frac 1{j+k}f_2[i-1][j+1][k]+\frac{j-1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\\&=\frac2{j+k}f_1[i-1][j+1][k]+\frac{j-1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\\&=\frac{j+1}{j+k}f_1[i-1][j+1][k]+\frac k{j+k}f_1[i-1][j][k-1]\end{aligned}$$$
$$$\begin{aligned}f_w[i][j][k]&=\frac w{j+k}f_{w+1}[i-1][j+1][k]+\frac{j-w}{j+k}f_w[i-1][j+1][k]+\frac k{j+k}f_w[i-1][j][k-1]\\&=\frac{w(w+1)}{j+k}f_1[i-1][j+1][k]+\frac{w(j-w)}{j+k}f_1[i-1][j+1][k]+\frac {wk}{j+k}f_1[i-1][j][k-1]\\&=\frac{w(j+1)}{j+k}f_1[i-1][j+1][k]+\frac {wk}{j+k}f_1[i-1][j][k-1]\\&=wf_1[i][j][k]\end{aligned}$$$
Also, a brief but not so strict proof: the increment in each step is proportional to the expectation.
So, we only have to calculate $$$f_1[i][j][k]$$$ ($$$f'_1[i][j]$$$).
In conclusion:
$$$f'_1[i][j]=1\ (i+j=m)$$$
$$$f'_1[i][j]=\frac{SA+i+1}{SA+SB+i-j}f'_1[i+1][j]+\frac{SB-j}{SA+SB+i-j}f'_1[i][j+1]\ (i+j<m)$$$
$$$g'_1[i][j]=1\ (i+j=m)$$$
$$$g'_1[i][j]=\frac{SA+i}{SA+SB+i-j}g'_1[i+1][j]+\frac{SB-j-1}{SA+SB+i-j}g'_1[i][j+1]\ (i+j<m)$$$
If $$$a_i=1$$$, the expected weight of the $$$i$$$-th picture is $$$w_if'_1[0][0]$$$, otherwise, the expected weight is $$$w_ig'_1[0][0]$$$.
Last question: how to calculate the result modulo $$$998244353$$$?
If you don't know how, please read the wiki to learn it.
You can calculate and store all the $$$\mathcal O(m)$$$ inverses at first, then you can get an $$$\mathcal O(n+m^2+m\log p)$$$ solution instead of $$$\mathcal O(n+m^2\log p)$$$ ($$$p=998244353$$$ here).
#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
const int N = 200010;
const int M = 3010;
const int mod = 998244353;
int qpow(int x, int y) //calculate the modular multiplicative inverse
{
int out = 1;
while (y)
{
if (y & 1) out = (ll) out * x % mod;
x = (ll) x * x % mod;
y >>= 1;
}
return out;
}
int n, m, a[N], w[N], f[M][M], g[M][M], inv[M << 1], sum[3];
int main()
{
int i,j;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; ++i) scanf("%d", a + i);
for (i = 1; i <= n; ++i)
{
scanf("%d", w + i);
sum[a[i]] += w[i];
sum[2] += w[i];
}
for (i = max(0, m - sum[0]); i <= 2 * m; ++i) inv[i] = qpow(sum[2] + i - m, mod - 2);
for (i = m; i >= 0; --i)
{
f[i][m - i] = g[i][m - i] = 1;
for (j = min(m - i - 1, sum[0]); j >= 0; --j)
{
f[i][j] = ((ll) (sum[1] + i + 1) * f[i + 1][j] + (ll) (sum[0] - j) * f[i][j + 1]) % mod * inv[i - j + m] % mod;
g[i][j] = ((ll) (sum[1] + i) * g[i + 1][j] + (ll) (sum[0] - j - 1) * g[i][j + 1]) % mod * inv[i - j + m] % mod;
}
}
for (i = 1; i <= n; ++i) printf("%d\n", int((ll) w[i] * (a[i] ? f[0][0] : g[0][0]) % mod));
return 0;
}
Idea: Sulfox
Consider this problem:
the person in $$$(i,1)$$$ facing right is numbered $$$a_i$$$, the person in $$$(1,i)$$$ facing bottom is numbered $$$b_i$$$. The person numbered $$$p_i$$$ has to exit the grid from $$$(i,n)$$$, the person numbered $$$q_i$$$ has to exit the grid from $$$(n,i)$$$.
The original problem can be easily transferred to this problem. And now let's transfer it into an $$$(n-1)\times (n-1)$$$ subproblem by satisfying the requirement of the first row and the first column.
If $$$a_1=p_1$$$ and $$$b_1=q_1$$$, you can simply do nothing and get an $$$(n-1)\times (n-1)$$$ subproblem.
Otherwise, you can set a portal consisting of two doors in $$$(x,1)$$$ and $$$(1,y)$$$ where $$$a_x=p_1$$$ and $$$b_y=q_1$$$. Swap $$$a_1$$$ and $$$a_x$$$, $$$b_1$$$ and $$$b_y$$$, then you will get an $$$(n-1)\times(n-1)$$$ subproblem.
Then, you can solve the problem until it changes into a $$$1\times1$$$ one.
This problem can be solved in $$$\mathcal O(n)$$$, but the checker needs $$$\mathcal O(n^2)$$$.
#include <iostream>
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
const int N = 1010;
struct Portal
{
int x, y, p, q;
Portal(int _x, int _y, int _p, int _q): x(_x), y(_y), p(_p), q(_q) {}
};
vector<Portal> ans;
int n, a[N], b[N], c[N], d[N], ra[N], rb[N], rc[N], rd[N];
int main()
{
int i;
scanf("%d", &n);
for (i = 1; i <= n; ++i)
{
scanf("%d", b + i);
rb[b[i]] = i;
}
for (i = 1; i <= n; ++i)
{
scanf("%d", a + i);
ra[a[i]] = i;
}
for (i = 1; i <= n; ++i) c[i] = d[i] = rc[i] = rd[i] = i;
for (i = 1; i < n; ++i)
{
if (c[i] == ra[i] && d[i] == rb[i]) continue;
ans.push_back(Portal(i, rc[ra[i]], rd[rb[i]], i));
int t1 = c[i];
int t2 = d[i];
swap(c[i], c[rc[ra[i]]]);
swap(d[i], d[rd[rb[i]]]);
swap(rc[ra[i]], rc[t1]);
swap(rd[rb[i]], rd[t2]);
}
printf("%d\n", ans.size());
for (auto k : ans) printf("%d %d %d %d\n", k.x, k.y, k.p, k.q);
return 0;
}
Idea: ODT
For each color, we can try to maintain the number of simple paths that do not contain such color.
If we can maintain such information, we can easily calculate the number of simple paths that contain a certain color, thus get the answer.
For each color, we delete all nodes that belong to such color, thus splitting the tree into some clusters (here we define a "cluster" as a connected subgraph of the original tree).
By maintaining $$$\sum\text{cluster size}^2$$$, we can get the number of simple paths that do not contain such color.
For each color we try to maintain the same information, add them together, and get the answer.
So now the problem is: a white tree
reverse the color of a node ( white <-> black )
output $$$\sum\text{cluster size}^2$$$
This problem can be solved by many data structures like top tree, link/cut tree or heavy path decomposition.
Let's use the link/cut tree for example.
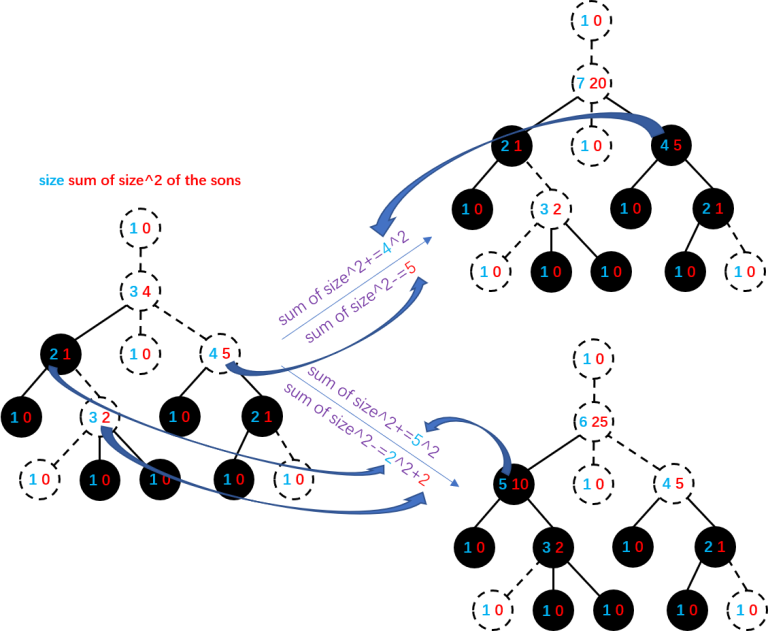
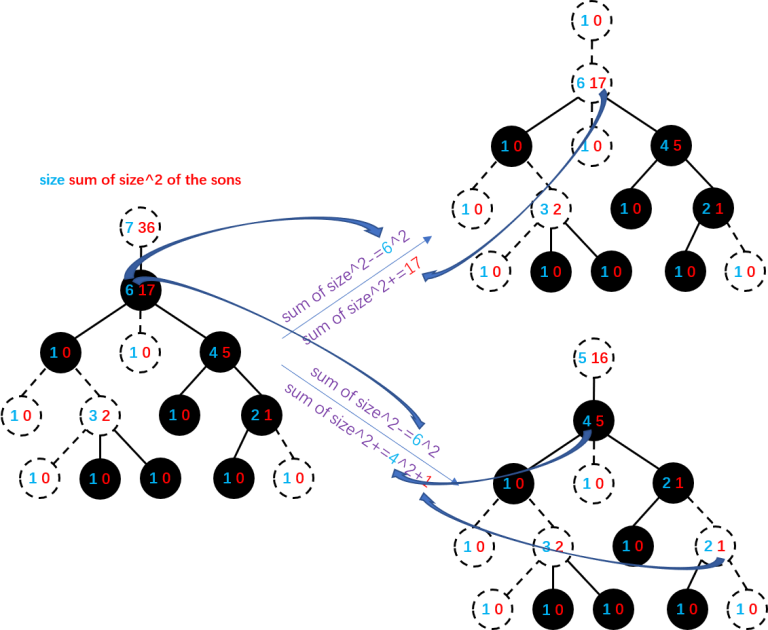
You can maintain the size of each subtree and the sum of $$$\text{size}^2$$$ of each node's sons. Link/cut one node with its father (choose a node as the root and make the tree a rooted-tree first) when its color changes. In this way, the real clusters are the ones that are still connected after deleting the top node of a cluster in the link/cut tree. Update $$$\sum\text{cluster size}^2$$$ while linking/cutting.
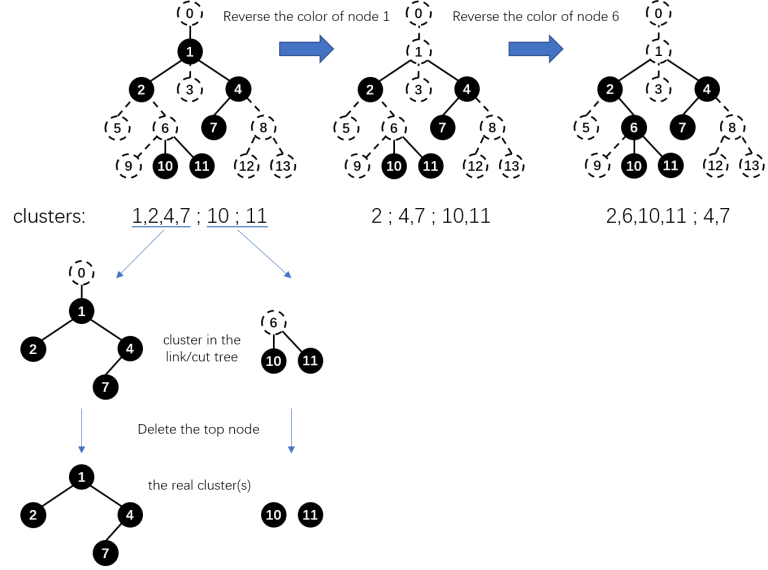
link:
cut:
#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#include <iostream>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 400010;
struct Node
{
int fa, ch[2], siz, sizi;
ll siz2i;
ll siz2() { return (ll) siz * siz; }
} t[N];
bool nroot(int x);
void rotate(int x);
void Splay(int x);
void access(int x);
int findroot(int x);
void link(int x);
void cut(int x);
void pushup(int x);
void add(int u, int v);
void dfs(int u);
int head[N], nxt[N << 1], to[N << 1], cnt;
int n, m, c[N], f[N];
ll ans, delta[N];
bool bw[N];
vector<int> mod[N][2];
int main()
{
int i, j, u, v;
ll last;
scanf("%d%d", &n, &m);
for (i = 1; i <= n; ++i)
{
scanf("%d", c + i);
mod[c[i]][0].push_back(i);
mod[c[i]][1].push_back(0);
}
for (i = 1; i <= n + 1; ++i) t[i].siz = 1;
for (i = 1; i < n; ++i)
{
scanf("%d%d", &u, &v);
add(u, v);
add(v, u);
}
for (i = 1; i <= m; ++i)
{
scanf("%d%d", &u, &v);
mod[c[u]][0].push_back(u);
mod[c[u]][1].push_back(i);
c[u] = v;
mod[v][0].push_back(u);
mod[v][1].push_back(i);
}
f[1] = n + 1;
dfs(1);
for (i = 1; i <= n; ++i) link(i);
for (i = 1; i <= n; ++i)
{
if (!mod[i][0].size())
{
delta[0] += (ll)n * n;
continue;
}
if (mod[i][1][0])
{
delta[0] += (ll)n * n;
last = (ll)n * n;
} else
last = 0;
for (j = 0; j < mod[i][0].size(); ++j)
{
u = mod[i][0][j];
if (bw[u] ^= 1)
cut(u);
else
link(u);
if (j == mod[i][0].size() - 1 || mod[i][1][j + 1] != mod[i][1][j])
{
delta[mod[i][1][j]] += ans - last;
last = ans;
}
}
for (j = mod[i][0].size() - 1; ~j; --j)
{
u = mod[i][0][j];
if (bw[u] ^= 1)
cut(u);
else
link(u);
}
}
ans = (ll) n * n * n;
for (i = 0; i <= m; ++i)
{
ans -= delta[i];
printf("%I64d ", ans);
}
return 0;
}
bool nroot(int x) { return x == t[t[x].fa].ch[0] || x == t[t[x].fa].ch[1]; }
void rotate(int x)
{
int y = t[x].fa;
int z = t[y].fa;
int k = x == t[y].ch[1];
if (nroot(y)) t[z].ch[y == t[z].ch[1]] = x;
t[x].fa = z;
t[y].ch[k] = t[x].ch[k ^ 1];
t[t[x].ch[k ^ 1]].fa = y;
t[x].ch[k ^ 1] = y;
t[y].fa = x;
pushup(y);
pushup(x);
}
void Splay(int x)
{
while (nroot(x))
{
int y = t[x].fa;
int z = t[y].fa;
if (nroot(y)) (x == t[y].ch[1]) ^ (y == t[z].ch[1]) ? rotate(x) : rotate(y);
rotate(x);
}
}
void access(int x)
{
for (int y = 0; x; x = t[y = x].fa)
{
Splay(x);
t[x].sizi += t[t[x].ch[1]].siz;
t[x].sizi -= t[y].siz;
t[x].siz2i += t[t[x].ch[1]].siz2();
t[x].siz2i -= t[y].siz2();
t[x].ch[1] = y;
pushup(x);
}
}
int findroot(int x)
{
access(x);
Splay(x);
while (t[x].ch[0]) x = t[x].ch[0];
Splay(x);
return x;
}
void link(int x)
{
int y = f[x];
Splay(x);
ans -= t[x].siz2i + t[t[x].ch[1]].siz2();
int z = findroot(y);
access(x);
Splay(z);
ans -= t[t[z].ch[1]].siz2();
t[x].fa = y;
Splay(y);
t[y].sizi += t[x].siz;
t[y].siz2i += t[x].siz2();
pushup(y);
access(x);
Splay(z);
ans += t[t[z].ch[1]].siz2();
}
void cut(int x)
{
int y = f[x];
access(x);
ans += t[x].siz2i;
int z = findroot(y);
access(x);
Splay(z);
ans -= t[t[z].ch[1]].siz2();
Splay(x);
t[x].ch[0] = t[t[x].ch[0]].fa = 0;
pushup(x);
Splay(z);
ans += t[t[z].ch[1]].siz2();
}
void pushup(int x)
{
t[x].siz = t[t[x].ch[0]].siz + t[t[x].ch[1]].siz + t[x].sizi + 1;
}
void add(int u, int v)
{
nxt[++cnt] = head[u];
head[u] = cnt;
to[cnt] = v;
}
void dfs(int u)
{
int i, v;
for (i = head[u]; i; i = nxt[i])
{
v = to[i];
if (v != f[u])
{
f[v] = u;
dfs(v);
}
}
}
Idea: rushcheyo
At first, let's solve this problem in $$$\mathcal{O}(n\sqrt{n \log n})$$$.
Let's split our array into blocks by $$$B$$$ integers, and let's find a function, $$$f(x) = $$$ which value you will get at the end of the current block if you will start with $$$x$$$. With simple induction, you can prove that this function is a piece-wise linear, and it has $$$\mathcal{O}(B)$$$ segments, so you can build it iteratively in $$$\mathcal{O}(B^2)$$$ time for each block, so the preprocessing took $$$\mathcal{O}(nB)$$$.
And to answer the query, you can keep the current value of $$$x$$$ and then find with binary search by that piece-wise linear function the $$$f(x)$$$ for the current block.
With a good choice of $$$B$$$, this solution will work in $$$\mathcal{O}(n\sqrt{n \log n})$$$.
Ok, but then how to solve it in $$$\mathcal{O}(n \log + q \log^2)$$$?
Lemma: each segment of this piece-wise linear function has length at least $$$p$$$.
You can prove it with simple induction.
And then, with this lemma, it is possible by two functions $$$f(x)$$$ of size $$$n$$$ and $$$g(x)$$$ of size $$$m$$$ find the new function $$$h(x) = g(f(x))$$$, in the $$$\mathcal{O}(n + m)$$$, you can do it with two pointers, similar to the previous iterative method, but adding a several points to the function each time, best way to understand it is to check the indendent solution :)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1000005;
const ll inf = (ll)1e16;
int n, m, P, a[N];
ll sum[N];
vector<ll> func[N << 2];
vector<ll> merge(int l, int r, int mid, const vector<ll> &f, const vector<ll> &g) {
ll suml = sum[mid] - sum[l - 1], sumr = sum[r] - sum[mid];
vector<ll> ret(f.size() + g.size() - 1, inf);
for (int i = 0, j = 0; i < (int)f.size(); ++i) {
ll xl = f[i], xr = (i + 1 == (int)f.size() ? inf : f[i + 1] - 1), yl = xl + suml - (ll)i * P, yr = xr + suml - (ll)i * P;
while (j > 0 && g[j] > yl) --j;
while (j < (int)g.size() && (j == 0 || g[j] <= yl)) ++j;
--j;
for (; j < (int)g.size() && g[j] <= yr; ++j)
ret[i + j] = min(ret[i + j], max(xl, g[j] - suml + (ll)i * P));
}
ret[0] = -inf;
return ret;
}
void build(int u, int l, int r) {
if (l == r) {
func[u].push_back(-inf);
func[u].push_back(P - a[l]);
return;
}
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
func[u] = merge(l, r, mid, func[u << 1], func[u << 1 | 1]);
}
ll query(int u, int l, int r, int ql, int qr, ll now) {
if (l >= ql && r <= qr)
return now + sum[r] - sum[l - 1] - (ll)P * (upper_bound(func[u].begin(), func[u].end(), now) - func[u].begin() - 1);
int mid = l + r >> 1;
if (qr <= mid)
return query(u << 1, l, mid, ql, qr, now);
if (ql > mid)
return query(u << 1 | 1, mid + 1, r, ql, qr, now);
return query(u << 1 | 1, mid + 1, r, ql, qr, query(u << 1, l, mid, ql, qr, now));
}
int main() {
scanf("%d%d%d", &n, &m, &P);
for (int i = 1; i <= n; ++i)
scanf("%d", a + i), sum[i] = sum[i - 1] + a[i];
build(1, 1, n);
for (int l, r; m--;) {
scanf("%d%d", &l, &r);
printf("%I64d\n", query(1, 1, n, l, r, 0));
}
return 0;
}
We had prepared a problem similar to 1174F - Ehab and the Big Finale before that round, so we needed to prepare new problems in four days. It was in such a hurry that there are some imperfections in our round. Please accept our sincere apology.










someone please help with the proof of div2c/div1a
The approach is that you have to play some blank cards in the beginning and then play the cards 1 to n in a row. So if you see by taking examples. Now suppose you are starting your moves for playing cards 1 to n. So what are the requirement: Card 1 present in hand. Card 2 present in hand or at the top of the pile. Card 3 present in the hand or at the top or the second from top in the pile ... and so on. Suppose some condition is violated, then we have to play blank cards to get the card i before its turn to play comes. That comes out to be pi — i + 1. If we play these many blank cards so the top of pile above this position are already in our hand. So the ans is max(pi — i + 1) + n. We add n for playing the cards 1 to n.
can you please explain how that p_i -i +1 come up? thank you
I thought like this. let element position is p[i] then before it's extraction i can have p[i]-1 element in correct position if it is present in our hand. Now that element position in sequence should be i, so to extract it i-p[i]+1 empty cards should be added. Please tell if I am wrong or u have some different observation
Your approach is totally cool.
I viewed the Div2C from a different perspective, and ended up with the same solution.
Let p_k be the 0-based index of card k. If card k is in our hand, then p_k = -1 . After our t-th move, we will receive the card located at index p_t — 1. Ideally, we would like for p_k + 1 < k, for all k; this means that we would acquire all of the cards "just in time" to play the them in order. In this case, the answer would be n.
However, the p_k + 1 < k condition might not hold for all k. In order to remedy this issue, we can begin by playing a series of 0-cards. Note that playing a 0-card is optimal as a different action would send a non-zero card to the bottom of the deck. In essence, we would be decreasing the value of each p_k by z by playing z 0-cards at the beginning; the 0-cards would essentially be functioning as an offset. This means that we can rewrite our original inequality in the following manner: p_k — z + 1 < k. Via a bit of algebra, we find that p_k + 1 — k < z.
Since we want to minimize the total number of cards played, it would be wise to minimize z. This can be achieved by finding the maximum value of p_k + 1 — k. Thus, our final solution would be n + max{p_k + 2 — k}, for k = 1,...n.
Accepted Solution: https://codeforces.com/contest/1173/submission/55285031
How did
p_k + 1 - kbecomep_k + 2 - kin the last line?I have the same doubt
I guess it is because of the 0 based vs 1 based indexing.
The value of z is constrained to the z > p_k + 1 — k condition. We can relax this condition by adding 1 to the right-hand side: z ≥ p_k + 2 — k.
it needs not that much proof...You can find that the ans will not larger than 2n,since you can just keep all the 1...n in the order from your hand(a[]) in less than n turns...and what you need is just to calc the turns you need when 0<=ans<=n or n<ans<=2n. The samples are good, it covers all the situation. You can find if your push 1 to n into the b[] from T turns,there are some limits to all the numbers.
Can someone please give a less mathematical explanation of divison 2 problem B?
The approach is pretty straight here, the aim is to minimize m given n pieces and if you see the inequality in an easier way, it is as follows: "The next piece should be at least 1 more row or column away from the previous piece, ie r = r + 1 or c = c + 1". So since you need to minimize the number of rows and columns of the chessboard. What you do is increase it alternatively. So if you visualize it is — (n/2) + 1. And the blocks are alternatively increasing the row or column number. Ex. 1-1 then 1-2 then 2-2 then 2-3 then 3-3.... until all pieces are covered. It will always minimize m.
Well, if this number is divisible by 2, then you will not be able to put the numbers in the square with the n / 2 side, because even if you put 1 and n at opposite corners, the condition will not be fulfilled. If the number is odd, then similar reasoning for a square with a side (n — 1) / 2. How to put numbers in a larger square is clear from the code.
Just put them in the pieces in the first row, then the last column. You'll notice that the Manhattan distance of the pieces always remains the same as abs(i-j).
My Solution
Here's my formal proof for a greedy strategy for Div 2B.
Note: The distance formula used in the problem is the Manhattan distance and I will just refer to it as distance for convenience.
Let the cell on which we place our first piece (it must be piece number 1) be $$$S$$$. Let the cell which is farthest from $$$S$$$ be $$$T$$$.
Lemma: Assuming that distance between $$$S$$$ and $$$T$$$ $$$\ge$$$ $$$n$$$, for any choice of such $$$S$$$, we can always find a sequence of cells to place all chess pieces.
Proof: Formally, the distance between $$$S$$$ and $$$T$$$ is $$$R' + C'$$$ where $$$R'$$$ is the distance in rows only and $$$C'$$$ is the distance in columns only. Let's use the following strategy:
We will always place the piece, with the next higher numbering, such that it is in either the same row or same column as the previous piece. Furthermore, this piece shall be placed such that it is closer to $$$T$$$ than the previous piece.
Notice that this strategy will ensure that the distance between $$$T$$$ and the new piece will be $$$R' - i + C'$$$ OR $$$R' + C' - i$$$ where $$$i$$$ is the piece number. Furthermore, this strategy is feasible because the distance between the new piece and the previous piece is exactly $$$1$$$.
We just keep applying this strategy until we have exhausted all our pieces. We will always be able to use all our pieces because $$$R' + C' \ge n$$$ as per our initial assumption. Q.E.D.
Now, this is an optimal strategy because for any solution, the distance between $$$S$$$ and $$$T$$$ $$$\ge$$$ $$$n$$$. But we used exactly $$$n$$$ steps.
To ensure that the assumption in our lemma holds for any feasible board size, we should choose $$$S$$$ to be the upper-left/upper-right/lower-left/lower-right corners of the board. This is because, this maximizes the distance between $$$S$$$ and $$$T$$$.
From here, all we need to do is to find the minimum size of $$$m$$$ such that our assumption still holds. Notice that for our strategy, we require that that $$$2m - 1 >= n $$$ (Draw a diagram to see why). Solve this inequality to get the optimal value of $$$m$$$.
In case you didn't understand my strategy, see my submission.
Cheers. LTDT.
How to see on what pretest(input) the code gives wrong answer ?
thats not visible
Can someone explain to me how can we just take factorial of degree? I mean how are we assuring that there will be no intersections in any of those permutation? Like if node A has edges to X different nodes. Then if I swap any two nodes in X, how will not intersect? I hope my doubt clear.
If you understand the dp solution, you can expand the dp formula, and get $$$n\prod\limits_{i = 1}^ndegree[i]!$$$.
Can you please elaborate the expansion and also the DP equation.
As we are excluding the root shouldn't the factorial of (degree-1) be taken ?
$$$|son(root)|=degree(root)$$$, $$$|son(u\ne root)|=degree(u)-1$$$.
Then how come the answer of test case 1 is 16 and not 8(4 * 2! * 1! * 1!)
the degrees on test case 1 are 2, 2, 1, and 1.
But for non root-node we should consider degree-1.
Shouldn't we ?
You will have "degree" number of choices for the position of "non-root node". For instance, you have node A and its parent B. Firstly, you will have an arc containing A and its subtree on the circle and an edge coming from B to A, separating the arc into two parts. Therefore, you will need to divide A's children into two parts and put A between them. Since you have "degree-1" number of children, you will have (degree-1)! number of permutations times (degree) number of choices for A --> a total of (degree)! number of choices at A.
May someone please explain how m≥[n/2]+1 was derived for Div 2 B? Thank you very much.
for any m you can place at max 2*(m-1)+1 i.e. all elements can be present in 1st column and last row. If you enter more than that number of elements condition will be violated
Can anyone please explain how the if(j > n) condition would ever be fulfilled in the editorial of div2c? Thanks in advance! :)
It means the loop exits not because of
p[j] > j - i, butj > n.Oh, got it. Thanks!
Could someone explain me the problem 1172B — Nauuo and Circle, why if u is root then f[u] = (|son[u]|)! ... and when u is not root then f[u]=(|son[u]|+1)! ... .
Because for the root, the arcs of its subtrees is in a cycle (the head and tail are connected), it's the same no matter where you put the root.
For example: you put the root and each subtree in this way:
2, root, 3, 4, then changed root's place:2, 3, root, 4, but the second one is the same asroot, 4, 2, 3,3, root, 4, 2and4, 2, 3, root.Oh! I got it. Thank you so much :3
div2 C (-_-)
real
Div1C is an extraordinarily nice problem and has a beautiful proof with this lemma. I had a time gradually transforming my solution from [2][M][M][M][N] to [2][M][N] complexity. Kudos for the problem.
Can someone explain the editorial of 1172B - Nauuo and Circle?
I could not get any part of it.
I have tried to explain my solution here.
Could someone please tell the solution of div2c/div1a in a greedy way?I write a greedy one but it is wrong when I test it on my computer during the contest ): So I would like to know where are the bugs.Thanks.
I think greedy way only works when the ans is lower than n.
ouuan
This problem can be solved by many data structures like top tree, link/cut tree or heavy path decomposition.
I am really curious what is it a top tree? Do you mean centroid decomposition?
A top tree is a tree structure of "top clusters". Consider a connected subgraph on tree, if there are only two vertices which have edges with outside, we call the subgraph "top cluster". Top trees have very strong ability but the whole top trees are very hard to implement in the contest. Instead we often use a simplified version called "the subtree maintaining tricks of link/cut tree". You can learn more on https://en.wikipedia.org/wiki/Top_tree.
Please, what kind of data may the 9th point of div1E be? I don't think my code has any difference with the solution, and it can also solve big data in time on my computer, but it is TLE with the 9th point, so I think there may be something special that I haven't thought. > <
Oh it seems like my arrays are too small. Now it's OK.
My solution for Div2C/Div1A Nauuo and Cards The idea is that if you want to place a particular card at the bottom of the pile, you need to have it in your hand beforehand. The other major point to notice is that you'll have to place all the cards upto card n in a sequential manner. If you miss any 1 card from the sequence (cause you don't have it), you'll have to place and pick all the cards again (this time some different placing and picking pattern) until you reach at the same position and now you have the required card in your hand.
Another point to notice is that worst case would be to place all the zeroes in the sequence and pick all the n cards. After at most n operations, you have all the card from 1 to n in your hand, and you need more n operations to place it in a sequential manner.
We'll use the idea of binary search here. If the pile can be arranged in x operations, it can definitely be arranged in more than x operations. We need to find out the min value of x such that we are able to build the pile in x operations.
So this is how we check it for x operations :- If the pile can be built in x operations, x will always be greater than n(except for one corner case that I'll discuss later). So the last n operations would be to put all the cards from 1 to n in the pile. We'll talk about the last n operations. In the 1st operation of the last n operation (overall x-nth operation), we must be able to place the card '1' in the pile. This would be possible if the occurence (index) of card '1' in the array 'b[]' is less than (x-n) ,similarly for card 2, the index in array 'b[]' is less than x-n+1 and so on upto card n. We're just checking whether we have the card in hand or not before placing.
If this can be done using x operations, we'll check for operations lesser than x(using binary search)
I have never heard before that linkcut trees can maintain subtree sizes. Are there resources about cool operations that linkcut trees can perform?
You can read this.
I think you are able to read (Simplified) Chinese.
I think the result of $$$Div1$$$ $$$C2$$$ can be reached without a need for the inductive proof. Let the sum of initial weights be $$$Wbig_i$$$. Notice that the expected weight $$$Wbig_e$$$ of a picture with initial weight $$$Wbig_i$$$ of type $$$a$$$, is equal to the expected sum of weights of $$$c$$$ pictures (let this set of pictures be $$$s$$$) of type $$$a$$$, whose initial weights sum up to $$$Wbig_i$$$; This is because the calculation of the expected sum of weights ignores the individual values of weights and just considers the sum of weights (and you add/subtract 1 when visiting some picture, regardless of its initial weight).
And as the expected some of weights is equal to the sum of expected weights (basic probability), therefore $$$Wbig_e$$$ is equal to the sum of the expected weights of $$$s$$$. If all the pictures in $$$s$$$ have the same initial weights, then the expected weight of each of them is $$$Wbig_e/c$$$ (Because 2 pictures with the same initial weights obviously have the same expected weights).
Then we finally can get the expected weight $$$Wsmall_e$$$ of a picture of type $$$a$$$ with initial weight $$$Wsmall_i$$$, by finding a positive integer $$$d$$$ which divides both $$$Wbig_i$$$ and $$$Wsmall_i$$$, then $$$Wsmall_e$$$ will be $$$\frac{Wbig_e}{Wbig_i/d}\cdot\frac{Wsmall_i}{d}$$$, and we can always choose d to be 1.
Yes, I know it's no need to prove it inductively. But I think the inductive proof is easier to write, and is also easier to understand for those who are not so good at probabilities.
The alternative proof for the main lemma in 1173E2 - Nauuo and Pictures (hard version). Let's focus on a case where she likes all the pictures.
There are $$$n$$$ trees, the $$$i$$$-th of them has $$$w_i$$$ vertices. $$$m$$$ times you add a new leaf and attach it to a random vertex. A new vertex is either attached to one of the initially-existing vertices (then the p-bility is $$$w_i / \sum w_i$$$) or it is attached to one of already added vertices. This gives us a trivial proof by induction: if p-bility of adding a vertex to the $$$i$$$-th tree in previous steps is $$$w_i / \sum w_i$$$, then it's the same in this step when we attach the new vertex to one of vertices added in previous steps. So p-bility is $$$w_i / \sum w_i$$$ in every step.
ouuan In problem Div.1 C, why doesn't this approach work? Consider you have the expected weights $$$e_i$$$ of each picture upto $$$m-1$$$ visits. With initial conditions, for $$$m = 0$$$, we have $$$e_i$$$ = $$$w_i$$$. We can update Expected values in the next visit by:
For picture Nauo likes, $$$e_i = e_i + \frac{e_i}{\sum_{j=1}^n e_j}$$$ [previous E.V $$$+$$$ 1 * probability of getting this picture]
For picture Nauo dislikes, $$$e_i = e_i - \frac{e_i}{\sum_{j=1}^n e_j}$$$ [previous E.V $$$-$$$ 1 * probability of getting this picture]
We'll do this for $$$m$$$ times to get final $$$e_i$$$
Because the sum of weights is not fixed when the number of operations is fixed.
Why can't we use expected weights upto $$$m-1$$$ operations as actual weights to compute weights of $$$m^{th}$$$ operation? The expected values are just average weights after $$$m-1$$$ ops, right?
I tried the same thing as S.Jindal, and I wasn't sure why it was incorrect. Each time through the loop I recalculated the sum of the weights using the expected values.
"Because the sum of weights is not fixed when the number of operations is fixed." doesn't mean I thought you didn't recalculate the sum of the weights using the expected values. This sentence is the reason why you can't use the sum of expected values to calculate. You can calculate the example test 3 by hand to see why it is wrong.
What if in Div 1 B the question was about a graph, not necessarily a tree
Can anyone explain div1 B ? Thank you
I have tried to explain my solution here. Hope it helps.
Thank you very much
Problem F in $$$O((n+q)log(q))$$$. This is a bit of a necropost but I think the solutoin is interesting and I don't see any comments about it.
Let's analyze the piecewise function mentioned in the editorial, but only on the values [0; p — 1]. It will be 2 line segments with slope 1 and the image will be some segment [L; L + p — 1].
So f(x) will have the form of f(x) = L + (x + S — L) % p. Or the smallest integer >= p with correct remainder.
Here x % p denotes remainder in range [0; p — 1];
Turns out it's easy to incrementally update the functions parameters L and S if you think about it:
S is just range sum.
So to solve the problem we can go in increasing order of right endpoint and maintain a treap of L values for all queries. The BST needs to support
val+=xandval=0.