I've recently solved this problem and have seen many people asking for an explanation. Well, here is what I did, I hope it helps someone.
The problem can be found here.
Consider the first example.
4
1 2
1 3
2 4
16
That is, we have this:
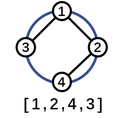 (I just realized I can't upload pics from local PC. Okay ._.)
(I just realized I can't upload pics from local PC. Okay ._.)
Let's assume 1 to be the root node of this tree. So, what we want are different permutations of this. Now pick up 2. What can we do just in this sub tree? (That is, 2 and 4).
We can either have 4 on the left of 2, or in the right of 2. Nothing else is doable here.
What about 3? Well, it doesn't have any children so we can't do much here. So, nothing.
Now let's look at 1. What things are possible?
A lot of things eventually. If we go in a similar way as we did with 2 (that is, all children are taken to one side)
a. You can have 2 and 3 on the left of 1
b. 2 on the left 1 in the middle and 3 on the right
c. 2 and 3 on the right of 1
And 3 more, if we change the ordering of 2 and 3 for each a,b and c.
So basically 6 options.
This looks like we're just creating all the arrangements for the children of a node. Isn't that simply equal to $$$children!$$$ (factorial, not what a pedo would have screamed to his genie).
Well then the answer for 2 should have been $$$1!=1$$$ and not 2. So, we also have to count empty spaces for nodes.
So, we get an idea of $$$(children+1)!$$$. Remember we're not looking at the whole thing until now, node and it's children.
So for 1, we have 2 children, thus $$$(2+1)! = 3! = 6$$$ ways. Well yes, but actually no.
The point where we're taking all children to one side, is wrong actually.
Looking at some bad sketches:
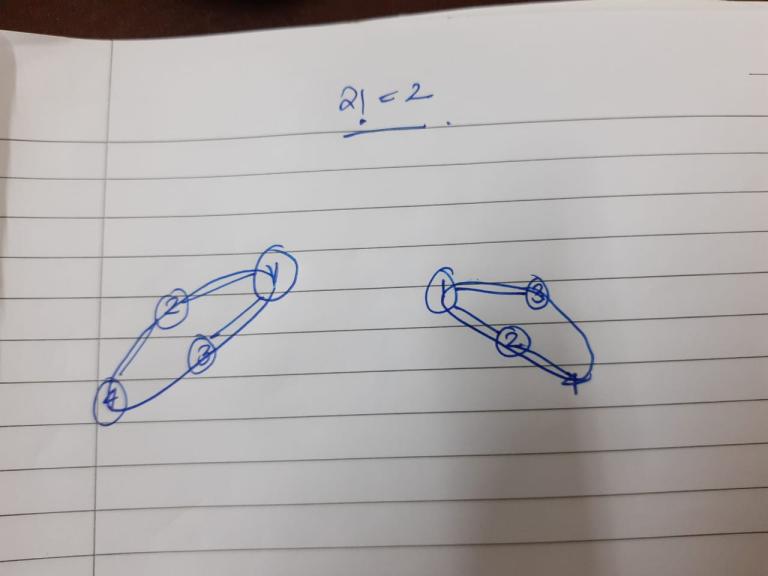
Aren't they both representing the same structure? Yes. So, we remove ways 1 and 3 (and their 2 copies). So we get only two options for node 1:
- 2 on the left of 1, and 3 on the right
- 3 on the left of 1, and 3 on the right
So actually we're using $$$children!$$$ here. So, was our $$$(children + 1)!$$$ wrong? Well actually no.
An empty space matters when you have a parent. It gives some structural difference. But it doesn't matter if you don't have a parent. So for the root, we have $$$(children)!$$$, and for others we have $$$(children+1)!$$$.
So what now?
Since these options are mutually independent, they have to be multiplied with each other. Thus all you have to do is multiply all these and you've the answer.
One more thing to do. Now you've got the total number of different structures. But do notice that each structure is present $$$n$$$ times. The ordering is the same, but they've just rotated it. So, you have to multiply your answer by $$$n$$$ too in the end.
Do not forget to do the MOD though.
Here is my submission. I hope this helps.











Awesome Explaination!!