| Codeforces Round 676 (Div. 2) |
|---|
| Finished |
Lindsey Buckingham told Stevie Nicks "Go your own way". Nicks is now sad and wants to go away as quickly as possible, but she lives in a 2D hexagonal world.
Consider a hexagonal tiling of the plane as on the picture below.

Nicks wishes to go from the cell marked $$$(0, 0)$$$ to a certain cell given by the coordinates. She may go from a hexagon to any of its six neighbors you want, but there is a cost associated with each of them. The costs depend only on the direction in which you travel. Going from $$$(0, 0)$$$ to $$$(1, 1)$$$ will take the exact same cost as going from $$$(-2, -1)$$$ to $$$(-1, 0)$$$. The costs are given in the input in the order $$$c_1$$$, $$$c_2$$$, $$$c_3$$$, $$$c_4$$$, $$$c_5$$$, $$$c_6$$$ as in the picture below.
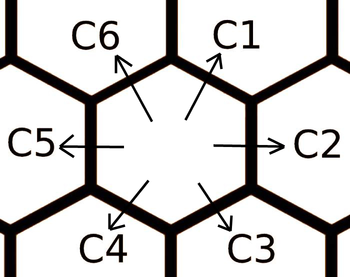
Print the smallest cost of a path from the origin which has coordinates $$$(0, 0)$$$ to the given cell.
Each test contains multiple test cases. The first line contains the number of test cases $$$t$$$ ($$$1 \le t \le 10^{4}$$$). Description of the test cases follows.
The first line of each test case contains two integers $$$x$$$ and $$$y$$$ ($$$-10^{9} \le x, y \le 10^{9}$$$) representing the coordinates of the target hexagon.
The second line of each test case contains six integers $$$c_1$$$, $$$c_2$$$, $$$c_3$$$, $$$c_4$$$, $$$c_5$$$, $$$c_6$$$ ($$$1 \le c_1, c_2, c_3, c_4, c_5, c_6 \le 10^{9}$$$) representing the six costs of the making one step in a particular direction (refer to the picture above to see which edge is for each value).
For each testcase output the smallest cost of a path from the origin to the given cell.
2 -3 1 1 3 5 7 9 11 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000 1000000000
18 1000000000000000000
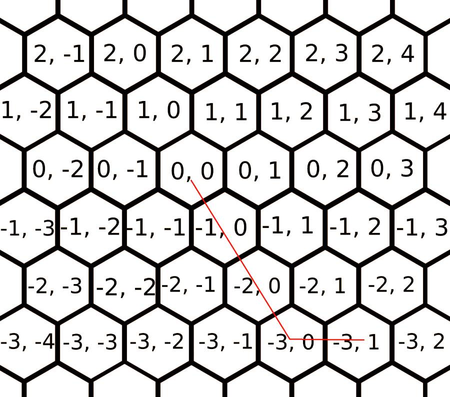
The picture below shows the solution for the first sample. The cost $$$18$$$ is reached by taking $$$c_3$$$ 3 times and $$$c_2$$$ once, amounting to $$$5+5+5+3=18$$$.
| Name |
|---|




