| Good Bye 2020 |
|---|
| Закончено |
Вы вероятно слышали про двенадцать подвигов Геракла, однако знаете ли вы про тринадцатый? Принято считать, что ему потребовалась дюжина лет, чтобы выполнить двенадцать подвигов, то есть в среднем год, чтобы выполнить каждый из них. Поскольку в наши дни время течет быстрее, у вас есть минуты, а не месяцы, чтобы решить эту задачу. Справитесь ли вы?
В этой задаче вам дано дерево с $$$n$$$ вершинами, каждая из которых имеет вес. Дерево — это связный граф с $$$n - 1$$$ ребром.
Определим $$$k$$$-раскраску дерева как назначение одного из $$$k$$$ цветов каждому из его ребер. Обратите внимание, что вы не обязаны использовать все $$$k$$$ цветов.
Подграф цвета $$$x$$$ состоит из тех ребер исходного графа, которым был назначен цвет $$$x$$$, и только тех вершин, которые смежны с хотя бы одним из таких ребер. Поэтому в таком подграфе нет вершин степени $$$0$$$.
Весом компоненты связности назовем сумму весов её вершин. Весом подграфа назовем максимальный из весов компонент связности этого подграфа. Вес пустого подграфа будем считать равным $$$0$$$.
Определим вес $$$k$$$-раскраски как сумму весов подграфов всех $$$k$$$ цветов. Дано дерево, для каждого $$$k$$$ от $$$1$$$ до $$$n - 1$$$ вычислите максимальный возможный вес $$$k$$$-раскраски.
Во входных данных находятся несколько (не меньше одного) наборов входных данных. В первой строке дано одно целое число $$$t$$$ ($$$1 \leq t \leq 10^5$$$), обозначающее количество наборов входных данных. Затем даны $$$t$$$ наборов входных данных.
В первой строке каждого набора входных данных дано одно целое число $$$n$$$ ($$$2 \leq n \leq 10^5$$$). Во второй строке дано $$$n$$$ целых чисел $$$w_1, w_2, \dots, w_n$$$ ($$$0 \leq w_i \leq 10^9$$$), $$$w_i$$$ равно весу $$$i$$$-й вершины. В следующих $$$n - 1$$$ строках, дано по два целых числа $$$u$$$, $$$v$$$ ($$$1 \leq u,v \leq n$$$), обозначающих ребро между вершинами $$$u$$$ и $$$v$$$. Гарантируется, что эти ребра описывают дерево.
Сумма $$$n$$$ по всем наборам входных данных не превышает $$$2 \cdot 10^5$$$.
Для каждого набора входных данных в отдельной строке выведите $$$n - 1$$$ целое число, где $$$i$$$-е число должно равняться максимальному весу $$$i$$$-раскраски дерева.
4 4 3 5 4 6 2 1 3 1 4 3 2 21 32 2 1 6 20 13 17 13 13 11 2 1 3 1 4 1 5 1 6 1 4 10 6 6 6 1 2 2 3 4 1
18 22 25 53 87 107 127 147 167 28 38 44
Оптимальные $$$k$$$-раскраски дерева из первого набора входных данных следующие:
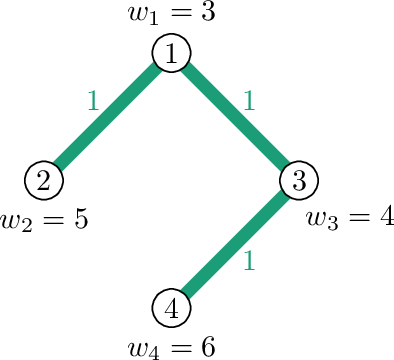
В $$$1$$$-раскраске все ребра имеют одинаковый цвет. Подграф цвета $$$1$$$ содержит все ребра и вершины исходного графа. Поэтому его вес равен $$$3 + 5 + 4 + 6 = 18$$$.
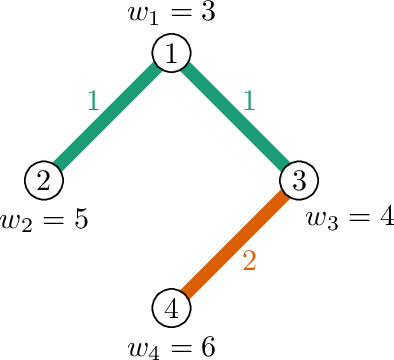
В оптимальной $$$2$$$-раскраске ребрам $$$(2, 1)$$$ и $$$(3,1)$$$ назначен цвет $$$1$$$. Ребру $$$(4, 3)$$$ — цвет $$$2$$$. Подграф цвета $$$1$$$ состоит из одной компоненты связности (вершины $$$1, 2, 3$$$) и его вес равен $$$3 + 5 + 4 = 12$$$. Подграф цвета $$$2$$$ состоит из двух вершин и одного ребра. Его вес равен $$$4 + 6 = 10$$$.
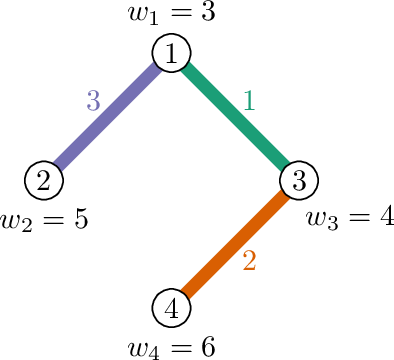
В оптимальной $$$3$$$-раскраске всем ребрам назначены разные цвета. Поэтому подграф каждого цвета содержит одно ребро. Их веса следующие: $$$3 + 4 = 7$$$, $$$4 + 6 = 10$$$, $$$3 + 5 = 8$$$.
| Название |
|---|




