| Codeforces Round 715 (Div. 1) |
|---|
| Finished |
As a teacher, Riko Hakozaki often needs to help her students with problems from various subjects. Today, she is asked a programming task which goes as follows.
You are given an undirected complete graph with $$$n$$$ nodes, where some edges are pre-assigned with a positive weight while the rest aren't. You need to assign all unassigned edges with non-negative weights so that in the resulting fully-assigned complete graph the XOR sum of all weights would be equal to $$$0$$$.
Define the ugliness of a fully-assigned complete graph the weight of its minimum spanning tree, where the weight of a spanning tree equals the sum of weights of its edges. You need to assign the weights so that the ugliness of the resulting graph is as small as possible.
As a reminder, an undirected complete graph with $$$n$$$ nodes contains all edges $$$(u, v)$$$ with $$$1 \le u < v \le n$$$; such a graph has $$$\frac{n(n-1)}{2}$$$ edges.
She is not sure how to solve this problem, so she asks you to solve it for her.
The first line contains two integers $$$n$$$ and $$$m$$$ ($$$2 \le n \le 2 \cdot 10^5$$$, $$$0 \le m \le \min(2 \cdot 10^5, \frac{n(n-1)}{2} - 1)$$$) — the number of nodes and the number of pre-assigned edges. The inputs are given so that there is at least one unassigned edge.
The $$$i$$$-th of the following $$$m$$$ lines contains three integers $$$u_i$$$, $$$v_i$$$, and $$$w_i$$$ ($$$1 \le u_i, v_i \le n$$$, $$$u \ne v$$$, $$$1 \le w_i < 2^{30}$$$), representing the edge from $$$u_i$$$ to $$$v_i$$$ has been pre-assigned with the weight $$$w_i$$$. No edge appears in the input more than once.
Print on one line one integer — the minimum ugliness among all weight assignments with XOR sum equal to $$$0$$$.
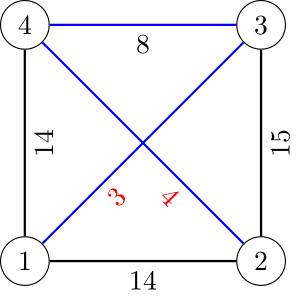
4 4 2 1 14 1 4 14 3 2 15 4 3 8
15
6 6 3 6 4 2 4 1 4 5 7 3 4 10 3 5 1 5 2 15
0
5 6 2 3 11 5 3 7 1 4 10 2 4 14 4 3 8 2 5 6
6
The following image showcases the first test case. The black weights are pre-assigned from the statement, the red weights are assigned by us, and the minimum spanning tree is denoted by the blue edges.
| Name |
|---|




