| Codeforces Round 715 (Div. 1) |
|---|
| Finished |
Touko's favorite sequence of numbers is a permutation $$$a_1, a_2, \dots, a_n$$$ of $$$1, 2, \dots, n$$$, and she wants some collection of permutations that are similar to her favorite permutation.
She has a collection of $$$q$$$ intervals of the form $$$[l_i, r_i]$$$ with $$$1 \le l_i \le r_i \le n$$$. To create permutations that are similar to her favorite permutation, she coined the following definition:
- A permutation $$$b_1, b_2, \dots, b_n$$$ allows an interval $$$[l', r']$$$ to holds its shape if for any pair of integers $$$(x, y)$$$ such that $$$l' \le x < y \le r'$$$, we have $$$b_x < b_y$$$ if and only if $$$a_x < a_y$$$.
- A permutation $$$b_1, b_2, \dots, b_n$$$ is $$$k$$$-similar if $$$b$$$ allows all intervals $$$[l_i, r_i]$$$ for all $$$1 \le i \le k$$$ to hold their shapes.
Yuu wants to figure out all $$$k$$$-similar permutations for Touko, but it turns out this is a very hard task; instead, Yuu will encode the set of all $$$k$$$-similar permutations with directed acylic graphs (DAG). Yuu also coined the following definitions for herself:
- A permutation $$$b_1, b_2, \dots, b_n$$$ satisfies a DAG $$$G'$$$ if for all edge $$$u \to v$$$ in $$$G'$$$, we must have $$$b_u < b_v$$$.
- A $$$k$$$-encoding is a DAG $$$G_k$$$ on the set of vertices $$$1, 2, \dots, n$$$ such that a permutation $$$b_1, b_2, \dots, b_n$$$ satisfies $$$G_k$$$ if and only if $$$b$$$ is $$$k$$$-similar.
Since Yuu is free today, she wants to figure out the minimum number of edges among all $$$k$$$-encodings for each $$$k$$$ from $$$1$$$ to $$$q$$$.
The first line contains two integers $$$n$$$ and $$$q$$$ ($$$1 \le n \le 25\,000$$$, $$$1 \le q \le 100\,000$$$).
The second line contains $$$n$$$ integers $$$a_1, a_2, \dots, a_n$$$ which form a permutation of $$$1, 2, \dots, n$$$.
The $$$i$$$-th of the following $$$q$$$ lines contains two integers $$$l_i$$$ and $$$r_i$$$. ($$$1 \le l_i \le r_i \le n$$$).
Print $$$q$$$ lines. The $$$k$$$-th of them should contain a single integer — The minimum number of edges among all $$$k$$$-encodings.
4 3 2 4 1 3 1 3 2 4 1 4
2 4 3
8 4 3 7 4 8 1 5 2 6 3 6 1 6 3 8 1 8
3 5 9 7
10 10 10 5 1 2 7 3 9 4 6 8 2 2 4 5 6 8 4 10 4 4 2 7 2 2 7 8 3 7 2 10
0 1 3 6 6 9 9 9 9 8
For the first test case:
- All $$$1$$$-similar permutations must allow the interval $$$[1, 3]$$$ to hold its shape. Therefore, the set of all $$$1$$$-similar permutations is $$$\{[3, 4, 2, 1], [3, 4, 1, 2], [2, 4, 1, 3], [2, 3, 1, 4]\}$$$. The optimal encoding of these permutations is

- All $$$2$$$-similar permutations must allow the intervals $$$[1, 3]$$$ and $$$[2, 4]$$$ to hold their shapes. Therefore, the set of all $$$2$$$-similar permutations is $$$\{[3, 4, 1, 2], [2, 4, 1, 3]\}$$$. The optimal encoding of these permutations is

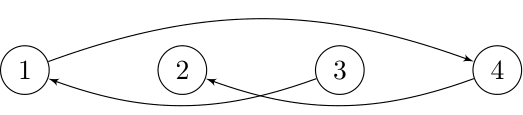
- All $$$3$$$-similar permutations must allow the intervals $$$[1, 3]$$$, $$$[2, 4]$$$, and $$$[1, 4]$$$ to hold their shapes. Therefore, the set of all $$$3$$$-similar permutations only includes $$$[2, 4, 1, 3]$$$. The optimal encoding of this permutation is
| Name |
|---|




