| Codeforces Round 786 (Div. 3) |
|---|
| Закончено |
Дан ориентированный ацикличный граф, состоящий из $$$n$$$ вершин и $$$m$$$ ребер. Вершины пронумерованы от $$$1$$$ до $$$n$$$. В графе нет кратных ребер и петель.
Пусть $$$\mathit{in}_v$$$ будет количеством входящих ребер (степень входа), а $$$\mathit{out}_v$$$ будет количеством исходящих ребер (степень исхода) вершины $$$v$$$.
Требуется удалить некоторые ребра из графа. Пусть новые степени будут $$$\mathit{in'}_v$$$ и $$$\mathit{out'}_v$$$.
Разрешается удалять ребра, только если выполняются следующие условия для каждой вершины $$$v$$$:
- $$$\mathit{in'}_v < \mathit{in}_v$$$ or $$$\mathit{in'}_v = \mathit{in}_v = 0$$$;
- $$$\mathit{out'}_v < \mathit{out}_v$$$ or $$$\mathit{out'}_v = \mathit{out}_v = 0$$$.
Назовем множество вершин $$$S$$$ красивым, если для каждой пары вершин $$$v$$$ и $$$u$$$ ($$$v \neq u$$$), таких, что $$$v \in S$$$ и $$$u \in S$$$, существует путь либо из $$$v$$$ в $$$u$$$, либо из $$$u$$$ в $$$v$$$ по неудаленным ребрам.
Какой максимальный возможный размер красивого множества $$$S$$$ после того, как вы удалите некоторые ребра из графа, а степени входа и исхода всех вершин либо уменьшатся, либо останутся равны $$$0$$$?
В первой строке записаны два целых числа $$$n$$$ и $$$m$$$ ($$$1 \le n \le 2 \cdot 10^5$$$; $$$0 \le m \le 2 \cdot 10^5$$$) — количество вершин и количество ребер графа.
В каждой из следующих $$$m$$$ строк записаны два целых числа $$$v$$$ и $$$u$$$ ($$$1 \le v, u \le n$$$; $$$v \neq u$$$) — описание ребра.
Данные ребра образуют корректный ориентированный ацикличный граф. Кратные ребра отсутствуют.
Выведите одно целое число — максимальный возможный размер красивого множества $$$S$$$ после того, как вы удалите некоторые ребра из графа, а степени входа и исхода всех вершин либо уменьшатся, либо останутся равны $$$0$$$.
3 3 1 2 2 3 1 3
2
5 0
1
7 8 7 1 1 3 6 2 2 3 7 2 2 4 7 3 6 3
3
В первом примере можно удалить ребра $$$(1, 2)$$$ и $$$(2, 3)$$$. $$$\mathit{in} = [0, 1, 2]$$$, $$$\mathit{out} = [2, 1, 0]$$$. $$$\mathit{in'} = [0, 0, 1]$$$, $$$\mathit{out'} = [1, 0, 0]$$$. Можно видеть, что для всех $$$v$$$ условия выполняются. Максимальное красивое множество $$$S$$$ образовано вершинами $$$1$$$ и $$$3$$$. Они все еще соединены ребром напрямую, поэтому между ними есть путь.
Во втором примере нет ребер. Так как все $$$\mathit{in}_v$$$ и $$$\mathit{out}_v$$$ равны $$$0$$$, оставить граф с нулем ребер разрешено. Есть $$$5$$$ красивых множеств, в каждом содержится одна вершина. Поэтому максимальный размер множества равен $$$1$$$.
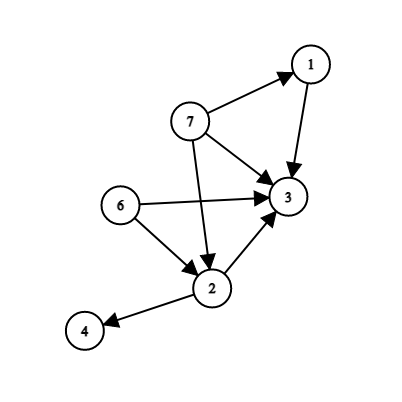
В третьем примере можно удалить ребра $$$(7, 1)$$$, $$$(2, 4)$$$, $$$(1, 3)$$$ и $$$(6, 2)$$$. Максимальное красивое множество $$$S = \{7, 3, 2\}$$$. Можно еще удалить ребро $$$(7, 3)$$$, и ответ не изменится.
Изображение графа с третьего примера:
| Название |
|---|




