| Codeforces Round 809 (Div. 2) |
|---|
| Закончено |
Вам дан связный неориентированный граф из $$$n$$$ вершин и $$$m$$$ рёбер. Вершины графа пронумерованы целыми числами от $$$1$$$ до $$$n$$$, а рёбра графа пронумерованы целыми числами от $$$1$$$ до $$$m$$$.
Вам предстоит ответить на $$$q$$$ запросов, каждый из которых состоит из двух чисел $$$l$$$ и $$$r$$$. Ответом на запрос является наименьшее неотрицательное число $$$k$$$, для которого выполняется следующее условие:
- для всех пар чисел $$$(a, b)$$$ таких, что $$$l\le a\le b\le r$$$, вершины $$$a$$$ и $$$b$$$ достижимы друг из друга по пути, проходящему только по первым $$$k$$$ рёбрам (то есть в пути могут встречаться только рёбра $$$1, 2, \ldots, k$$$).
В первой строке задано одно целое число $$$t$$$ ($$$1\le t\le 1000$$$) — количество наборов входных данных. Далее следуют описания этих наборов.
В первой строке даны три числа $$$n$$$, $$$m$$$ и $$$q$$$ ($$$2\le n\le 10^5$$$, $$$1\le m, q\le 2\cdot 10^5$$$) — количество вершин, рёбер и запросов соответственно.
В каждой из следующих $$$m$$$ строк дано по два числа $$$u_i$$$ и $$$v_i$$$ ($$$1\le u_i, v_i\le n$$$) — концы $$$i$$$-го ребра.
Гарантируется, что заданный граф связный и в нём нет кратных рёбер и петель.
В каждой из следующих $$$q$$$ строк дано по два числа $$$l$$$ и $$$r$$$ ($$$1\le l\le r\le n$$$) — описания запросов.
Гарантируется, что сумма $$$n$$$ во всем наборам входных данных не превосходит $$$10^5$$$, сумма $$$m$$$ во всем наборам входных данных не превосходит $$$2\cdot 10^5$$$, сумма $$$q$$$ во всем наборам входных данных не превосходит $$$2\cdot 10^5$$$.
Для каждого набора входных данных выведите $$$q$$$ чисел — ответы на запросы.
32 1 21 21 11 25 5 51 21 32 43 43 51 43 42 22 53 53 2 11 32 31 3
0 1 3 3 0 5 5 2
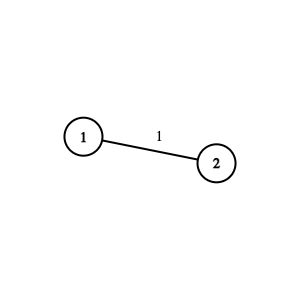 Граф из первого набора входных данных. Около ребра записан его номер.
Граф из первого набора входных данных. Около ребра записан его номер. В первом наборе входных данных граф состоит из $$$2$$$ вершин и одного ребра между вершинами $$$1$$$ и $$$2$$$.
В первом запросе $$$l=1$$$ и $$$r=1$$$. Вершина достижима сама из себя без использования рёбер, поэтому ответ на этот запрос равен $$$0$$$.
Во втором запросе $$$l=1$$$ и $$$r=2$$$. Вершины $$$1$$$ и $$$2$$$ достижимы друг из друга по пути $$$1 \longleftrightarrow 2$$$, состоящему только из первого ребра. В то же время невозможно добраться из вершины $$$1$$$ до вершины $$$2$$$, используя только первые $$$0$$$ рёбер. Поэтому ответ на запрос равен $$$1$$$.
 Граф из второго набора входных данных. Около рёбер записаны их номера.
Граф из второго набора входных данных. Около рёбер записаны их номера. Во втором наборе входных данных граф состоит из $$$5$$$ вершин и $$$5$$$ рёбер.
В первом запросе $$$l=1$$$ и $$$r=4$$$. Чтобы выполнить требуемое условие, достаточно использовать первые $$$3$$$ ребра:
- Вершины $$$1$$$ и $$$2$$$ достижимы друг из друга по пути $$$1 \longleftrightarrow 2$$$ (состоящему из ребра $$$1$$$).
- Вершины $$$1$$$ и $$$3$$$ достижимы друг из друга по пути $$$1 \longleftrightarrow 3$$$ (состоящему из ребра $$$2$$$).
- Вершины $$$1$$$ и $$$4$$$ достижимы друг из друга по пути $$$1 \longleftrightarrow 2 \longleftrightarrow 4$$$ (состоящему из рёбер $$$1$$$ и $$$3$$$).
- Вершины $$$2$$$ и $$$3$$$ достижимы друг из друга по пути $$$2 \longleftrightarrow 1 \longleftrightarrow 3$$$ (состоящему из рёбер $$$1$$$ и $$$2$$$).
- Вершины $$$2$$$ и $$$4$$$ достижимы друг из друга по пути $$$2 \longleftrightarrow 4$$$ (состоящему из ребра $$$3$$$).
- Вершины $$$3$$$ и $$$4$$$ достижимы друг из друга по пути $$$3 \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow 4$$$ (состоящему из рёбер $$$2$$$, $$$1$$$ и $$$3$$$).
Невозможно выполнить требуемое условие, используя меньше $$$3$$$ первых рёбер. Например, при использовании $$$2$$$ рёбер, невозможно добраться из вершины $$$1$$$ в вершину $$$4$$$. Поэтому ответ на запрос равен $$$3$$$.
Во втором запросе $$$l=3$$$ и $$$r=4$$$. Вершины $$$3$$$ и $$$4$$$ достижимы друг из друга по пути $$$3 \longleftrightarrow 1 \longleftrightarrow 2 \longleftrightarrow 4$$$ (состоящему из рёбер $$$2$$$, $$$1$$$ и $$$3$$$). При использовании меньшего числа первых рёбер вершины $$$3$$$ и $$$4$$$ не будут достижимы друг из друга.
| Название |
|---|




