| Good Bye 2022: 2023 is NEAR |
|---|
| Finished |
Imi has an undirected tree with $$$n$$$ vertices where edges are numbered from $$$1$$$ to $$$n-1$$$. The $$$i$$$-th edge connects vertices $$$u_i$$$ and $$$v_i$$$. There are also $$$k$$$ butterflies on the tree. Initially, the $$$i$$$-th butterfly is on vertex $$$a_i$$$. All values of $$$a$$$ are pairwise distinct.
Koxia plays a game as follows:
- For $$$i = 1, 2, \dots, n - 1$$$, Koxia set the direction of the $$$i$$$-th edge as $$$u_i \rightarrow v_i$$$ or $$$v_i \rightarrow u_i$$$ with equal probability.
- For $$$i = 1, 2, \dots, n - 1$$$, if a butterfly is on the initial vertex of $$$i$$$-th edge and there is no butterfly on the terminal vertex, then this butterfly flies to the terminal vertex. Note that operations are sequentially in order of $$$1, 2, \dots, n - 1$$$ instead of simultaneously.
- Koxia chooses two butterflies from the $$$k$$$ butterflies with equal probability from all possible $$$\frac{k(k-1)}{2}$$$ ways to select two butterflies, then she takes the distance$$$^\dagger$$$ between the two chosen vertices as her score.
Now, Koxia wants you to find the expected value of her score, modulo $$$998\,244\,353^\ddagger$$$.
$$$^\dagger$$$ The distance between two vertices on a tree is the number of edges on the (unique) simple path between them.
$$$^\ddagger$$$ Formally, let $$$M = 998\,244\,353$$$. It can be shown that the answer can be expressed as an irreducible fraction $$$\frac{p}{q}$$$, where $$$p$$$ and $$$q$$$ are integers and $$$q \not \equiv 0 \pmod{M}$$$. Output the integer equal to $$$p \cdot q^{-1} \bmod M$$$. In other words, output such an integer $$$x$$$ that $$$0 \le x < M$$$ and $$$x \cdot q \equiv p \pmod{M}$$$.
The first line contains two integers $$$n$$$, $$$k$$$ ($$$2 \leq k \leq n \leq 3 \cdot {10}^5$$$) — the size of the tree and the number of butterflies.
The second line contains $$$k$$$ integers $$$a_1, a_2, \dots, a_k$$$ ($$$1 \leq a_i \leq n$$$) — the initial position of butterflies. It's guaranteed that all positions are distinct.
The $$$i$$$-th line in following $$$n − 1$$$ lines contains two integers $$$u_i$$$, $$$v_i$$$ ($$$1 \leq u_i, v_i \leq n$$$, $$$u_i \neq v_i$$$) — the vertices the $$$i$$$-th edge connects.
It is guaranteed that the given edges form a tree.
Output a single integer — the expected value of Koxia's score, modulo $$$998\,244\,353$$$.
3 2 1 3 1 2 2 3
748683266
5 3 3 4 5 1 2 1 3 2 4 2 5
831870296
In the first test case, the tree is shown below. Vertices containing butterflies are noted as bold.
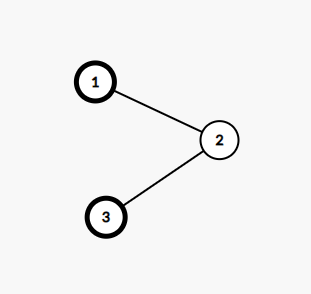
There are only $$$2$$$ butterflies so the choice of butterflies is fixed. Let's consider the following $$$4$$$ cases:
- Edges are $$$1 \rightarrow 2$$$ and $$$2 \rightarrow 3$$$: butterfly on vertex $$$1$$$ moves to vertex $$$2$$$, but butterfly on vertex $$$3$$$ doesn't move. The distance between vertices $$$2$$$ and $$$3$$$ is $$$1$$$.
- Edges are $$$1 \rightarrow 2$$$ and $$$3 \rightarrow 2$$$: butterfly on vertex $$$1$$$ moves to vertex $$$2$$$, but butterfly on vertex $$$3$$$ can't move to vertex $$$2$$$ because it's occupied. The distance between vertices $$$2$$$ and $$$3$$$ is $$$1$$$.
- Edges are $$$2 \rightarrow 1$$$ and $$$2 \rightarrow 3$$$: butterflies on both vertex $$$1$$$ and vertex $$$3$$$ don't move. The distance between vertices $$$1$$$ and $$$3$$$ is $$$2$$$.
- Edges are $$$2 \rightarrow 1$$$ and $$$3 \rightarrow 2$$$: butterfly on vertex $$$1$$$ doesn't move, but butterfly on vertex $$$3$$$ move to vertex $$$2$$$. The distance between vertices $$$1$$$ and $$$2$$$ is $$$1$$$.
Therefore, the expected value of Koxia's score is $$$\frac {1+1+2+1} {4} = \frac {5} {4}$$$, which is $$$748\,683\,266$$$ after modulo $$$998\,244\,353$$$.
In the second test case, the tree is shown below. Vertices containing butterflies are noted as bold. The expected value of Koxia's score is $$$\frac {11} {6}$$$, which is $$$831\,870\,296$$$ after modulo $$$998\,244\,353$$$.

| Name |
|---|




