| Hello 2024 |
|---|
| Закончено |
Жюри загадало секретное дерево с $$$n$$$ вершинами. $$$n-1$$$ ребро дерева пронумерованы от $$$1$$$ до $$$n-1$$$. Вы можете делать запросы следующих двух типов:
- Дать грейдеру массив $$$a$$$ из $$$n - 1$$$ положительных целых чисел. Для каждого ребра от $$$1$$$ до $$$n - 1$$$ вес ребра $$$i$$$ устанавливается равным $$$a_i$$$. Грейдер вернет длину диаметра$$$^\dagger$$$ дерева с данными весами.
- Дать грейдеру два индекса $$$1 \le a, b \le n - 1$$$. Грейдер вернет количество ребер между ребрами $$$a$$$ и $$$b$$$. Другими словами, если ребро $$$a$$$ соединяет $$$u_a$$$ и $$$v_a$$$, а ребро $$$b$$$ соединяет $$$u_b$$$ и $$$v_b$$$, то грейдер вернет $$$\min(\text{dist}(u_a, u_b), \text{dist}(v_a, u_b), \text{dist}(u_a, v_b), \text{dist}(v_a, v_b))$$$, где $$$\text{dist}(u, v)$$$ представляет собой количество ребер на пути между вершинами $$$u$$$ и $$$v$$$.
Найдите любое дерево, изоморфное$$$^\ddagger$$$ секретному дереву после не более чем $$$n$$$ запросов типа 1 и не более чем $$$n$$$ запросов типа 2 в любом порядке.
$$$^\dagger$$$ Расстояние между двумя вершинами равно сумме весов единственного простого пути, соединяющего их. Диаметр — это наибольшее из этих расстояний.
$$$^\ddagger$$$ Два дерева, состоящие из $$$n$$$ вершин каждое, называются изоморфными, если существует перестановка $$$p$$$, содержащая целые числа от $$$1$$$ до $$$n$$$, такая, что ребро ($$$u$$$, $$$v$$$) присутствует в первом дереве тогда и только тогда, когда ребро ($$$p_u$$$, $$$p_v$$$) присутствует во втором дереве.
Первая и единственная строка ввода содержит одно целое число $$$n$$$ ($$$3 \le n \le 1000$$$) — количество вершин в дереве.
Начните взаимодействие с чтения $$$n$$$.
Вам разрешается делать запросы следующим образом:
- «$$$\mathtt{?}\,1\,a_1\,a_2 \ldots a_{n-1}$$$» ($$$1 \le a_i \le 10^9$$$). Затем вы должны cчитать целое число $$$k$$$, которое представляет собой длину диаметра. Вы можете задать этот запрос не более $$$n$$$ раз.
- «$$$\mathtt{?}\,2\,a\,b$$$» ($$$1 \le a, b \le n - 1$$$). Затем вы должны прочитать целое число $$$k$$$, которое представляет собой количество ребер между ребрами $$$a$$$ и $$$b$$$. Вы можете задать этот запрос не более $$$n$$$ раз.
Если ваш запрос некорректен, программа немедленно завершится, и вы получите вердикт Неправильный ответ.
Чтобы вывести ответ, выведите «!» в единственной строке, за которой следует $$$n - 1$$$ строка, где строка $$$i$$$ содержит «$$$u_i\,v_i$$$» ($$$1 \le u_i, v_i \le n$$$), что означает, что для каждого $$$i$$$ от $$$1$$$ до $$$n-1$$$, существует ребро между $$$u_i$$$ и $$$v_i$$$.
После вывода запроса не забудьте вывести перевод строки и сбросить буфер вывода. В противном случае вы получите вердикт Решение «зависло». Для сброса буфера используйте:
- fflush(stdout) или cout.flush() в C++;
- System.out.flush() в Java;
- flush(output) в Pascal;
- stdout.flush() в Python;
- смотрите документацию для других языков.
Взломы
Первая строка содержит одно целое число $$$n$$$ ($$$3 \le n \le 1000$$$) — количество вершин в дереве.
Следующие $$$n - 1$$$ строк содержат по два целых числа $$$u_i, v_i$$$ ($$$1 \le u_i, v_i \le n$$$) — ребра дерева.
5 3 1 9 0
? 1 1 1 1 1 ? 2 1 3 ? 1 4 3 2 1 ? 2 4 2 ! 3 1 4 2 1 2 2 5
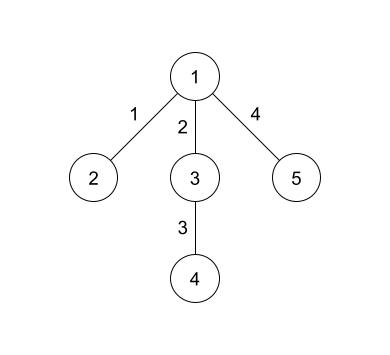
Секретное дерево в примере показано выше. Здесь числа на вершинах обозначают номер вершины, а числа на ребрах — номера ребер.

В первом запросе все ребра имеют вес $$$1$$$, поэтому диаметр имеет длину $$$3$$$, как показано на картинке.
Во втором запросе между ребрами $$$1$$$ и $$$3$$$ есть $$$1$$$ ребро.
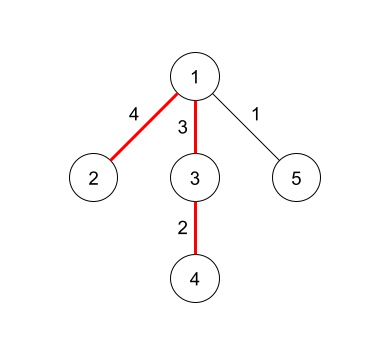
В третьем запросе диаметр равен $$$9$$$, если взять ребра $$$1$$$, $$$2$$$ и $$$3$$$.
В четвертом запросе между ребрами $$$4$$$ и $$$2$$$ нет ребер.
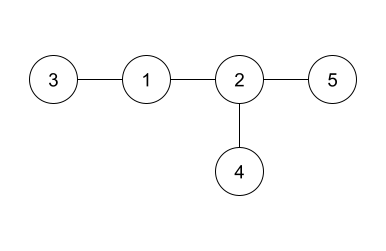
Ответ, приведенный в примере, показан на картинке выше. Поскольку он изоморфен секретному дереву, он принимается как правильный ответ. Обратите внимание, что ребра могут быть выведены в любом порядке.
| Название |
|---|




