| Codeforces Round 921 (Div. 1) |
|---|
| Закончено |
У вас есть квадратный лист бумаги со стороной длиной $$$1$$$ единица. За одну операцию вы складываете каждый угол квадрата к центру, образуя таким образом еще один квадрат со стороной длины $$$\dfrac{1}{\sqrt{2}}$$$ единицы. Взяв этот квадрат в качестве нового квадрата, вы выполняете операцию снова и повторяете этот процесс в общей сложности $$$N$$$ раз.
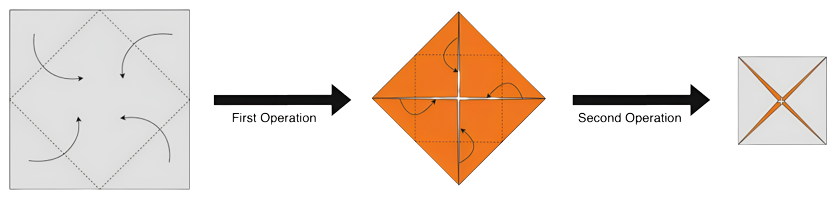 Выполнение операций для $$$N = 2$$$.
Выполнение операций для $$$N = 2$$$. После выполнения всех операций вы раскрываете бумагу той же стороной, с которой начали, и видите на ней некоторые линии сгиба. Каждая линия сгиба является одной из двух типов, горой или долиной, гора — это когда бумага складывается наружу, а долина — когда бумага складывается внутрь.
Вычислите сумму длин всех линий горных изгибов на бумаге и назовите ее $$$M$$$. Аналогично вычислите сумму длин для линий долин и назовите ее $$$V$$$. Необходимо найти значение $$$\dfrac{M}{V}$$$.
Можно доказать, что это значение можно представить в виде $$$A + B\sqrt{2}$$$, где $$$A$$$ и $$$B$$$ — рациональные числа. Пусть $$$B$$$ будет представлено в виде несократимой дроби $$$\dfrac{p}{q}$$$, ваша задача — напечатать $$$p*inv(q)$$$ по модулю $$$999\,999\,893$$$ (обратите внимание на необычный модуль), где $$$inv(q)$$$ — модуль, обратный к $$$q$$$.
Каждый тест содержит несколько тестовых случаев. Первая строка содержит количество тестов $$$t$$$ ($$$1 \leq t \leq 10^4$$$). Далее следует описание тестов.
Единственная строка каждого тестового случая содержит целое число $$$N$$$ ($$$1 \leq N \leq 10^9$$$), количество операций, которые вы выполняете на квадратной бумаге.
Для каждого тестового случая напечатайте на новой строке требуемый ответ.
3123
0 1 714285638
Синие линии на предоставленных рисунках представляют горные линии изгиба, а зеленые линии представляют долинные линии изгиба.
 | 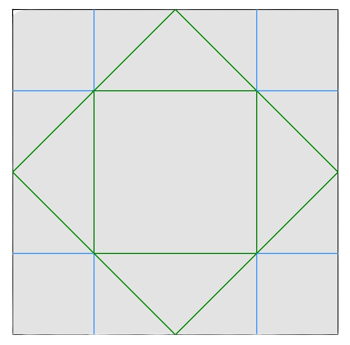 |
| Линии изгиба после $$$1$$$ операции $$$(\dfrac{M}{V} = 0)$$$. | Линии изгиба после $$$2$$$ операций $$$(\dfrac{M}{V} = \sqrt{2} - 1)$$$. |
| Название |
|---|




