I hope you enjoyed the round. Here is the editorial. Do provide your feedback on each problem so that we can improve upon them the next time.
2A. We Got Everything Covered!
Author: JaySharma1048576
The smallest length for such a string is $$$n\cdot k$$$.
The smallest length possible for such a string is $$$n\cdot k$$$.
To have the string $$$\texttt{aaa}\ldots\texttt{a}$$$ as a subsequence, you need to have at least $$$n$$$ characters in the string as $$$\texttt{a}$$$. Similarly for all $$$k$$$ different characters. So, that gives a total length of at least $$$n\cdot k$$$.
In fact, it is always possible to construct a string of length $$$n\cdot k$$$ that satisfies this property. One such string is $$$(a_1a_2a_3\ldots a_k)(a_1a_2a_3\ldots a_k)(a_1a_2a_3\ldots a_k)\ldots n$$$ times where $$$a_i$$$ is the $$$i^{th}$$$ letter of English alphabet. For example, the answer for $$$n=3,k=4$$$ can be $$$\texttt{abcdabcdabcd}$$$. It is not hard to see that the first letter of the subsequence can be from the first group of $$$k$$$ letters, second letter from the second group and so on.
#include <bits/stdc++.h>
using namespace std;
int main()
{
int tc;
cin >> tc;
while(tc--)
{
int n,k;
cin >> n >> k;
for(int i=0;i<n;i++)
for(char c='a';c<'a'+k;c++)
cout << c;
cout << '\n';
}
}
2B. A Balanced Problemset?
Author: JaySharma1048576
$$$GCD(a_1,a_2,a_3,\ldots,a_n) = GCD(a_1,a_1+a_2,a_1+a_2+a_3,\ldots,a_1+a_2+a_3+\ldots+a_n)$$$
The maximum GCD that can be achieved is always a divisor of $$$x$$$.
Let the difficulties of the $$$n$$$ sub-problems be $$$a_1,a_2,a_3,\ldots,a_n$$$. By properties of GCD, $$$GCD(a_1,a_2,a_3,\ldots,a_n)$$$ $$$= GCD(a_1,a_1+a_2,a_1+a_2+a_3,\ldots,a_1+a_2+a_3+\ldots+a_n)$$$ $$$= GCD(a_1,a_1+a_2,a_1+a_2+a_3,\ldots,x)$$$. So, the final answer will always be a divisor of $$$x$$$.
Now, consider a divisor $$$d$$$ of $$$x$$$. If $$$n\cdot d\leq x$$$, you can choose the difficulties of the sub-problems to be $$$d,d,d,\ldots,x-(n-1)d$$$ each of which is a multiple of $$$d$$$ and hence, the balance of this problemset will be $$$d$$$. Otherwise you cannot choose the difficulties of $$$n$$$ sub-problems such that each of them is a multiple of $$$d$$$.
Find the maximum $$$d$$$ for which this condition holds. This can be done in $$$\mathcal{O}(\sqrt{x})$$$ using trivial factorization.
#include <bits/stdc++.h>
using namespace std;
int main()
{
int tc;
cin >> tc;
while(tc--)
{
int x,n;
cin >> x >> n;
int ans = 1;
for(int i=1;i*i<=x;i++)
{
if(x%i==0)
{
if(n<=x/i)
ans=max(ans,i);
if(n<=i)
ans=max(ans,x/i);
}
}
cout << ans << '\n';
}
}
2C/1A. Did We Get Everything Covered?
Author: JaySharma1048576
Try to build the counter-case greedily.
While building the counter-case, it is always optimal to choose the first character as the one whose first index of occurrence in the given string is the highest.
We will try to construct a counter-case. If we can't the answer is YES otherwise NO.
We will greedily construct the counter-case. It is always optimal to choose the first character of our counter-case as the character (among the first $$$k$$$ English alphabets) whose first index of occurrence in $$$s$$$ is the highest. Add this character to our counter-case, remove the prefix up to this character from $$$s$$$ and repeat until the length of the counter-case reaches $$$n$$$ or we reach the end of $$$s$$$.
If the length of the counter-case is less than $$$n$$$, find a character which does not appear in the last remaining suffix of $$$s$$$. Keep adding this character to the counter-case until its length becomes $$$n$$$. This is a valid string which does not occur as a subsequence of $$$s$$$.
Otherwise, all possible strings of length $$$n$$$ formed using the first $$$k$$$ English alphabets occur as a subsequence of $$$s$$$.
#include <bits/stdc++.h>
using namespace std;
int main()
{
std::ios::sync_with_stdio(false); cin.tie(NULL);cout.tie(NULL);
int t;
cin>>t;
while(t--)
{
int n, k, m;
cin>>n>>k>>m;
string s;
cin>>s;
string res="";
bool found[k];
memset(found, false, sizeof(found));
int count=0;
for(char c:s)
{
if(res.size()==n)
break;
count+=(!found[c-'a']);
found[c-'a']=true;
if(count==k)
{
memset(found, false, sizeof(found));
count=0;
res+=c;
}
}
if(res.size()==n)
cout<<"YES\n";
else
{
cout<<"NO\n";
for(int i=0;i<k;i++)
{
if(!found[i])
{
while(res.size()<n)
res+=(char)('a'+i);
}
}
cout<<res<<"\n";
}
}
}
This problem is essentially "Implement the checker for Div. 2A". It was not among the problems that were initially proposed for the round. While preparing problem 2A, I realized that writing the checker in itself might be a more interesting problem compared to 2A.
2D. Good Trip
Author: yash_daga
Since expected value is linear, we can consider the contribution of initial friendship values and the contribution of increase in friendship values by repeated excursions independently.
Contribution of the initial friendship values will be $$$\dfrac{k\times \sum_{i=1}^{n}f_i}{\binom{n}{2}}$$$.
Now we can assume that there are $$$m$$$ pair of friends out of a total of $$$\binom{n}{2}$$$ pairs of students whose initial friendship value is $$$0$$$.
Since expected value is linear, we can consider the contribution of initial friendship values and the contribution of increase in friendship values by repeated excursions independently.
Let $$$d=\binom{n}{2}$$$ denote the total number of pairs of students that can be formed.
Contribution of the initial friendship values will be $$$s=\dfrac{k\cdot \sum_{i=1}^{n}f_i}{d}$$$.
Now, to calculate the contribution to the answer by the increase in friendship values due to excursions, for each pair of friends, it will be $$$\sum_{x=0}^{k}\dfrac{x(x-1)}{2}\cdot P(x)$$$ where $$$P(x)$$$ is the probability of a pair of friends to be selected for exactly $$$x$$$ out of the $$$k$$$ excursions which is given by $$$P(x)=\binom{k}{x}\cdot \bigg(\dfrac{1}{d}\bigg)^{x}\cdot \bigg(\dfrac{d-1}{d}\bigg)^{k-x}$$$.
Since the increase is uniform for all pair of friends, we just have to multiply this value by $$$m$$$ and add it to the answer.
The time complexity is $$$\mathcal{O}(m+k\log k)$$$ per test case.
#include <bits/stdc++.h>
#define int long long
#define IOS std::ios::sync_with_stdio(false); cin.tie(NULL);cout.tie(NULL);
#define mod 1000000007ll
using namespace std;
const long long N=200005, INF=2000000000000000000;
int power(int a, int b, int p)
{
if(b==0)
return 1;
if(a==0)
return 0;
int res=1;
a%=p;
while(b>0)
{
if(b&1)
res=(1ll*res*a)%p;
b>>=1;
a=(1ll*a*a)%p;
}
return res;
}
int fact[N],inv[N];
void pre()
{
fact[0]=1;
inv[0]=1;
for(int i=1;i<N;i++)
fact[i]=(i*fact[i-1])%mod;
for(int i=1;i<N;i++)
inv[i]=power(fact[i], mod-2, mod);
}
int nCr(int n, int r, int p)
{
if(r>n || r<0)
return 0;
if(n==r)
return 1;
if (r==0)
return 1;
return (((fact[n]*inv[r]) % p )*inv[n-r])%p;
}
int32_t main()
{
IOS;
pre();
int t;
cin>>t;
while(t--)
{
int n, m, k;
cin>>n>>m>>k;
int sum=0;
for(int i=0;i<m;i++)
{
int a, b, f;
cin>>a>>b>>f;
sum=(sum + f)%mod;
}
int den=((n*(n-1))/2ll)%mod;
int den_inv=power(den, mod-2, mod);
int base=(((sum*k)%mod)*den_inv)%mod;
int avg_inc=0;
for(int i=1;i<=k;i++)
{
// Extra sum added to ans if a particular pair of friends is picked i times.
int sum=((i*(i-1))/2ll)%mod;
int prob = (nCr(k, i, mod)*power(den_inv, i, mod))%mod;
// Probablity that a particular pair in unpicked for a given excursion.
int unpicked_prob = ((den-1)*den_inv)%mod;
// Probability that a particular pair is picked exactly i times.
prob=(prob * power(unpicked_prob, k-i, mod))%mod;
avg_inc = (avg_inc + (sum*prob)%mod)%mod;
}
int ans = (base + (m*avg_inc)%mod)%mod;
cout<<ans<<'\n';
}
}
2E/1B. Space Harbour
Author: yash_daga
Segment Tree with Lazy Propogation
We can maintain a segment tree of size $$$n$$$ which initially stores the cost of all the ships.
Now there are 2 types of updates when we add an harbour:
- The ships to the left of the new harbour have their cost decreased by a fixed amount.
- The ships to the right of the harbour have their cost changed by the value equivalent to product of distance from the harbour on their right (which remains unchanged) and the difference in values of the previous and new harbour to their left.
Let $$$n=8$$$ and there be harbours on point $$$1$$$ and $$$8$$$ with values $$$10$$$ and $$$15$$$ respectively.
Now we add a harbour at point $$$x=4$$$ with value $$$5$$$.
- Case 1: $$$(x=2, 3)$$$ Cost for both ships get decreased by $$$10 \times (8-4)$$$
- Case 2: $$$(x=5,6,7)$$$ Cost for the ships get increased by $$$(5-10) \times 3, (5-10) \times 2, (5-10) \times 1$$$ respectively.
There are multiple ways to handle both the updates simultaneously, a simple way would be to use a struct simulating an arithmetic progression. It can contain two values
- Base: Simply a value which has to be added to all values belonging to the segment.
- Difference: For each node of the segment, $$$dif \times dist$$$ will be added to the node, where $$$dist$$$ is the distance of node from the end of the segment.
Using summation of arithmetic progression we can make sure that the updates on Difference can be applied to an entire segment lazily. You can see the code for more details.
#include <bits/stdc++.h>
#define int long long
#define IOS std::ios::sync_with_stdio(false); cin.tie(NULL);cout.tie(NULL);
using namespace std;
const long long N=300005;
struct ap {
int base, dif;
};
ap add(ap a, ap b)
{
ap res;
res.base = a.base + b.base;
res.dif = a.dif + b.dif;
return res;
}
int convert(ap a, int n)
{
int res = (n*a.base);
res += ((n*(n-1))/2ll)*a.dif;
return res;
}
int st[4*N], cost[N];
ap lazy[4*N];
ap zero = {0, 0};
void propogate(int node, int l, int r)
{
st[node] += convert(lazy[node], r-l+1);
if(l!=r)
{
lazy[node*2+1] = add(lazy[node*2+1], lazy[node]);
int mid = (l+r)/2;
int rig = (r-mid);
lazy[node].base += (rig*lazy[node].dif);
lazy[node*2] = add(lazy[node*2], lazy[node]);
}
lazy[node] = zero;
}
void build(int node, int l, int r)
{
if(l==r)
{
st[node] = cost[l];
lazy[node] = zero;
return;
}
int mid=(l+r)/2;
build(node*2, l, mid);
build(node*2+1, mid+1, r);
st[node] = (st[node*2] + st[node*2+1]);
lazy[node] = zero;
return;
}
void update(int node, int l, int r, int x, int y, ap val)
{
if(lazy[node].base != 0 || lazy[node].dif != 0)
propogate(node, l, r);
if(y<x||x>r||y<l)
return;
if(l>=x&&r<=y)
{
st[node] += convert(val, r-l+1);
if(l!=r)
{
lazy[node*2+1] = add(lazy[node*2+1], val);
int mid = (l+r)/2;
int rig = (r-mid);
val.base += (rig*val.dif);
lazy[node*2] = add(lazy[node*2], val);
}
return;
}
int mid=(l+r)/2;
update(node*2+1, mid+1, r, x, y, val);
if(y>mid)
{
int rig = (min(y, r)-mid);
val.base += (rig*val.dif);
}
update(node*2, l, mid, x, y, val);
st[node] = st[node*2] + st[node*2+1];
return;
}
int query(int node, int l, int r, int x, int y)
{
if(lazy[node].base != 0 || lazy[node].dif != 0)
propogate(node, l, r);
if(y<x||y<l||x>r)
return 0;
if(l>=x&&r<=y)
return st[node];
int mid=(l+r)/2;
return query(node*2, l, mid, x, y) + query(node*2+1, mid+1, r, x, y);
}
int32_t main()
{
IOS;
int n, m, q;
cin>>n>>m>>q;
set <int> harbours;
int X[m], V[n+1];
for(int i=0;i<m;i++)
{
cin>>X[i];
harbours.insert(X[i]);
}
for(int i=0;i<m;i++)
{
int v;
cin>>v;
cost[X[i]] = v;
V[X[i]] = v;
}
for(int i=1;i<=n;i++)
{
if(cost[i] == 0)
cost[i] = cost[i-1];
}
int dist=0;
for(int i=n;i>0;i--)
{
if(harbours.find(i) != harbours.end())
dist=0;
else
dist++;
cost[i] *= dist;
}
build(1, 1, n);
while(q--)
{
int typ;
cin>>typ;
if(typ == 1)
{
int x, v;
cin>>x>>v;
V[x] = v;
auto it = harbours.lower_bound(x);
int nxt = (*it);
it--;
int prev = (*it);
ap lef = {(V[prev]*(x-nxt)), 0};
ap rig = {0, V[x]-V[prev]};
update(1, 1, n, prev+1, x, lef);
update(1, 1, n, x+1, nxt, rig);
harbours.insert(x);
}
else
{
int l, r;
cin>>l>>r;
cout<<query(1, 1, n, l, r)<<'\n';
}
}
}
2F/1C. Fractal Origami
Author: mexomerf
You need more math and less paper :)
The length of mountain crease lines and valley crease lines created in each operation is the same, except for the first operation.
Let there be an upside of the paper and a downside of the paper, initially the upside of the paper is facing up. With a little imagination, we can see that the mountain crease lines on the upside of the paper will be valley crease lines on the downside of the paper, and vice versa.
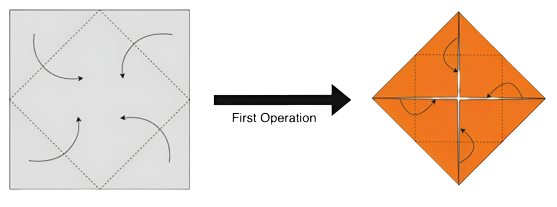
Grey is the upside and orange is the downside
After the first operation, what once was a single layer of square paper turns into a square with two overlapping layers of paper. The layer at the bottom has its upside facing up, and the layer at the top has its downside facing up.
After this first operation, whatever crease lines are formed on the upside of the bottom layer will be the same as the ones formed on the bottom layer of the top layer, which means when the paper is unfolded and the upside of the entire paper is facing up, the mountain crease lines and the valley crease lines created after the first operation will be equal.
Let $$$M$$$ be the length of mountain crease lines and $$$V$$$ be the length of valley crease lines after $$$N$$$ moves, and the side of the square paper is $$$1$$$.
Let $$$diff = V - M = $$$ Length of valley crease lines created in the first operation $$$ = 2\sqrt{2}$$$.
It is easy to calculate the total crease lines that are created (mountain and valley) in $$$N$$$ operations. It is the sum of a GP.
Let $$$sum = V + M = {\displaystyle\sum_{i = 1}^{N}}2^{i - 1}\cdot2\sqrt{2}\cdot{(\dfrac{1}{\sqrt{2}})}^{i - 1} = {\displaystyle\sum_{i = 1}^{N}}(\sqrt{2})^{i + 2}$$$
Now to find $$$\dfrac{M}{V}$$$, we use the age-old componendo and dividendo.
$$$\dfrac{M}{V} = \dfrac{sum - diff}{sum + diff}$$$
And then rationalize it to find the coefficient of $$$\sqrt{2}$$$.
The reason for the uncommon modulo in the problem is that the irrational part of $$$\dfrac{M}{V}$$$ is of the form $$$\dfrac{a\sqrt{2}}{b^2 - 2}$$$, where $$$a$$$ and $$$b$$$ are some integers. If there exists any $$$b$$$ such that $$$b^2 \equiv 2 \pmod m$$$, then the denominator becomes $$$0$$$.
To avoid this situation, such a prime modulo $$$m$$$ was taken for which $$$2$$$ is not a quadratic residue modulo $$$m$$$. It can be seen that $$$999999893\bmod 8 = 5$$$ and so, the Legendre symbol $$$\bigg(\dfrac{2}{999999893}\bigg) = -1$$$ meaning that $$$2$$$ is a quadratic non-residue modulo $$$999999893$$$.
// library link: https://github.com/manan-grover/My-CP-Library/blob/main/library.cpp
#include <bits/stdc++.h>
#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace std;
using namespace __gnu_pbds;
#define asc(i,a,n) for(I i=a;i<n;i++)
#define dsc(i,a,n) for(I i=n-1;i>=a;i--)
#define forw(it,x) for(A it=(x).begin();it!=(x).end();it++)
#define bacw(it,x) for(A it=(x).rbegin();it!=(x).rend();it++)
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define lb(x) lower_bound(x)
#define ub(x) upper_bound(x)
#define fbo(x) find_by_order(x)
#define ook(x) order_of_key(x)
#define all(x) (x).begin(),(x).end()
#define sz(x) (I)((x).size())
#define clr(x) (x).clear()
#define U unsigned
#define I long long int
#define S string
#define C char
#define D long double
#define A auto
#define B bool
#define CM(x) complex<x>
#define V(x) vector<x>
#define P(x,y) pair<x,y>
#define OS(x) set<x>
#define US(x) unordered_set<x>
#define OMS(x) multiset<x>
#define UMS(x) unordered_multiset<x>
#define OM(x,y) map<x,y>
#define UM(x,y) unordered_map<x,y>
#define OMM(x,y) multimap<x,y>
#define UMM(x,y) unordered_multimap<x,y>
#define BS(x) bitset<x>
#define L(x) list<x>
#define Q(x) queue<x>
#define PBS(x) tree<x,null_type,less<I>,rb_tree_tag,tree_order_statistics_node_update>
#define PBM(x,y) tree<x,y,less<I>,rb_tree_tag,tree_order_statistics_node_update>
#define pi (D)acos(-1)
#define md 999999893
#define rnd randGen(rng)
I modex(I a,I b,I m){
a=a%m;
if(b==0){
return 1;
}
I temp=modex(a,b/2,m);
temp=(temp*temp)%m;
if(b%2){
temp=(temp*a)%m;
}
return temp;
}
I mod(I a,I b,I m){
a=a%m;
b=b%m;
I c=__gcd(a,b);
a=a/c;
b=b/c;
c=modex(b,m-2,m);
return (a*c)%m;
}
int main(){
mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count());
uniform_int_distribution<I> randGen;
ios_base::sync_with_stdio(false);cin.tie(NULL);cout.tie(NULL);
#ifndef ONLINE_JUDGE
freopen("input.txt", "r", stdin);
freopen("out04.txt", "w", stdout);
#endif
I temp=md;
I t;
cin>>t;
while(t--){
I n;
cin>>n;
I b=modex(2,n/2,md)-1;
I a;
if(n%2){
a=modex(2,n/2+1,md)-1;
}else{
a=modex(2,n/2,md)-1;
}
I temp=(a+1)*(a+1);
temp%=md;
temp-=2*b*b;
temp%=md;
I ans=mod(2*b,temp,md);
ans+=md;
ans%=md;
cout<<ans<<"\n";
}
return 0;
}
1D. Balanced Subsequences
Author: yash_daga
Consider a function $$$f(n, m, k)$$$ which returns the number of permutations such that length of longest regular bracket subsequence is at most $$$2 \cdot k$$$ where $$$n$$$ is the number of '(' and $$$m$$$ is the number of ')'.
Answer to the problem is $$$f(n, m, k) - f(n, m, k-1)$$$
Now to compute $$$f(n, m, k)$$$, we can consider the following cases:
Case 1: $$$k \ge min(n, m)\rightarrow$$$ Here, the answer is $$${n+m} \choose {m}$$$, since none of the strings can have a subsequence of length greater than $$$k$$$.
Case 2: $$$k < min(n, m)\rightarrow$$$ Here we can write $$$f(n, m, k) = f(n-1, m, k-1) + f(n, m-1, k)$$$ since all strings will either start with:
a) ')' $$$\rightarrow$$$ Here, count is equal to $$$f(n, m-1, k)$$$.
b) '(' $$$\rightarrow$$$ Here, count is equal to $$$f(n-1, m, k-1)$$$, the first opening bracket will always add $$$1$$$ to the optimal subsequence length because all strings where each of the $$$m$$$ ')' is paired to some '(' don't contribute to the count since $$$k<m$$$.
After this recurrence relation we have 2 base cases:
- $$$k=0\rightarrow$$$ Here, count is $$$1$$$ which can also be written as $$${n+m} \choose {k}$$$.
- $$$k=min(n, m)\rightarrow$$$ Here, count is $$${n+m} \choose {m}$$$ (as proved in Case 1) which can also be written as $$${n+m} \choose {k}$$$.
Now using induction we can prove that the value of $$$f(n, m, k)$$$ for Case 2 is $$${n+m} \choose {k}$$$.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const long long N=4005, mod=1000000007;
int power(int a, int b, int p)
{
if(a==0)
return 0;
int res=1;
a%=p;
while(b>0)
{
if(b&1)
res=(1ll*res*a)%p;
b>>=1;
a=(1ll*a*a)%p;
}
return res;
}
int fact[N], inv[N];
void pre()
{
fact[0]=inv[0]=1;
for(int i=1;i<N;i++)
fact[i]=(fact[i-1]*i)%mod;
for(int i=1;i<N;i++)
inv[i]=power(fact[i], mod-2, mod);
}
int nCr(int n, int r)
{
if(min(n, r)<0 || r>n)
return 0;
if(n==r)
return 1;
return (((fact[n]*inv[r])%mod)*inv[n-r])%mod;
}
int f(int n, int m, int k)
{
if(k>=min(n, m))
return nCr(n+m, m);
return nCr(n+m, k);
}
int32_t main()
{
pre();
int t;
cin>>t;
while(t--)
{
int n, m, k;
cin>>n>>m>>k;
cout<<(f(n, m, k) - f(n, m, k-1) + mod)%mod<<"\n";
}
}
1E. Paper Cutting Again
Author: yash_daga
Can you solve it for $$$k=2$$$?
Using linearity of expectation, we can say that expected number of cuts is same as sum of probability of each line being cut and for $$$k=2$$$, we need to cut the paper until we achieve a $$$1 \times 1$$$ piece of paper.
Probability of each horizontal line being cut is $$$\dfrac {1}{count \thinspace of \thinspace lines \thinspace above \thinspace it + 1}$$$ Probability of each vertical line being cut is $$$\dfrac {1}{count \thinspace of \thinspace lines \thinspace left \thinspace to \thinspace it + 1}$$$
Now for $$$k=2$$$ we just have to calculate the sum of all these probabilities.
For the given problem we can solve it by dividing it into 4 cases:
Only Vertical Cuts:
Let the largest integer $$$y$$$ for which $$$n\cdot y<k$$$ be $$$reqv$$$.
The probability of achieving the goal using only vertical cuts is $$$\frac{reqv}{reqv+n-1}$$$ since one of the $$$reqv$$$ lines needs to be cut before all the horizontal lines. Now we will multiply this with the sum of conditional probabilities for each of the vertical line.
Sum of conditional probabilities of being cut for all lines from $$$1$$$ to $$$reqv$$$ is exactly $$$1$$$, since for area to be smaller than $$$k$$$, one of them needs to be cut and as soon as one is cut, the area becomes less than $$$k$$$ so no further cuts are required. Now for the lines from $$$reqv+1$$$ to $$$m-1$$$, their conditional probabilities will form the following harmonic progression:
$$$\frac{1}{n+reqv} + \frac{1}{n+reqv+1} + .... + \frac{1}{n+m-2}$$$
This is due to the fact that for a line to be cut it needs to occur before all horizontal lines and all vertical lines smaller than it.Case with only horizontal cuts can be handled similarly.
Case when the overall last cut is a horizontal one and there is at least one vertical cut:
For this, we iterate over the last cut among all the vertical cuts.
Let the last vertical cut be $$$x$$$. We now find the largest $$$y$$$ such that $$$(y\cdot x)<k$$$. Let this value be $$$reqh$$$.
The objective can be achieved using this case if the vertical line $$$x$$$ occurs before all the horizontal lines from $$$1$$$ to $$$reqh$$$ and all the vertical lines from $$$1$$$ to $$$x-1$$$, and after that any one of the horizontal line from $$$1$$$ to $$$reqh$$$ occur before all the vertical lines from $$$1$$$ to $$$x-1$$$.
The probability of this happening is $$$\frac{1}{x+reqh}\times\frac{reqh}{reqh+x-1}$$$.
Now we just add the the conditional probabilities of being cut for every line and multiply this with the above probability to find the contribution of this case to the final answer.
a. Firstly the conditional probability of the vertical line $$$x$$$ being cut is $$$1$$$.
b. The sum of conditional probabilities for horizontal lines $$$1$$$ to $$$reqh$$$ is also $$$1$$$.
The order of the first $$$x$$$ vertical cuts and the first $$$reqh$$$ horizontal cuts for the given case would look like:
$$$x_v$$$, $$$y1_h$$$, ($$$(x-1)$$$ vertical lines and $$$(reqh-1)$$$ horizontal lines in any relative ordering) [Total $$$x+reqh$$$ elements in the sequence].
$$$x_v$$$ denotes the $$$x^{th}$$$ vertical cut.
$$$y1_h$$$ denotes the horizontal cut which occurs first among all the first $$$reqh$$$ horizontal cuts.
c. Vertical cuts from $$$x+1$$$ to $$$m-1$$$:
For the $$$(x+1)^{th}$$$ cut, we can look at this like it needs to occur before the $$$x^{th}$$$ vertical cut (or it has one gap in the sequence to choose from a total of $$$(x+reqh+1)$$$ gaps).
So the probability is $$$\frac{1}{x+reqh+1}$$$.
For the $$$(x+2)^{th}$$$ cut, we can first place the $$$(x+2)^{th}$$$ cut with probability $$$\frac{1}{x+reqh+1}$$$ now we need to place the $$$(x+1)^{th}$$$ cut after of this which will happen with the probability of $$$\frac{x+reqh+1}{x+reqh+2}$$$.
So the overall probability is the product i.e., $$$\frac{1}{x+reqh+2}$$$.
Similarly, the probability for $$$(x+i)^{th}$$$ cut is $$$\frac{1}{x+reqh+i}$$$.
The sum of this Harmonic Progression can be computed in $$$\mathcal{O}(1)$$$ using pre computation.
d. Horizontal cuts from $$$reqh+1$$$ to $$$n-1$$$ (Trickiest Case imo)
Let us see the case for the $$$(reqh+1)^{th}$$$ cut $$$\rightarrow$$$ It has $$$2$$$ optimal gaps (before $$$x_v$$$ and the gap between $$$x_v$$$ and $$$y1_h$$$) so the probability is $$$\frac{2}{x+reqh+1}$$$.
Now for finding the probability for $$$(reqh+i)^{th}$$$ cut, we first place this cut into one of the $$$2$$$ gaps and handle both cases separately.
Gap before $$$x_v$$$: this case is similar to case 3c and the answer is just $$$\frac{1}{x+reqh+i}$$$.
Gap between $$$x_v$$$ and $$$y1_h$$$. Here we again have to ensure that all lines from $$$reqh+1$$$ to $$$reqh+i-1$$$ occur after $$$reqh+i$$$.
So we multiply $$$\frac{reqh+x}{reqh+x+2}\times\frac{reqs+x+1}{reqh+x+3}$$$ since after we place the $$$(reqh+i)^{th}$$$ cut, we have $$$(reqh+x)$$$ good gaps among a total of $$$(reqh+x+2)$$$ and so on for all the other lines we place (Their relative ordering does not matter since we are only concerned with $$$(reqh+i)^{th}$$$ cut).
The final term for $$$(reqh+i)^{th}$$$ cut occurs out to be: $$$\frac{x+reqh}{(x+reqh+i)\cdot(x+reqh+i-1)}$$$.
This forms a quadratic Harmonic Progression, the sum of which can be computed in $$$\mathcal{O}(1)$$$ using precomputation.Case when the overall last cut is a vertical one and there is at least one horizontal cut:
This case can be handled in a similar way as the previous case.
#include <bits/stdc++.h>
#define int long long
using namespace std;
const long long N=2000005, mod=1000000007;
int power(int a, int b, int p)
{
if(a==0)
return 0;
int res=1;
a%=p;
while(b>0)
{
if(b&1)
res=(1ll*res*a)%p;
b>>=1;
a=(1ll*a*a)%p;
}
return res;
}
int pref[N], inv[N], pref2[N], hp2[N];
// Returns (1/l + 1/(l+1) + ... + 1/r)
int cal(int l, int r)
{
if(l>r)
return 0;
return (pref[r]-pref[l-1]+mod)%mod;
}
// Returns (1/(l*(l+1)) + ... + 1/(r(r+1)))
int cal2(int l, int r)
{
if(l>r)
return 0;
return (pref2[r]-pref2[l-1]+mod)%mod;
}
void pre()
{
pref[0]=0;
pref2[0]=0;
for(int i=1;i<N;i++)
{
inv[i]=power(i, mod-2, mod);
pref[i]=(pref[i-1]+inv[i])%mod;
int mul2=(i*(i+1))%mod;
pref2[i]=(pref2[i-1] + power(mul2, mod-2, mod))%mod;
hp2[i]=((i*(i-1))%mod)%mod;
}
}
int solve2(int n, int m, int k)
{
if((n*m)<k)
return 0;
int ans=0;
int reqv=(k-1)/n;
if(reqv<m)
{
int prob=(reqv*inv[reqv+n-1])%mod;
int exp=(prob*(1ll + cal(n+reqv, m+n-2)))%mod;
ans=(ans + exp)%mod;
}
int reqh=(k-1)/m;
if(reqh<n)
{
int prob=(reqh*inv[reqh+m-1])%mod;
int exp=(prob*(1ll + cal(m+reqh, m+n-2)))%mod;
ans=(ans + exp)%mod;
}
for(int i=1;i<min(n, k);i++)
{
reqv=(k-1)/i;
if(reqv>=m)
continue;
int prob=(inv[i+reqv]*reqv)%mod;
prob=(prob*inv[i-1+reqv])%mod;
int num1=(hp2[i+reqv+1]*cal2(i+reqv, i+m-2))%mod;
int num2=((i+reqv+1)*cal(i+reqv+1, i+m-1))%mod;
int num=((num1+num2)*inv[i+reqv+1])%mod;
int exp=(prob*(2ll + cal(i+reqv+1, reqv+(n-1))+num))%mod;
ans=(ans + exp)%mod;
}
for(int i=1;i<min(m, k);i++)
{
reqh=(k-1)/i;
if(reqh>=n)
continue;
int prob=(inv[i+reqh]*reqh)%mod;
prob=(prob*inv[i-1+reqh])%mod;
// Sum for cases when the (reqh+i)th horizontal line occurs in the gap b/w x_v and y1_h
int num1=(hp2[i+reqh+1]*cal2(i+reqh, i+n-2))%mod;
// Sum for cases when the (reqh+i)th horizontal line occurs in the gap to the left of x_v
int num2=((i+reqh+1)*cal(i+reqh+1, i+n-1))%mod;
int num=((num1+num2)*inv[i+reqh+1])%mod;
int exp=(prob*(2ll + cal(i+reqh+1, reqh+(m-1))+num))%mod;
ans=(ans + exp)%mod;
}
return ans;
}
int32_t main()
{
pre();
int t;
cin>>t;
while(t--)
{
int n, m, k;
cin>>n>>m>>k;
cout<<solve2(n, m, k)<<"\n";
}
}
1F. Anti-Proxy Attendance
Author: JaySharma1048576
$$$\sqrt[4]{1.5}=1.1069$$$
Try to do a $$$3\rightarrow 2$$$ reduction in $$$4$$$ queries.
Try to do a $$$3\rightarrow 2$$$ reduction in such a way that if the middle part is eliminated $$$3$$$ queries are used otherwise $$$4$$$ queries are used.
Instead of dividing the search space into $$$3$$$ equal parts, divide it into parts having size $$$36\%$$$, $$$28\%$$$ and $$$36\%$$$.
There might be multiple strategies to solve this problem. I will describe one of them.
First, let's try to solve a slightly easier version where something like $$$\lceil \log_{1.1} n\rceil$$$ queries are allowed and subset queries are allowed instead of range queries.
The main idea is to maintain a search space of size $$$S$$$ and reduce it to a search space of size $$$\big\lceil \frac{2S}{3}\big\rceil$$$ using atmost $$$4$$$ queries. At the end, there will be exactly $$$2$$$ elements remaining in the search space which can be guessed. The number of queries required to reduce a search space of size $$$n$$$ to a search space of size $$$2$$$ using the above strategy will be equal to $$$4\cdot\log_{\frac{3}{2}}\frac{n}{2}$$$ $$$= \frac{\ln\frac{n}{2}}{0.25\ln 1.5}$$$ $$$= \frac{\ln n - \ln 2}{\ln 1.1067}$$$ $$$< \frac{\ln n - \ln 2}{\ln 1.1}$$$ $$$= \log_{1.1} n - 9.01$$$ $$$< \lceil\log_{1.1} n\rceil$$$.
Given below is one of the strategies how this can be achieved. Let the current search space be $$$T$$$. Divide $$$T$$$ into $$$3$$$ disjoint exhaustive subsets $$$T_1$$$, $$$T_2$$$ and $$$T_3$$$ of nearly equal size. Then follow the decision tree given below to discard one of the three subsets using at most $$$4$$$ queries.

It can seen that all the leaf nodes discard at least one-third of the search space based on the previous three queries.
Now, coming back to the problem where only ranges are allowed to be queried. This can be easily solved by choosing $$$T_1$$$, $$$T_2$$$ and $$$T_3$$$ in such a way that all elements of $$$T_1$$$ are less than all elements of $$$T_2$$$ and all elements of $$$T_2$$$ are less than all elements of $$$T_3$$$. Then all queries used in the above decision tree can be reduced to range queries since it really doesn't matter what are the actual elements of $$$T_1$$$, $$$T_2$$$ and $$$T_3$$$.
Finally, there is just one small optimization left to be done. Notice that when $$$T_2$$$ gets eliminated, only $$$3$$$ queries are used and when $$$T_1$$$ and $$$T_3$$$ get eliminated, $$$4$$$ queries are used. So, it must be more optimal to keep the size of $$$T_2$$$ smaller than $$$T_1$$$ and $$$T_3$$$ but by how much? The answer is given by the equation $$$(1-x)^3 = (2x)^4$$$. It has two imaginary and two real roots out of which only one is positive $$$x=0.35843$$$. So by taking the size of the segments approximately $$$36\%$$$, $$$28\%$$$ and $$$36\%$$$, you can do it in lesser number of queries which is less than $$$\max(\lceil\log_{\sqrt[4]{0.64^{-1}}} n\rceil, \lceil\log_{\sqrt[3]{0.72^{-1}}} n\rceil)-\log_{1.116} 2$$$ which is less than $$$\lceil\log_{1.116} n\rceil-1$$$.
During testing, the testers were able to come up with harder versions requiring lesser number of queries. Specifically, try to solve the problem under the following constraints assuming $$$n\leq 10^5$$$:
#include <bits/stdc++.h>
using namespace std;
void assemble(vector<int> &x,vector<int> &x1,vector<int> &x2,vector<int> &x3,string mask)
{
x.clear();
if(mask[0]=='1')
{
for(int i=0;i<x1.size();i++)
x.push_back(x1[i]);
}
if(mask[1]=='1')
{
for(int i=0;i<x2.size();i++)
x.push_back(x2[i]);
}
if(mask[2]=='1')
{
for(int i=0;i<x3.size();i++)
x.push_back(x3[i]);
}
}
bool query(vector<int> &x1,vector<int> &x2,vector<int> &x3,string mask)
{
vector<int> x;
assemble(x,x1,x2,x3,mask);
int l=x[0],r=x.back();
cout << "? " << l << " " << r << endl;
int y;
cin >> y;
return (y==r-l);
}
void guess(int x)
{
cout << "! " << x << endl;
int y;
cin >> y;
}
void finish()
{
cout << "#" << endl;
}
int main()
{
int tc;
cin >> tc;
while(tc--)
{
int n;
cin >> n;
vector<int> x;
for(int i=1;i<=n;i++)
x.push_back(i);
while(x.size()>2)
{
int m = x.size();
int k = round(0.36*m);
vector<int> x1,x2,x3;
for(int i=0;i<k;i++)
x1.push_back(x[i]);
for(int i=k;i<m-k;i++)
x2.push_back(x[i]);
for(int i=m-k;i<m;i++)
x3.push_back(x[i]);
if(query(x1,x2,x3,"110"))
{
if(query(x1,x2,x3,"100"))
{
if(query(x1,x2,x3,"111"))
{
assemble(x,x1,x2,x3,"011");
}
else
{
assemble(x,x1,x2,x3,"110");
}
}
else
{
if(query(x1,x2,x3,"110"))
{
assemble(x,x1,x2,x3,"101");
}
else
{
if(query(x1,x2,x3,"111"))
{
assemble(x,x1,x2,x3,"110");
}
else
{
assemble(x,x1,x2,x3,"011");
}
}
}
}
else
{
if(query(x1,x2,x3,"100"))
{
if(query(x1,x2,x3,"110"))
{
if(query(x1,x2,x3,"111"))
{
assemble(x,x1,x2,x3,"011");
}
else
{
assemble(x,x1,x2,x3,"110");
}
}
else
{
assemble(x,x1,x2,x3,"101");
}
}
else
{
if(query(x1,x2,x3,"111"))
{
assemble(x,x1,x2,x3,"110");
}
else
{
assemble(x,x1,x2,x3,"011");
}
}
}
}
guess(x[0]);
guess(x[1]);
finish();
}
}










I guess people don't like to see what I wrote, and unfortunately I can't delete the comment (no option to do so), Treat this as a DELETED COMMENT.
I don't really get why I was being downvoted initially (and even now)
I am genuinely interested in knowing that, if someone can politely point out the reason. It will be much appreciated. (will take care about it next time I say something, feel free to see previous revisions).
what was your comment?
You can press the <-Rev. 6
button to see the previous revisions (i.e. what my comment was).
Thank you for your time.
now i wonder too what made you have so many downvotes
C was tough!!
It seems interesting, it's quite easy when find this greedy way in A but harder in C.
I resent working solution on C an hour after AC attempt. Ask questions.
JaySharma1048576 dario2994 kevinsogo Are code or explanations available for the 1F bonus tasks?
The moment, when the greats despaired
I can only provide their codes here because I don't fully understand them
(My rating doesn’t allow me to understand it).dario2994's solution is roughly what I expected (split into up to 8 equal segments, then reduce to two segments).
Not sure what kevinsogo is doing for $$$N>4$$$ though — would appreciate a proof regarding the total number of queries if there is one. It's also not clear to me why the find function never asserts false.
It seems you have pinpointed the most crucial part of my code :)
When I derived this algorithm, I had no proof that
findwould work, just empirical evidence that I tried it for many random tests and couldn't find a breaking case. (And I guess I proved it for small $$$n$$$ just by checking.) But now after you asked, I spent some more effort proving it, and I think I have come up with something that might work.Roughly, it seems to me that we need to show some sort of variation of the Borsuk-Ulam theorem.
Let's make the array circular, and consider its half-open subarrays $$$[i, j)$$$, with appropriate wraparounds, i.e., $$$i$$$ is to be understood mod $$$n$$$, and $$$0 \le j - i \le n$$$. Note that the complement of $$$[i, j)$$$ is $$$[j, i + n)$$$.
Then I defined a cost function $$$f$$$ from subarrays to 2D vectors satisfying the following:
And the goal is to show that $$$f$$$ has a near-zero, i.e., some $$$[i, j)$$$ such that $$$|f(i, j)|_{\infty} \le 1$$$. (In my code, you can see the definition of $$$f$$$ in the comments: its two coordinates are
scostandbcost.)We can think about a continuous version of this, where the indices $$$i$$$ and $$$j$$$ are now allowed to have fractional values, and extend $$$f$$$ into a continuous function in a somehow "tame" way. The claim is that this extended $$$f$$$ has a zero. If this is true, then I'd think that the original, discrete version of $$$f$$$ must also have a near-zero nearby (...maybe, haha; alternatively, maybe the proof of the continuous version can be adapted to the discrete one) which is what we want.
Thus, we seem to need to know the topology of "subarrays of a circular array". Well, I think it's a sphere! Map the subarray $$$[i, j)$$$ to the point on the sphere with longitude $$$\frac{j+i}{n}\pi$$$ and latitude $$$\left(\frac{1}{2} - \frac{j-i}{n}\right)\pi$$$. Then we can check that:
So Borsuk-Ulam applies, and (the extended) $$$f$$$ has a zero.
Now, for a proof of the number of queries, we have two quantities at every step:
Here, we only consider "alive" indices, i.e., those that may still contain the target value. Initially, $$$S$$$ and $$$B$$$ are $$$\approx n/2$$$.
Then, assuming that we are always able to perform a query on a subarray such that:
then we have the recurrences $$$S_{\text{new}} \approx B/2$$$ and $$$B_{\text{new}} \approx (S + B)/2$$$. (This is what the
findfunction accomplishes; it looks for a subarray that will do this.)This then means that the sum $$$S + B$$$ decays with a factor of roughly $$$\phi/2 = 0.8090...$$$ at each step.
Can anyone accurately explain what is asked in Div2 D? I am not getting what probabilities do here since it is about summing values. Also at the start of each excursion are we summing all f or just the pair involved in that excursion?
Expectation is one of the core application of probability.
You could sum up all the values time their probabilities respectively to get the expectation value.
They asked us to sum up the pairs involved in the excursion. The question is so poorly worded that I had the same doubt during the contest.
I don't get it either. I get 7/9 but how does it relate to 777777784?
They want you to kind of find exact values of p and q in p/q. There might be a possibility that you simulate the process and find average according to it or something (then you get the approximate answer by remaining well within the constraints or something). They don't want that, they want you to use math to find the expected value and not implement the selection process in it's entirety.
Yeah, so what should I output? It says calculate p/q mod (1e9+7) but p/q is a fraction, and according to my knowledge the modulo operation is only valid between two integer operands. Btw based username :)
You are to output modulo of $$$p$$$ times Modular inverse of $$$q$$$.
Thanks, I'm new here. I thought -1 was an exponent.
It kind of is, if p/q were an integer less than 1e9+7, It will be equivalent to p/q.
.
div2D another solution.
let X be the sum over all friendship values and N be the number of pairs (which is n * (n — 1) / 2). now consider taking random pair of people from 1 to k. what is the expected friendship value at iteration 1? obviously, it is X / N. what happens then? with probability p = m / N we will take a pair of friends, so we should add +1 to our X, with probability 1 — p we will take a pair of people who aren't friends, so we add +0 to our X. it means that we should increase our X by p * 1 + (1 — p) * 0 = p and continue iteration.
you can check my submission here: https://codeforces.com/contest/1925/submission/243687166
Much concise and clearer than the tutorial, thank you for your explanation!
Concise and efficient!
great solution
I am suffering trying to visualize how x+p actually does it,more like how is probability theory actually works in such case to make sense. May you suggest any tips/clues to help? Thanks.
Thank you for the great explanation!
Can anyone explain the intuition for the GCD properties given in problem B. I got the idea by realizing that for a number k that divides x, you can divide the Ks x/k times over the n spots. Therefore, the answer is the maximum divisor k such that x/k>=n.
It took me a while to see it too. But I guess if you have a,a,a,a,a...a,(x-(num)*a), we want the last term to be a multiple of a. Then you can kind of see that a has to be a factor of k
You can think like this: You want to split $$$x$$$ into $$$a_1,a_2,...,a_n$$$ so as to maximise $$$gcd(a_1,a_2,..,a_n)$$$ subject to the constraints that $$$\sum_{i=1}^{n} a_i = x$$$ and $$$a_i \ge 1$$$ $$$\forall i$$$.
Let $$$gcd(a_1,a_2,...,a_n) = g$$$, then $$$g \cdot (k_1+k_2+...k_n) = x$$$. Hence $$$g$$$ must divide $$$x$$$. So, you can basically iterate over all factors of $$$x$$$ in $$$O(\sqrt{x})$$$ time complexity, and take $$$max(ans,factor)$$$ if $$$x/factor \ge n$$$, as each $$$k_i \ge 1$$$, so $$$\sum_{i=1}^n k_i \ge n$$$. Where, $$$k_i$$$ is just the residual when $$$a_i$$$ is divided by $$$g$$$.
Here's my submission for reference :)
what is k in your solution , k1+k2...kn , i didn't understand that
Oops, I missed it in my explanation:
So, if $$$g$$$ is $$$gcd$$$ of $$$a_1,a_2,...,a_n$$$, that means $$$a_i = g \cdot k_i \forall i$$$ (definition of a divisor). Also, since $$$a_i \ge 1$$$, this gives us the condition $$$k_i \ge 1$$$. I hope, it is clear now :)
You can ask if you have any other doubts.
Thanks ,clear now :)
As the solution of D1C is currently missing, I'd like to explain my solution:
Consider the paper lying flat on a table. The paper has two sides, gray and orange (according to the picture), with gray being originally on top. On every move, the crease lines we make are valleys, but for all layers with orange on top, these valleys actually become mountains once unfolded (since gray ends up on top).
After the first fold, at every point in time and at every point in the paper, there are an equal number of gray and orange layers on top of each other. This is because after the first fold, exactly half of the single gray layer was folded to orange and now there is one layer of both. After every subsequent fold, the balance will stay as all layers are treated equally.
Since an equal length of crease lines is created on each layer of the paper, this means that every round of folds after the first one creates an equal total length of new valleys and mountains. The length of valleys created in the first round of folds is $$$4\cdot\frac{1}{\sqrt{2}} = 2\sqrt{2}$$$. Thus, $$$V = M + 2\sqrt{2}$$$ always holds.
What is the total length of crease lines created on iteration $$$k$$$? Each crease line is $$$\frac{1}{\sqrt{2}}$$$ times the length of a crease line on the previous iteration, but the number of layers of paper doubled. Thus, the total length of created crease lines is multiplied by $$$\frac{1}{\sqrt{2}}\cdot2=\sqrt{2}$$$ every iteration. Thus, on iteration $$$2$$$, the total length of added crease lines is $$$\sqrt{2}\cdot2\sqrt{2} = 4$$$. Exactly half of this, i.e. $$$2$$$, is the total length of added mountains (and also the length of added valleys).
On each subsequent round, we add $$$\sqrt{2}$$$ times more mountains than the previous round. Let $$$x = \sqrt{2}$$$. Now, for fixed $$$N$$$, we have $$$M = 2 + 2x + 2x^2 + 2x^3 +\dots+ 2x^{N-2}$$$ and $$$V = 2 + 2x + 2x^2 + 2x^3 +\dots+ 2x^{N-2} + 2\sqrt{2}$$$.
The remaining part of the solution is boring: We can notice that the value of $$$M$$$ is a geometric sum, we can calculate its value with the formula $$$\displaystyle\frac{a(1-q^n)}{1-q}$$$, where $$$a$$$ is the first term, $$$q$$$ is the ratio between consecutive terms and $$$n$$$ is the number of terms. This also solves $$$V$$$ as $$$V = M + 2\sqrt{2}$$$. We need to represent the values of $$$M$$$, $$$V$$$ and finally $$$\frac{M}{V}$$$ in a form like $$$a+b\sqrt{2}$$$ with $$$a, b \in \mathbb{Q}$$$. To do this, we will have to get rid of square roots in denominators. This can get tedious, so the formula $$$\displaystyle\frac{a+b\sqrt{2}}{c+d\sqrt{2}} = \frac{ac-2bd}{c^2-2d^2}+\frac{bc-ad}{c^2-2d^2}\sqrt{2}$$$ can be very helpful. Exact details are left as an excercise to the reader. Splitting even and odd $$$N$$$ will be useful.
$$$\displaystyle\frac{a+b\sqrt{2}}{c+d\sqrt{2}} = \frac{(a+b\sqrt{2})(c-d\sqrt{2})}{(c+d\sqrt{2})(c-d\sqrt{2})}$$$ (as long as $$$c\ne0\vee d\ne0$$$, since $$$c, d\in \mathbb{Q}$$$).
$$$= \displaystyle\frac{ac+b\sqrt{2}c-ad\sqrt{2}-b\sqrt{2}d\sqrt{2}}{c^2-(d\sqrt{2})^2}$$$
$$$= \displaystyle\frac{ac-2bd+bc\sqrt{2}-ad\sqrt{2}}{c^2-2d^2}$$$
$$$= \displaystyle\frac{(ac-2bd)+(bc-ad)\sqrt{2}}{c^2-2d^2}$$$
$$$= \displaystyle\frac{ac-2bd}{c^2-2d^2}+\frac{bc-ad}{c^2-2d^2}\sqrt{2}$$$
PS, Why is the mod $$$999\,999\,893$$$? Are there some cases where the answer isn't defined modulo $$$10^9+7$$$ or modulo $$$998\,244\,353$$$?
Very intuitive explanation. I saw the question and thought there must be a numberphile videos on this.
Yeah I did the same. I also wrote a
structto store $$$x+y\sqrt{2}$$$ which was very convenient and easy to debug.$$$999$$$ $$$999$$$ $$$893$$$ is the largest prime number under $$$10^9$$$ under which $$$2$$$ is a quadratic non-residue.
I might be missing something very simple, but why do we want 2 to not be a quadratic residue? Why would the existance of "sqrt 2 under modulo" be a bad thing?
Answer is not defined if sqrt 2 exists (a + b root 2 can be written with other values of b)
But the statement doesn't say "find $$$A$$$, $$$B$$$ for which $$$A+B\sqrt{2}\equiv MV^{-1} \pmod{p}$$$", it says "find $$$A$$$, $$$B$$$ for which $$$A+B\sqrt{2}=\frac{M}{V}$$$". The fractional value of $$$B$$$ is well defined regardless of the modulus used since it is defined by equality, not congruence under modulo. This means that the value of $$$B$$$ under modulo is well defined unless $$$B=\frac{p}{q}$$$, where $$$p, q\in\mathbb{Z}$$$, $$$\gcd(p, q) = 1$$$ and $$$q \equiv 0 \pmod{p}$$$.
If instead, your argument is that "sqrt 2 doesn't exist under modulo $$$\Rightarrow$$$ it is harder to misunderstand the problem", then I think I can agree with that. But I still wouldn't change the modulus to something non-standard for this reason.
Or am I wrong?
You are correct, idk the reason either now
Maybe because $$$c^2 - 2d^2$$$ (the denominator) can be $$$0$$$?
So let's test this theory. If you take the math to its natural end you will find out that the value of $$$y$$$ such that $$$x + y\sqrt{2} = \frac{M}{V}$$$ is exactly, with no modulo reductions:
Where $$$b = 2^{\lceil n/2\rceil} + 1$$$ and $$$a = 2^{\lfloor n/2 \rfloor} - 1$$$. Since $$$b$$$ is always either $$$a + 2$$$ or $$$2a + 3$$$ it's easy to check that no big prime can divide both $$$a$$$ and $$$b$$$, and thus no big prime can divide both the numerator and the denominator either. So we require $$$2b^2 - a^2$$$ to never be divisible by $$$p$$$ for our modulo of choice $$$p$$$. Assuming $$$b$$$ is nonzero modulo $$$p$$$ this gives
So there you have it, as long as $2$ is a quadratic non-residue modulo $$$p$$$ we are guaranteed to be able to compute the answer. Since $$$2$$$ is a quadratic residue for both standard choices $$$p = 10^9 + 7$$$ and $$$p = 998244353$$$, this seems to me like a good enough reason to change the modulo.
However, you might argue that even if $$$2$$$ is a quadratic residue, that doesn't mean that the answer is impossible to compute. After all, $$$a$$$ and $$$b$$$ are something specific and not whatever you want them to be. So let's go a bit further. I'll focus on the case where $$$n$$$ is even and therefore $$$b = a + 2$$$. Then
And so we want
To never happen. We know $8$ is a quadratic residue for the usual primes since $$$2$$$ is, so choosing $$$a \equiv \sqrt{8} - 4 \pmod{p}$$$ for either modular square root of $$$p$$$ fails. But wait! $$$a$$$ is not equal to just any number, it must be equal to $$$2^x - 1$$$ for some $$$x$$$. So in fact we need
Clearly this is much better, there's nooooo way a power of $2$ just happens to give one of these two random values modulo $$$p$$$ for both of our standard primes. Unfortunately it just so happens that for both $$$p = 10^9 + 7$$$ and $$$p = 998244353$$$ the order of $$$2$$$ modulo $$$p$$$ is $$$(p - 1)/2$$$, and so $$$2^x \pmod{p}$$$ passes through every single quadratic residue modulo $$$p$$$.
But there's still some hope! There's no reason both values of $$$\sqrt{8} - 3$$$ have to be quadratic residues... Aaaand it's dead, for $$$p = 998244353$$$ and $$$\sqrt{8} = 232390342$$$ we have that $$$\sqrt{8} - 3$$$ is a quadratic residue. But wait! Both of the choices actually turn out to give quadratic non-residues modulo $$$10^9 + 7$$$! Surely these silly authors should have just gone with that instead of their weird modulo...
Nope, recall that $$$b = a + 1$$$ is only one of the possibilities, we also need to discard $$$b = 2a + 3$$$. Doing similar math we find that the bad case here is
Significantly less clean than the previous case, but equally solvable. We now need to check the square roots of $2$ modulo $$$p = 10^9 + 7$$$ and see if the resulting expression is a quadratic residue. For $$$\sqrt{2} = 59713600$$$ this turns out to be a non-QR, and for $$$\sqrt{2} = 940286407$$$... wow! also a non-QR! Very unexpected!
So in summary, while $$$p = 998244353$$$ is a no-go, it turns out that the authors could have safely chosen $$$p = 10^9 + 7$$$ and kept the answer computable. My question for you now is, if you were the author, would you rather go with the non-standard modulo that clearly works, or the standard modulo that basically only works because we won four coin flips in a row and could have easily sent contestants with more number theory experience on a wild goose chase like the one I just sent you on?
Now that I understand the reasoning behind it, I would definitely choose the non-standard modulo.
Your comment seems a little passive aggressive, possibly because of my comments about "this is not a good enough reason to change the modulo", and I don't really like that. I wasn't trying to critisize the problemsetters' choices of modulo; I was just looking for a good explanation for that, and your comment managed to do that. Before your explanation, I didn't know why having 2 be a quadratic non-residue was desirable — now I know.
Anyway, thanks for the explanation!
Sorry if it came off that way, it's definitely a good and valid question and I was mostly trying to emphasize that one of the standard modulos working seems very unlikely at a glance.
Someone pls help me with my submission for C div 2 ... pls help me with the test case being failed ..
i am just checking for every character till kth place , ahead of its first index there must be present at least n-1 characters of each type for an answer..
243690556
If you are just checking for n-1 occurences of each character ahead it might fail for abcaaabbbccc , n=4 , k=3 a,b,c, all have n-1 occurences ahead of them, but the string can't make all subsequences. I have not checked your code, but this might be the problem in your approach
oh,Your approach is the same as mine during the contest, both wanting to use this method to check if there are n abcs This kind of arrangement string. However, this idea is problematic
For example, aaabbbcccaaabbb
You will find that there is no substring like CBA, but the result obtained using the above approach will be YES.
So the correct way should be to use greed to check.like this
I think I might used a similar approach and just came to know what was the problem with this approach. if I understand correctly you are checking that if the freq of the character you have right now is let's say x then every character must be present n-x times in its suffix, but the problem is that we are not considering the order of the characters in this approach, that's why this will give the wrong answer.
?
Hi for D cant we just directly put the values and answer in O(1).
Using pnc we get expected value = [((k*f)*(nC2) + (k*(k-1))*m/2]/(nc2)^2 ?
I was getting wrong answer for test case 6. I think the limits just go boom. Can someone check the code and point where is the thing going wrong?
Do all the math in this problem with long long instead of int. Otherwise you WILL have overflow in the multiplications.
Ah i defined int as long long. I didn't take mod for f sum so it overflowed
244468721[submission:244468721]
I have a dp solution for 2C/1A.
Let dp[i][c] be the largest n such that any string of length n ending with c is a subsequence of s[1…i].
We have two relations
dp[i][c] = dp[i-1][c] for c != s[i]
dp[i][s[i]] = max(dp[i-1][s[i]], min(dp[i-1][c]) + 1); c = a, b, …
Now we know the answer is “NO” if and only if there exist c such that dp[m][c] < n. Choose that c as the last character in our answer, and continue doing this again. Now we can construct the solution from the back, then reverse it to get the answer.
I also came up with same idea but got stuck at printing the non occuring subsequence . But finally again tried an hour ago and solved it.
Can anyone explain the formula in Div2D?The tutorial is like not writing it.
Expectations can be tough to think about. Here is a mathematical proof for Div2D [Note that it requires basic understanding of probabilities and expectations]:
Let pair 1 occur $$$X_1$$$ times, pair 2 occur $$$X_2$$$ times $$$\dots$$$ pair $$$m$$$ occur $$$X_m$$$ times in the $$$k$$$ excursions. Let $$$F(X_i, i)$$$ be the total contribution of $$$i-th$$$ pair to the total friendship. Hence, if total friendship is $$$F_{tot}$$$
$$$F_{tot} = F(X_1 , 1) + F(X_2 , 2) + \dots + F(X_m, m)$$$ subject to $$$X_1 + X_2 + \dots + X_m = k$$$. Here, each $$$X_i$$$ is a random variable which takes value in the range $$$[0,..,k]$$$.
Clearly, $$$E[F_{tot}] = E[F(X_1,1)] + E[F(X_2,2)] + \dots + E[F(X_m, m)]$$$ using linearity of expectation [even though $$$X_i$$$'s are contrained]. This is the power of linearity of expectation.
What is $$$E[F(X_i, i)]$$$ ?
If $$$i-th$$$ pair occurs $$$x$$$ times in the excursion. So, the contribution is $$$f[i] + (f[i] + 1) + ... + (f[i] + x - 1)$$$. Which can be simplified to $$$ f[i] * x + x * (x - 1) / 2$$$.
It is easy to find $$$E[F(X_i,i)] = \sum_{x=0}^{x=k} F(x, i) P(X_i = x)$$$ = $$$\sum_{x=0}^{x=k} (f[i] * x + x* (x - 1) / 2) * P(X_i = x)$$$.
How to simplify this?
For each $$$f[i]$$$ the answer is just $$$\sum_{x=0}^{x=k} (f[i] * x + x* (x - 1) / 2) * P(X_i = x)$$$ = $$$f[i] * \sum_{x=0}^{x=k} x*P(X_i=x) + \sum_{x=0}^{x=k} x*(x-1)/2 * P(X_i=x)$$$
Note that $$$P(X_i = x) = {k\choose x} * \frac{{(totalPairs-1)}^{k-x}}{totalPairs^k}$$$ .Idea, is that there are $$$k$$$ places. You have to reserve $$$x$$$ places. In each of the $$$x$$$ places, where you place the pair the probability is $$$\frac{1}{totalPairs}$$$ and in the remaining $$$k-x$$$ places where you don't, the probability is $$$\frac{totalPairs-1}{totalPairs}$$$. You can then multiply be $$${k \choose x}$$$. And, also $$$totalPairs$$$ is $$${n \choose 2}$$$.
So, for each $$$f[i]$$$ the answer can be expressed as $$$f[i] * A + B$$$ where $$$A$$$ and $$$B$$$ can be precalculated as they don't depend on $$$i$$$.
This gives the proof behind expression used in the editorial.
Submission: here
Even though I'm not the original OP, Thankyou so much for this!
Div2 is pretty good for me, though why is Div2C reused as Div1A? I think that's a pretty cheap move, you know...
ain't that always how it is for same round but separate division?
Oh wait, I didn't realize this. Tks
my submission Logic I am trying to make blocks which have k smallest character greedily.
It's failing on test case 2, can anyone tell me what's wrong with my logic, code is self explanatory
bro this part is wrong you should add last character of the block but you adding the first character from block which has count 1,let for k=3 block is "abbc" you should add 'c' but you adding 'a'. replace above two lines with
Thank you, but adding s[i] means that this character will definitely have a frequency of 1, but I am adding the character that also have a frequency of one,so how does it affect the final answer.This part is not clear by me. Can you please explain this, or just give me counter test case it would be much helpful.
Let n=2 , k=3 , s="abbcab" In this 1st block will be "abbc" and 2nd block which is incomplete will be "ab" In 1st block you adding 'a' instead of 'c' , because 'a' also have count 1 and find function returns iterator of first matched element. Your logic giving ans "ac" but it is present and ans should be "cc".
Thank you so much!
In div2B "The maximum GCD that can be achieved is always a divisor of x" . Can anyone please explain why is that? I'm not getting this point.
gcd(a1,a2,a3...an)=gcd(a1,a1+a2,a1+a2+a3,...,a1+a2+a3..+an) so at the end we get sums of all sub problems which is just x so answer is gcd(a1,a1+a2,....,x) so ans is always divisor of x .
Consider an array of numbers $$$a_{1}, a_2, ..., a_n$$$.
Let $$$g$$$ be the greatest common divisor (gcd) of all these numbers.
Since every number is a multiple of $$$g$$$, we can express each number as follows:
$$$a_1 = g * k_1$$$
$$$a_2 = g * k_2$$$
...
$$$a_n = g * k_n$$$
where $$$k_1, k_2, ..., k_n$$$ are positive integers.
The sum of these numbers is:
$$$a_1 + a_2 + ... + a_n = g * (k_1 + k_2 + ... + k_n) = x$$$
Therefore, $$$g$$$ should be a factor of $$$x$$$.
And here all $$$k_i$$$'s are positive integers so $$$\sum k_i \geq n$$$ hence we have to find smallest factor of $$$x$$$ that is greater that or equal to $$$n$$$ ,say $$$f$$$
Then $$$x/f$$$ is our required $$$g$$$
Why div2 D must take the probability modulus, and can not be expressed as a decimal like normal problems, and give a precision requirement?
Why so many math problems
It's a math website
For 1D,I have a easier solution.243652894
By the way; it is 2D. Can you please explain your solution?
We can treat each pair of friends separately. Regardless of the pair of friends, the probability of selecting them is $$$p=\frac{1}{\frac{n(n-1)}{2}}$$$.
At the jth excursion, if the ith pair of friends is selected, then its contribution to the answer is $$$f_i+q_i$$$, where $$$q_i$$$ is the expected value of having selected the ith pair of friends earlier, and we get $$$q_i=p\times(j - 1)$$$. Then if we are not sure if the ith pair of friends was selected (the probability of selection is $$$p$$$), the contribution of the ith pair of friends to the answer in the jth tour is $$$p(f_i+p\times(j - 1))=pf_i+p^2(j - 1)$$$.
Combining the contributions to the answer from the i-th pair of friends in the kth excursion, the
After the contribution of the ith pair of friends to the answer has been counted, the answer is obtained by adding up the contributions of each pair of friends to the answer.
This is the result.The time complexity is $O(t\log MOD + m)$.
Look here.It's my new solution.243708880
In Problem "2D. Good Trip" Tutorial,
Shouldn't it be "x Choose k" inplace of "k Choose x"?
Can someone help me in finding what did i do wrong in 2C
243641202
i was trying to make the ith letter x by checking is every combination of previous letters is possible or not
Take a look at Ticket 17324 from CF Stress for a counter example.
thanks!
For Div2D, each excursion increases the expected friendship value of every (non-zero) friendship pair by $$$\dfrac{1}{p}$$$, where $$$p$$$ = $$$\dfrac{n(n-1)}{2}$$$. So the expected friendship value of the $$$i$$$-th pair after $$$j$$$ excursions is $$$f_i + \dfrac{j}{p}$$$. So the expected friendship value of the pair picked after $$$j$$$ excursions (i.e. for the $$$(j+1)$$$-th excursion) is $$$\sum\limits_{i=1}^{m}\dfrac{1}{p}{(f_i + \dfrac{j}{p}})$$$.
Using this, we can come up with a straight-forward formula for the answer:
Which simplifies to:
Code : 243709626
For C I created a dynamic programming solution : Can someone verify as I am getting TLE on test 3..
dp[i][L] = 1 (if we can make all possible strings of length L using characters 'starting' from index i) else 0 Now we can loop over every character find the smallest index greater than i where it occurs using a character-set map . Say,the smallest index greater than i is ind, (if it doesnt occur we can make dp[i][L] =0) . So, if dp[ind+1][L-1] is true that means we can make all strings possible starting with the character I am currently checking.
As the time complexity is 26*26*O(m) , it wont pass however I was interested in its correctness.
243709963
İf you still interested in the solution you can see my submission list I made the same mistake if you need any help you can ask me
Why does the submission for 2C TLE? 243710719 Isn't the time complexity $$$O({m^2}n + mnk)$$$ which should pass within the time limit?
The sum of m over all test cases is mentioned to have an upper bound of 10^6 so it wont pass
Problem B
Can someone kindly explain why the condition for the loop is i*i<=x?
we want to check divisors $$$\le \sqrt{x}$$$. for each divisor $$$d \le \sqrt{x}$$$, we also check $$$x / d$$$, because it will be another divisor of $$$x$$$, and we don't need to check any divisor $$$\gt \sqrt{x}$$$, all of them were already checked.
To Reduce TC:
if i is a factor then x/i is also a factor, similarly for sqrt(x).We need to loop till sqrt(x) because all factors after it had already been taken [ by (x/i)]
i thought in div2c we have to print string which contains all the subsequence which is not present in original string
Can some please explain why the following solution doesn't work for problem C
Observation in div2. D: all the sums of expected values of every friendship increases in a pattern: if n = 3, m = 1 and there is a bond of 1 between 1 and 2, in the first turn the expected value is 1 * 1/3 = 3/9. In the second turn, 2 * 1/9 (increased) + 1 * 2/9 (still) = 4/9. On the next turns it goes like 5/9, 6/9 and so on. The contribution of every bond can be calculated in O(1).
Solution for Div-2 C is giving wrong answer in test case: 1 4 3 12 abcaccabcabc
Output: NO aaaa
As it is clearly visible 'aaaa' is a possible subsequence
Output is
NO cbba243618528 can someone point out as to why this is failing on pretest 2? My thought process was that since we need atleast n occurences of a character in a string to count that , also there could be a case where a character may not be present in the string at all. So i found which characters among the first k were present.
Take a look at Ticket 17323 from CF Stress for a counter example.
cool thanks!
There should be at least one testcase in the pretest which can cause TLE or a large testcase should be added on the pretest. I got passed in the pretest section of B simply on the first attempt and didn't came with another try for optimized solution, which caused tle on the system testing.
problem B is a subproblem of problem 803C - Maximal GCD.
E's solution k got declared as int while the bound is <= 1e12. Even in the test case there is some test with k >= 1e10. I submitted the code and it actually worked ?
Oh sorry didn't see your #define there
Hi, I don't know if it's legitimate to ask for this but yesterday I got a tle on the div2 E 243653603
However, submitting the exact same code in C++ 64bits makes it ac (in 1sec). 243744788
Please, would it be possible to get a rejudge ? Also if anyone knows why C++ 64 bits is that much faster, I'll gladly take it (the last time I used C++ 64 bits, I got tle because of it...).
Thanks by advance for the help
JaySharma1048576
Iirc when you're doing many operations with 64-bit integers, 64-bit compilers are significantly faster. I believe 64-bit compilers are faster (or at least not slower) most of the time. Where did you get tle with 64-bits and ac with 32-bits?
Also, this has happened to quite a few people before and I don't think anyone has gotten a rejudge, so you're probably out of luck.
Thanks for your answer, it sounds like a reasonable explanation.
In this problem 1250B - The Feast and the Bus I got tle in C++ 64 (243748301) and ac in C++ 17 (243748727). I also have a friend who got tle for similar reasons on a shortest path problem I think ? I'll try to find it but it was a long time ago
By the way, if the runtime can change that much, during the testing phase, can't they try to submit solutions in both C++ 64 bits and 32 bits to avoid such things happening ?
Here is your code with removing
#define int long longand chaning oneinttollhttps://codeforces.com/contest/1925/submission/243752795Gets an AC with C++ 17, not very strong though (because there are still a lot of lls)
Oh thanks ! I wouldn't have thought that changing only a few ints to long long would make such a difference as most of the operations are in the segtree
What is wrong with my logic for div 2D?
Each of the $$$m$$$ pairs of friends has a probability of being chosen $$$\frac{2k}{n(n-1)}$$$ times over the $$$k$$$ excursions. Then, the expected value can be calculated by summing $$$\frac{(2f_i+(\frac{2k}{n(n-1)}-1))(\frac{2k}{n(n-1)})}{2}$$$ for all $$$1 \le i \le m$$$. (This is by using sum of arithmetic series).
You are looking for the probability of a pair being chosen a fixed number of times (probability that the pair gets selected i times).
What you are doing is just like, wrong
I would recommend you to learn a bit about expected value (definition, linearity) and to do things more formally. You want E(S) where S is the sum of friendship values of all k pairs chosen for the excursions.
S = X1 + ... + Xm where Xm is the sum of friendship values of pair i (over all the excursions it was chosen for).
By linearity: E(S) = E(X1) + ... + E(Xm)
Now, to compute E(Xi) you can fix how many times the pair i has been chosen and you end up with a simple sum to compute (which is a bit similar to what you sent, except you need some binomial coefficients for the probabiltiy).
First of all, thank you for the reply. Sorry, but I don't understand what you mean by "fix how many times the pair i has been chosen". Could you provide an example of calculating $$$E(X_i)$$$ using "binomial coefficients for the probability"?
Thank you very much.
So let's consider pair i.
$$$E(X_i) = \displaystyle\sum_{j = 0}^{k} {val(j) \cdot P(X_i = j)}$$$ (I technically skipped a step here, but overall it's just partitioning the events depending on how many times the pair i was chosen).
And $$$val(j) = f_i + ... + (f_i + j - 1)$$$ (which has a closed form that you pointed out in your original comment)
Now, you are looking for $$$P(X_i = j)$$$ which actually follows a binomial law.
If you don't know what that is, I'll just try to explain intuitively: - you have probability $$$p = \frac{1}{\frac{n \cdot (n - 1)}{2}}$$$ for the pair i to be chosen at a fixed excursion
so if you fix the $$$j$$$ excursions at which the pair i is chosen, the probability to be chosen exactly at these excursions is $$$p^{j} \cdot (1 - p)^{k - j}$$$
you have $$$\binom{k}{j}$$$ ways to chose the $$$j$$$ excursions at which the pair will be chosen
So overall, $$$P(X_i = j) = p^{j} \cdot (1 - p)^{k - j} \cdot \binom{k}{j}$$$
can u explain div1 B ?
Problem D can also be solved in $$$O(m)$$$. See here.
2 line Solution for Div 2D
...
C is really hard for me. Frustrated : (
2D has a direct formula.
Let $$$d=\frac{n\left(n-1\right)}2$$$, which denotes the number of pairs of children, and $$$s=\sum_{i=1}^mf_i$$$, which denotes the sum of friendship among each pair of friends in the beginning.
In each round, the probability of choosing a pair who are friends is $$$p=\frac md$$$.
Then, after $$$i$$$ rounds, the expected value of increase is $$$ip$$$, so the expected value of sum of friendship among each pair of friends is $$$s+ip$$$. Then, the expected value of friendship of the chosen pair in the $$$i$$$-th round is $$$\frac{s+ip}d$$$.
Therefore, the answer will be $$$\sum_{i=0}^{k-1}\frac{s+ip}d=\frac{ks}d+\frac{mk\left(k-1\right)}{2d^2}$$$. It can be calculated using constant time.
Great solution. I didn't notice that sum of $$$k$$$ is bounded in the problem statement. So although I came up with an $$$O(m+k\log p)$$$ ($$$p$$$ is the modulo) solution, I didn't think it could pass and did not submit. So I tried to transform my original formula (which is similar to the expectation of a binomial distribution) into a direct formula through an algebraic way during the whole contest. Of course I failed. Now I realize that I should use an alternative explanation to form another simpler formula instead of transforming the original formula directly.
I have just done D to upsolve, should have read that in contest. I recently solved a problem 1761F1 - Anti-median (Easy Version) and used this as a subproblem to get sequences in which there will definitely exists a k regular bracket as subsequence. :(
Anyone using sqrt decomposition to solve div2 problem E? I divide the sequence into $$$\lceil\sqrt n\rceil$$$ blocks, with each block at most $$$\lceil\sqrt n\rceil$$$ length (the last block is cutoff to a lower size). Then for each insertion of harbour, I find its left harbour $$$l$$$ and right harbour $$$r$$$ and then update the blocks in $$$[l,r]$$$; for each query $$$[l,r]$$$, I also retrieve the information in blocks in $$$[l,r]$$$. I think it should cost $$$O(q\sqrt n)$$$ and should get passed. However I got time limit exceeded: https://codeforces.com/contest/1925/submission/243770890. Could anyone help?
$$$\Theta\left(q\sqrt n\right)$$$ is too large for this problem because $$$q\sqrt n=164316767.25154984$$$ and the constant is not small enough.
It is much better to process a problem with interval assignments and interval queries using a segment tree which has time complexity $$$\Theta\left(n+q\log n\right)$$$ than a block array which has time complexity $$$\Theta\left(n+q\sqrt n\right)$$$.
Thanks!
My AC square root decomposition code: 244297448
Well I further optimize my code. I found my previous complexity if actually $$$O(q\sqrt n\log n)$$$. Now I optimize it to $$$O(q\sqrt n)$$$ but is still TLE: https://codeforces.com/contest/1925/submission/244358049. I think it may need some specific tricks to get passed with such a complexity.
Interesting. I tried several times submissions with different compilers and got accepted: https://codeforces.com/contest/1925/submission/244359152
I have to admit this was a great contest. Unfortunately in Div 2 B i forgot to check sqrt(n) and only checked everything else , noticing this costed me 40 minutes but im glad i solved it anyway.
Can anyone please explain div2E?
Thanks in advance.
Idea of my solution: (243815910)
We can compute the initial answer by a sweep from 0 to N — 1 maintaining the current nearest left and nearest right harbour as iterators in the initial set. There might be easier ways but at least this doesn't need range update. Sorry that it's sideways. Maybe you can download and rotate it.
thanks bro
Can anyone give a counterexample or explanation why this solution doesn't work? https://codeforces.com/contest/1925/submission/243789503
Nice explanation
Can somebody please provide an inductive proof for Case 2 of 1D?
Problem E: My submission (WA on test 8)
My approach:
▶ Calculate the initial cost for each N ship and build a segment tree on it.
▶ Say a new harbour is built at position $$$z$$$ and value $$$v$$$. Say The nearest left neighbour is $$$(x, v_1)$$$ and the nearest right neighbour is $$$(y, v_2)$$$. Then the cost of ships in the segment $$$(x + 1, z)$$$ is decremented by $$$(v_1 * (y - z))$$$, and the cost of ships in the segment $$$(z + 1, y - 1)$$$ gets multiplied by $$$(v / v_1)$$$.
▶ I used lazy propagation for range multiplication/division and addition.
Can someone point out the mistake?
Take a look at Ticket 17298 from CF Stress for a counter example.
Thanks. Why is this one failing?
Take a look at Ticket 17306 from CF Stress for a counter example.
how are differentiating whether addition was performed first or multiplication ?
order matters here right?
I am storing the lazy values $$$(M, A)$$$ for each node of the segment tree, which means that we must multiply the value at that node with $$$M$$$ first and then add $$$A * (r - l + 1)$$$ (r — l + 1 is the length of the segment covered by node) to it, i.e., $$$(val * M + A * (r - l + 1)$$$. Now let's say we are pushing the lazy information of a node, say $$$(M_1, A_1)$$$ to its child with lazy information $$$(M_2, A_2)$$$ then we can observe that $$$(val * M_2 + A_2 * (r - l + 1))$$$ becomes $$$(val * M_1 * M_2 + (A_2 * M_1 + A_1) * (r - l + 1))$$$. Hence, we can accordingly modify the lazy_multiply and the lazy_add values. ( NOTE: The identity for lazy_multiply and lazy_add are 1 and 0 respectively. Since we also need to do the division operation, there is also a lazy_div for each node in actual implementation. )
t[l].lazy_add = (t[l].lazy_add / t[id].lazy_div) * t[id].lazy_mul + t[id].lazy_addYou are rounding values here.
t[l].lazy_addmay not be divisible byt[id].lazy_divObservation: $$$A_i$$$ is always of the form $$$val_i * xyz$$$ and
t[id].lazy_divis always a divisor of $$$val_i$$$ so there will be always an exact division.it works i do it in same way. code
Thank you for letting me know that it's correct.
How did you handle division without a lazy value for division? And why did you take mod? The original problem wasn't asking us to print the answer modulo M.
I guess the problem in your solution is that the lazy division values can overflow if multiple updates are stacked on top of each other without pushing further. tmpzlp's solution uses a big prime modulo larger than the largest possible answer, and this solves all of your problems:
__int128needs to be used for multiplication.Got it. Thank you, sir. Btw, such a cool usage of
__int128^w^Can anyone explain in 2B, why we need the condition n <= i? I'm not knowing what case it works for
We are just walking from 1 to sqrt(x)
When x divides i, that means there are 2 divisors of x, not just one -> i , x / i
The first condition handles the first divisor and the second handles the second
so the factors of x that are greater than sqrt(x) are just the same product we have seen before sqrt(x) but written vice versa?
like if we have seen (a*b) before square root it's the same numbers repeating again but in reverse like b*a?
Exactly.
If it's a new concept for you, you should study number theory.
Sure, will do
How to solve Div2E/Div1B? Still waiting for the editorial :\
My solution:
For each harbor I keep the sum of distances of every ship between this harbor and the next harbor. I can do it using a std::set maintaining the positions of all available harbors. Now i put the mentioned value for a harbor at position x inside a Fenwick tree ( the xth number in the Fenwick tree, if there is a harbor at position x, contains the value of that harbor). Now let's talk about answering each query, in each query i First take the sum of all values of harbors inside that segment. It's really easy to see that there are some ships in the segment that I'm not counting their distance but I should, and there are some ships outside that I'm counting their distance but I shouldn't. I can calculate these missing/extra values using the std::set we maintained above. It is a bit mathy, so I recommend taking a look at my implementation to understand it better: 243623915
Your method doesn't require lazy propagation. Great.
Can you please tell me if this approach will work? (Although it is a bit messy to implement)
Can anyone tell me what's wrong with my code on Problem C. I compared it with the editorial and think they are the same, but I got WA. https://codeforces.com/contest/1925/submission/243847499
Take a look at Ticket 17322 from CF Stress for a counter example.
For the Div2 D, for considering the incremental sum of pairs, why they have assumed that for a excursion only 1 pair can be repeated and they only accounted that pair repeated k x times, and multipled the whole by m? Why can't 2 or more pairs be a part of excursion considering that sum and probabilites would change and the final solution would also, right?
Can someone tell me how to determine the time complexity of div 2 b?? according to the constraints if feels like O(n) solution to work since n<=1e8 but my O(n) solution gives tle?? here is the solution 243588276
You have to consider the number of test cases also
I haven't had any problems like this before and i have never considered the number of test cases before as well, is this because in most problem there is a statement like:- "It is guaranteed that the sum of n and sum m over all test cases does not exceed 1e5 and the sum of k over all test cases does not exceed 2⋅1e5." While this question didn't??
Yep that's exactly the reason
thank you
Please help me in identifying the mistake in my code. Do you have any counter example for this? Getting wrong answer on test case 3639 of test 2. Submission
Take a look at Ticket 17315 from CF Stress for a counter example.
Will we see $$$1B \; 1C\; 1E$$$ solutions?
The editorial for 1C has been added. Unfortunately, there was an Indian ICPC Regionals contest the very next day of this contest and all three of us were judges for that contest. We didn't get any time on Sunday to write the formal tutorials in the editorial and the author of 1B and 1E was busy today. Hence, the delay.
I think there is a little mistake in the constants in d1F editorial.
The equation we should be solving for is $$$(2x)^{\frac{1}{3}} = (1-x)^{\frac{1}{4}}$$$, as we are multiplying the segment size by $$$2x$$$ in the 3-query case and by $$$1-x$$$ in the 4-query case. This yields $$$x \approx 0.35843$$$.
Asymptotically this gets better queries than in the editorial: taking $$$x = 0.35843$$$, $$$y = 0.36801$$$, $$$n = 10^5$$$,
but
Also, using this value of $x$, both sides of the $$$\max$$$ are equal, so it's optimal.
(243955536 -- doesn't work without rounding!)
We may also precompute all optimal choices to guarantee the optimal number of queries ($$$102$$$ when $$$n=10^5$$$): (243955904)
Yeah, you are right. I probably messed up something while writing the editorial. But it was an editorial-only bug. The constraints in the problem are correct and according to the better bounds found by you. You can check that $$$\log_{1.116} 10^5 = 104.8$$$ which is according to the value of $$$x$$$ and not $$$y$$$.
And yeah, the solution works only after rounding. There is a buffer of just $$$1$$$ query between the constraints and the calculated bound so you have to be quite precise.
Actually, surprisingly my solution with the incorrect constant passes the tests when always rounding down (243937391), even though theoretically it should fail. I guess it is hard to kill solutions with slightly suboptimal constants at high values of $$$n$$$, as sometimes you'll get lucky and get 3 queries when the worst-case is 4.
unable to understand why they are doing this in div2B
if(n<=i){ ans=max(ans,x/i); }
edit: nvm for anyone with the same doubt check this explanation https://codeforces.com/blog/entry/125137?#comment-1111266
Problem C's solution was very nice, but may be very difficult to prove. But, it made me wonder if authors prove their "greedy" solutions or not? And this is NOT to criticize the editorial. I was wondering if there have been cases where an author came up with a problem, which had an obvious greedy solution but later came out to be wrong because someone came up with a test-case where it didn't work. Maybe experienced participants can tell.
Otherwise, if every author proves their greedy problem I believe they should post their proofs as well. It will benifit others a lot. Since, greedy is something which doesn't come naturally to everyone and a lot of competetive programmers struggle with it. If something reduces to some standard greedy, then it's okay. But in other cases a proof should always be present in my opinion. That would at least guarantee that someone doesn't hack the author's solution
This probably happens every now and then during the problemsetting process — usually this would be noticed during stress testing. But sometimes shit happens and these mistakes aren't caught, even with stress testing. For example Codeforces Round 846 (Div. 2) had a problem C with an intended greedy solution, but it turned out to be incorrect. The round got unrated and the problem was deleted as it was unsolvable with the given constraints.
Well, I do have a proof for 2C/1A. It is easy and intuitive so I felt it unnecessary to explain in the editorial.
Let the counter-case we are building using the greedy until we reach the end of $$$s$$$ be $$$t$$$ and the final counter-case be $$$c$$$. There are two things that must be proven:
Firstly, notice that the greedy algorithm divides the string $$$s$$$ into some blocks with each block (except possibly the last one) containing all the first $$$k$$$ English alphabets and where the last character appears exactly once in the block in the end.
So, if you are aware of the well-known greedy algorithm to check if a given string $$$a$$$ is a subsequence of another string $$$b$$$ or not, you can notice that the first character of $$$t$$$ must match to the last character of the first block of $$$s$$$ since there is no better choice for it, the second character of $$$t$$$ must match the last character of the second block of $$$s$$$ because there is no other choice between the first chosen character and the last character of the second block and so on. Now if $$$\lvert t\rvert < n$$$, the first character that is in $$$c$$$ and not in $$$t$$$ is not present in the last remaining block (possibly empty) of $$$s$$$. So, the string subsequence matching algorithm fails and $$$c$$$ is not a subsequence of $$$s$$$.
Now, if $$$\lvert t\rvert=n$$$, we already know that $$$t$$$ is a subsequence of $$$s$$$. Now, the $$$i^{th}$$$ character in $$$t$$$ is the last character of the $$$i^{th}$$$ block of $$$s$$$, If you replace it with any other character, it will still be present in the $$$i^{th}$$$ block of $$$s$$$ since these blocks contain all the first $$$k$$$ English alphabets. So, no matter what changes you do to the string $$$t$$$, it will still remain a subsequence of $$$s$$$. This proves the second part.
Can someone help me guessing test case where this test solution failed [submission] I have tried all test cases that everyone has commented in the comment boxes
Take a look at Ticket 17314 from CF Stress for a counter example.
In DIV2C / DIV1A while building the counter-case, why is it always optimal to pick the first character as 'the one whose first index of occurrence in the given string is the highest'?
We can show that this construction will fail iff the string s is good (as defined in the problem)
Construction succeeds => string is not good
Construction fails => there exist at least n contiguous blocks with each block containing at least one instance of the first k chars. (ex. w = aabcbbcab can be grouped into [abc][abc]b). This form allows you to generate any subsequence of length n, so the string is good.
Your reason for special modulo at problem 2F/1C is preposterous at best. B is a rational number outside of modulo. What you are doing is childish smh.
Will-be-added-soon forces.
The contest was over about 4 days ago. However, the tutorials of 1E and 1B are still not updated. Just showing the code is confusing and meaningless.
Are you already forgotten this important Codeforces contest?
plz update it as soon as possible.
Hi, sorry for the delay, the editorial for all the problems have been added.
can somebody explain to me how do we get 7/9 on third sample of problem div2 D
Problem A and B were nice.
Hello A_G, Can you please explain your solution for D — Good Trip. Also it'll be helpful if you can explain how you are calculating and using inv array. Thanks!
nvm got the solution. But still curious about the way you've calculated inv array.243704107
https://codeforces.com/blog/entry/83075
Thanks a lot man!! Appreciate that:)
A simpler version of Div2C 1925C - Did We Get Everything Covered? on leetcode.
I never reached the first hint for 2B, this was my step to solution:
Searching for biggest
gwheres >= n.C. Strong Password
This formula can (probably) make div1E much easier:
Fix k. Let f(m,n) be the solution (expected number of cuts to make (m,n) -> (m0,n0) such that m0*n0<k). Then (if m*n>=k) f(m+1,n+1)+f(m,n)=f(m+1,n)+f(m,n+1). (How to prove? hint: try brute forcing to find f(m,n) then do basic algebra)
All we have to do left is try to handle base cases and reduce (m,n)
Sorry for my messy code (too many corner cases to cover, even had to generate random tests to catch all of them ;-;)
Happy Lunar New Year everyone ;)
Can somebody please explain to me what is trivial factorization?
In tutorial of 1/E, there seems to be a duplication in the multiplication of probability and I'm very confused. For example, in the first case I wonder why the conditional probability of lines from $$$reqv+1$$$ to $$$m-1$$$ is $$$\frac{1}{n+reqv} + \cdots + \frac{1}{n+m-2}$$$ instead of $$$\frac{1}{reqv+1} + \cdots + \frac{1}{m-1}$$$. Can someone help me?
"Keep adding this character to the counter-case until its length becomes n . This is a valid string which does not occur as a subsequence of s " can any one explain why this always true .
I don't know if anyone has noticed that 1D is very similar to the first example (algorithm P) of Knuth's TAOCP-4A-7.2.1.6. I think if you read it, the topic might become easier to understand.
Can somebody explain the third test case answer: (7/9)? I want exact calculations. I don't get, how they got this answer.
Problem B Can someone kindly explain the implementation showed in the solution?
Its like getting all divisors of x then among then getting the first number smaller or equal to x/n
Better solution for 2D. Good Trip:
If you use (xC2)*(kCx) = (kC2)*((k-2)C(x-2)), contribution of excursions becomes (kC2)/d^2. which can be calculated in constant time. So complexity is just taking inputs: O(m)
https://codeforces.com/contest/1925/submission/261739022
I solved 2D in O(t) time using linearity and arithmetic sum formula.
In div2 C why this approach is failing? The approach:i am mantaining a hashmap of char vs freq so now i traverse the string trying to take every char from first k char as my first char of string of NoAnswer then if other chars have freq more than or equal to n-count where count is the first char that has occured how many times
if at any time my condition fails that means answer is no with string as all chars same till a point then the char which failed the condn
No disrespect ,but atleast prove the goddamn claim you made in problem C, i mean it could be intuitive to you as author but there are low rated participants in these rounds too or if you dont consider them dont bother writing DIV2 rounds.
I am not getting in the case 1 How c(n + m, m) can give all valid sequence.
In terms of the final solution, you are saying that you will end up with a list of n+m symbols, and then whichever is smaller of those will determine the number of pairs possible.
To turn it into an actual number, there are n+m symbols and C(n+m,n) = C(n+m, m) = C(n+m,k) ways to arrange them. So the problem essentially says any arrangement works. Suppose we have two ( and two ), i.e. n=2, m=2, k=2.
The ways to arrange those symbols net of duplicates is 6: (()), ()(), ))((, )()(, )((), ())(.
I think only two of those allow constructing a subsequence of two balanced pairs. namely the first two. Which is not what formula gives.
yash_daga JaySharma1048576 mexomerf can you Please help with this ?