| Codeforces Round 144 (Div. 1) |
|---|
| Finished |
John Doe has an n × m table. John Doe can paint points in some table cells, not more than one point in one table cell. John Doe wants to use such operations to make each square subtable of size n × n have exactly k points.
John Doe wondered, how many distinct ways to fill the table with points are there, provided that the condition must hold. As this number can be rather large, John Doe asks to find its remainder after dividing by 1000000007 (109 + 7).
You should assume that John always paints a point exactly in the center of some cell. Two ways to fill a table are considered distinct, if there exists a table cell, that has a point in one way and doesn't have it in the other.
A single line contains space-separated integers n, m, k (1 ≤ n ≤ 100; n ≤ m ≤ 1018; 0 ≤ k ≤ n2) — the number of rows of the table, the number of columns of the table and the number of points each square must contain.
Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.
In a single line print a single integer — the remainder from dividing the described number of ways by 1000000007 (109 + 7).
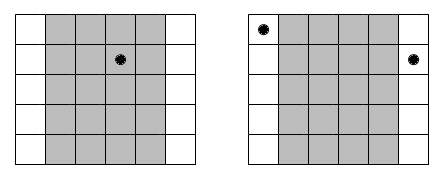
5 6 1
45
Let's consider the first test case:
| Name |
|---|




