It will be finised in few hours. If you don't understand something, ask your questions, please.
Idea: Gerald Implementation: tunyash Editorial: fdoer
Consider permutation p such that pi = i. Actually p is a sequence of numbers from 1 to n. Obviously ppi = i. Now the only trick is to change the permutation to satisfy the second equation: pi ≠ i. Let's swap every two consequtive elements. More formally, for each k: 2k ≤ n let's swap p2k - 1 and p2k. It's easy to see that the obtained permutation satisfies both equations for every n with the only exception: when n is odd, there is no answer and we should print - 1.
Idea: tunyash Implementation: tunyash, Gerald Editorial: fdoer
Firstly let's find the interval of possible values of s(x). Hence x2 ≤ n and n ≤ 1018, x ≤ 109. In other words, for every considerable solution x the decimal length of x does not extend 10 digits. So smax ≤ s(9999999999) = 10·9 = 90.
Let's bruteforce the value of s(x) (0 ≤ s(x) ≤ 90). Now we have an ordinary square equation. The deal is to solve it and to check that the current bruteforced value of s(x) is equal to sum of digits of the solution. If the solution exists and the equality holds, we should relax the answer.
It seems that the most error-generating part of this problem is solving the equation.
Knowing arrays is not neccessary to solve these two problems.
Idea: tunyash, fdoer Implementation: tunyash Editorial: tunyash
Let's add edge in order of increasing a and for equal b in order of increasing b (here a and b — the least and the greatest vertices of the edge). If the new edge adds too much 3-cycles, we won't add it. We can count the number of new 3-cycles in O(n) complexity (they all contain the new edge, so it's enough to check all variants of the third vertex). Obviously we will obtain some proper graph, because we can always add a vertex and two edges to make a new triangle. So, there is always an answer. The complexity of this solution is O(n3).
Let's proof that 100 vertices are always enough for the given restrictions on n.
- For some p after first p iterations we will have a complete graph of p vertices.
- Now we have exactly C(p, 3) triangles. Consider p such that C(p, 3) ≤ k and C(p, 3) is maximal.
- For the given restrictions p ≤ 85.
- From this moment, if we add u from some vertex, we increase the total number of 3-cycles on C(u, 2).
- So we have to present a small number that is less than C(85, 3) as sum of C(i, 2).
- The first number we subtruct will differ C(85, 1) on some value not greater than C(85, 1) = 85, because C(n, k) - C(n - 1, k) = C(n - 1, k - 1).
- The second number we subtruct will differ the number we have on some value not greater than C(14, 1) = 14.
- and so on.
- For every k it's enough to use not more that 90 vertices.
Idea: tunyash, Skird Implementation: tunyash Editorial: tunyash
- Let si number of points in the column i.
- Two neighboring squares are drawn at this picture, A is the number of point it the left area (it is one column), B is the number of points in the middle area and C is the number of points in the right area (it is one column too). That's why by definition we have:
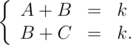
- Therefore A = C.
- That's why
- Divide all columns by equivalence classes on the basis of
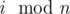 . For all a and b from one class sa = sb.
. For all a and b from one class sa = sb. - cnta is number of columns in class with
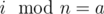 .
. - There are (Cnk)cnta ways to draw k points in the each of columns in the class a independendently of the other classes.
- dp[i][j] is number of ways to fill all columns in classes 1, ... i in such way that
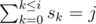 .
. 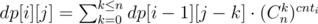
- cnti take only two values
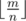 and
and 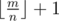 . Let's calc (Cna)cnti for all a and cnti and use it to calc our dp. We have O(n2·k) complexity.
. Let's calc (Cna)cnti for all a and cnti and use it to calc our dp. We have O(n2·k) complexity.
Idea: Gerald,tunyash Implementation: tunyash, Gerald Editorial: tunyash
Let's reduce the problem to the same problem for graphs with less orders. Vertex |D(n - 1)| + 1 is cutpoint (except cases n ≤ 2 but equations below is true for these cases).
Without loss of generality a < b.
Let dist(a, b, n) — length of the shortest path in graph of order n.
The first case is a ≤ |D(n - 1)| and |D(n - 1)| + 1 ≤ b
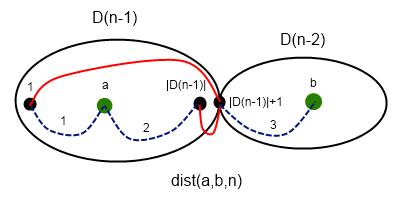
Edges is marked in red, paths is marked in blue. This formula means that we can go from the vertex a by the path 1 to the vertex 1. Then we can go to the |D(n - 1)| + 1 by the edge and go to the vertex b by the path 3. Or we can go to the vertex |D(n - 1)| by the path 2 and then go to the vertex |D(n - 1)| + 1 by the path 2 and then go to the vertex b by the path 3.
The second case is |D(n - 1)| + 1 ≤ a, b.
That's easy case.
The third case is a, b ≤ |D(n - 1)|
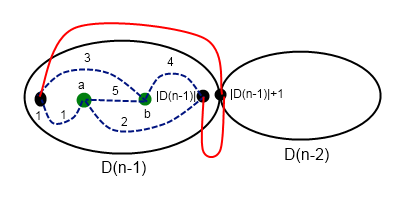
If shortest path contains cutpoint (|D(n - 1)| + 1) we can go to the vertex 1 or |D(n - 1)+1$ form the both of a and b. After that we can go to the cutpoint. Else we should consider path from a to b in D(n - 1).
Let's notice that for all of n will be no more than 4 distinct runnings of dist(i, j, n).
It can be prooved by the considering many cases of our actions.
In authors colution we cashed all dist(1, i, n) and dist(i, |D(n)|, n) for all achieveable i and n.
We have complexity 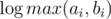 for one query. (it's log because |D(n)| grows like φn).
for one query. (it's log because |D(n)| grows like φn).
Idea: Gerald, tunyash Implementation: fdoer Editorial: fdoer
Let d and d' be arrays such that di = hi - hi + 1, d'i = - di for every 1 ≤ i ≤ (n - 1). With that notation the conditions of matching look somehow like these:
- the pieces do not intersect, that is, there isn't a single plank, such that it occurs in both pieces of the fence;
- the pieces are of the same width;
- for all i i (0 ≤ i ≤ r1 - l1 - 1) the following condition holds: dl1 + i = d'l2 + i (that is true in case when l = r).
The main idea of our solution is stated in the next sentence. For each query l...r the answer is number of pairs (a, b) such that (a > r or b < l), 1 ≤ a ≤ b ≤ n - 1, b - a = r - l and dl...r - 1 exactly matches d'a...b - 1. Let's build a suffix array sa from the concatenation of arrays d and d' with a fictive number between them for separation. Let position of suffix i in sa be posi. For each query all pieces of the fence that satisfy both second and third conditions of matching will be placed in sa on some segment boundleft...boundright such that boundleft ≤ posl ≤ boundright and lcp(boundleft...boundright) ≥ (r - l). So, it's possible to use binary search to find bound's. Depending on complexity of lcp finding algorithm, we could get them in O(logn) or O(log2n) complexity.
But there is still a problem to count the number of suffixes from saboundleft...boundright that satisfy the first condition too. Actually it is equal to count the number of i (boundleft ≤ i ≤ boundright) such that (n + 1 ≤ sai ≤ n + l - (r - l) - 1 or sai ≥ n + r) (in the concatenation d' starts from n + 1). It is a classic problem to count numbers from the given interval in the given subarray. For each query it could be solved in O(logn) complexity.
For instance, we could solve it offline using sweep line method and any data structure that support queries of sum on an interval and increment of an element. Or we could use some 2D/persistent structure.
So, the summary of the algorithm looks like this:
- build d and d'. Build a suffix array on their concatenation.
For each query:
- find the interval (boundleft...boundright) with two consecutive binary searches using lcp function.
- query the count of suffixes from that interval that do not intersect with the given piece of the fence.
The best author's solution complexity is O(nlogn + qlogn), but careful written solutions in O(nlog2n) comply with the lime limit too.
Idea: tunyash Implementation: tunyash, KAN Editorial: tunyash
Let's choose central column of the area and for all cells to the left from column calc masks of achieveable cells in the central column and for all cells to the right from column calc masks of cells of which this is achievable. It's easy dp with bitsets. 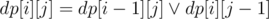 for the right part of board.
for the right part of board. 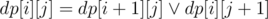 (
(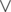 — logical or, here it's bitwise or for masks) for the left part. dp calcs mask of achieveable points in the central column.
— logical or, here it's bitwise or for masks) for the left part. dp calcs mask of achieveable points in the central column.

For query x1, y1, x2, y2 (if y1 ≤ mid ≤ y2, where mid is chosen central column) answer is yes if 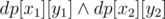 (
(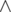 is bitwise and) is not empty.
is bitwise and) is not empty.
Run this algo for left and right part of board we will get answers for all queries. Complexity is 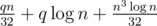 .
.










I believe there is an error in the DIV2 B problem. The range of s(x) should be 0 <= s(x) <= 81 because: sqrt( 10 ^18 ) = 10^9. So the biggest value s(x) will be when x = 10^9-1: s(x) = 9*9 = 81.
if s(x) <= 81 then s(x) <= 90, isn't it?
PRETTY MUCH YEAH BUT IT STILL DOES THE PART OF MAKING THE EXPLANATION CONFUSING.
For Div 2 A, there is no answer when n is odd, not only when n = 1.
Yes, you are right. Thank you.
deleted: sorry misunderstanding
why is it -1 for all odd numbers?
i can make something like this when n=3
3 1 2 here P1=3 P2=1 P3=2
we know Pp1=1 so by comparing p1=2 Pp2=2 so p2=3 and p3=1
so every condition is getting satisfied. why is it -1 then?
$$$P_{P_{i}}=i$$$, so $$$P_{P_{1}}=1$$$ but in your case $$$P_{1}=3$$$ so $$$P_{P_{1}}=P_{3}=2\ne{1}$$$ , hence the condition is false. Every node in this array forms a cycle with another node, so it will never be possible to solve it for odd $$$n$$$.
Thank you epsilon_573
p1 = 3, p2 = 1, p3 = 2 [p(i)!=i] P(p1) = 1 so P(3) = 1 P(p[i]) = i P(p2) = 2 so P(1) = 2 P(p3) = 3 so P(2) = 3 so our perfect permutation is : 2 3 1
what's Wrong?
in doe graphs problem. 1 6 1 13 for this input answer 2 but i dont understand.can someone explain me.pleas write path from 1 to 13
1 -> 14 -> 13
|D(13)|=?
sory |D(6)|=?
|D(0)| = 1, |D(1)| = 2, |D(2)| = 3, |D(3)| = 5, |D(4)| = 8, |D(5)| = 13, |D(6)| = 21
I'm having trouble understanding this part:
Thank you.
Look, we have some full graph. We add one vertex with q edges starting form it. Is it clear, that we added Cq2 triangles to our graph? It it's not, you may check it with pen and paper. Number of vertexes in full part of our graph is p and Cp3 ≤ k. p is maximal possible value such that Cp3 ≤ k. Therefore k ≤ Cp + 13 and k - Cp3 ≤ (Cp + 13 - Cp3. k - Cp3 ≤ Cp2. Ok? We add new vertex with q edges. We will add Cq2 triangles to our graph and q is maximal. Therefore k - Cp3 - Cq2 ≤ Cq1 = q. We have x = Cp3 + Cq2 triangles in out graph and difference with k is no more than q ≤ p ≤ 85. If we will repeat adding vertex five or six time difference between k and number of triangles will become zero.
Got it. Thanks!
Please check the last case of problem c div 1. There are some mistakes with the formula.
Where?
You lost a bracket. Is it before or after "+ 2"? ^^
Thank you, I see.
Didn't understand editorial for "Quick Tortoise". Somebody please explain in detail.
Basically, the simple way to solve this problem would be to precompute if it's possible to get from (x1,y1) to (x2,y2) for all possible (x1,y1) and (x2,y2). This would take O(n^4) time and space so with n as large as 500 it won't work.
The idea for speeding this up is to use divide & conquer. The editorial splits the board by columns, and I did it by rows in my solution (and that is probably more cache-efficient, although that doesn't really matter) — either way will work fine.
Imagine first that every query you get was such that (x1,y1) is in the top half of the board and (x2,y2) is in the bottom half of the board. Then you could answer each query by the following procedure: 1. find all the cells in the middle row of the board reachable from (x1,y1) 2. find all the cells in the middle row of the board from which you can reach (x2,y2) 3. you answer "Yes" iff the results of 1. and 2. intersect
You can precompute the answers for 1 and 2 using dynamic programming. As O(n) cells of the middle row could be reachable from any cell, you could use O(n^3) time and space to compute the answers for 1 and 2. Using a bit set (the bitset class in C++ for example), you can reduce that to ~(n^3)/32 assuming you implement the bit set as an array of 32-bit ints. So for subproblem 1, for each cell, you store a bit set that indicates if you can reach a certain column of the middle row or not. You can compute each bit set via two bit set operations by the rules of the game.
Now back to the original problem. If the query is not of the form discussed above, then it is either entirely in the top half of the board, or it is entirely in the bottom half of the board. Therefore, you build an almost-complete binary tree structure. At every node of this tree, you solve the same problem discussed above for a certain row-slice of the board. The depth of this tree is about lg(#rows). You can precompute this tree before any queries are processed.
Then, for each query, you just walk down the tree to the appropriate row-slice of the board and look up the precomputed answers to subproblems 1 and 2 and return the answer. For implementation details of exactly this idea, you can look at my solution http://codeforces.com/contest/232/submission/2471344.
I didn't understand the analysis of the solution of "Table" problem. Can anyone help me and explain it in more details please?
I have a different weird solution for 233B: after looking for x for many different n values, I have noticed that the answer is always close to sqrt(n) so I just looked for a suitable x from sqrt(n)-100 to sqrt(n)+100