| Codeforces Round 144 (Div. 1) |
|---|
| Finished |
John Doe decided that some mathematical object must be named after him. So he invented the Doe graphs. The Doe graphs are a family of undirected graphs, each of them is characterized by a single non-negative number — its order.
We'll denote a graph of order k as D(k), and we'll denote the number of vertices in the graph D(k) as |D(k)|. Then let's define the Doe graphs as follows:
- D(0) consists of a single vertex, that has number 1.
- D(1) consists of two vertices with numbers 1 and 2, connected by an edge.
- D(n) for n ≥ 2 is obtained from graphs D(n - 1) and D(n - 2). D(n - 1) and D(n - 2) are joined in one graph, at that numbers of all vertices of graph D(n - 2) increase by |D(n - 1)| (for example, vertex number 1 of graph D(n - 2) becomes vertex number 1 + |D(n - 1)|). After that two edges are added to the graph: the first one goes between vertices with numbers |D(n - 1)| and |D(n - 1)| + 1, the second one goes between vertices with numbers |D(n - 1)| + 1 and 1. Note that the definition of graph D(n) implies, that D(n) is a connected graph, its vertices are numbered from 1 to |D(n)|.
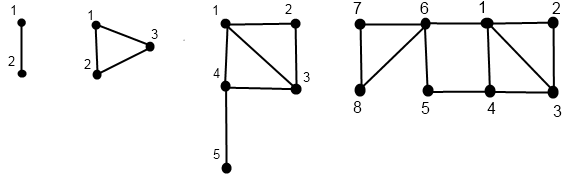 The picture shows the Doe graphs of order 1, 2, 3 and 4, from left to right.
The picture shows the Doe graphs of order 1, 2, 3 and 4, from left to right. John thinks that Doe graphs are that great because for them exists a polynomial algorithm for the search of Hamiltonian path. However, your task is to answer queries of finding the shortest-length path between the vertices ai and bi in the graph D(n).
A path between a pair of vertices u and v in the graph is a sequence of vertices x1, x2, ..., xk (k > 1) such, that x1 = u, xk = v, and for any i (i < k) vertices xi and xi + 1 are connected by a graph edge. The length of path x1, x2, ..., xk is number (k - 1).
The first line contains two integers t and n (1 ≤ t ≤ 105; 1 ≤ n ≤ 103) — the number of queries and the order of the given graph. The i-th of the next t lines contains two integers ai and bi (1 ≤ ai, bi ≤ 1016, ai ≠ bi) — numbers of two vertices in the i-th query. It is guaranteed that ai, bi ≤ |D(n)|.
Please, do not use the %lld specifier to read or write 64-bit integers in С++. It is preferred to use cin, cout streams or the %I64d specifier.
For each query print a single integer on a single line — the length of the shortest path between vertices ai and bi. Print the answers to the queries in the order, in which the queries are given in the input.
10 5
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5
4 5
1
1
1
2
1
2
3
1
2
1
| Name |
|---|




