| Codeforces Round 152 (Div. 1) |
|---|
| Finished |
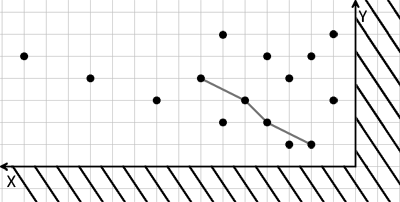
In the evenings Donkey would join Shrek to look at the stars. They would sit on a log, sipping tea and they would watch the starry sky. The sky hung above the roof, right behind the chimney. Shrek's stars were to the right of the chimney and the Donkey's stars were to the left. Most days the Donkey would just count the stars, so he knew that they are exactly n. This time he wanted a challenge. He imagined a coordinate system: he put the origin of the coordinates at the intersection of the roof and the chimney, directed the OX axis to the left along the roof and the OY axis — up along the chimney (see figure). The Donkey imagined two rays emanating from he origin of axes at angles α1 and α2 to the OX axis.
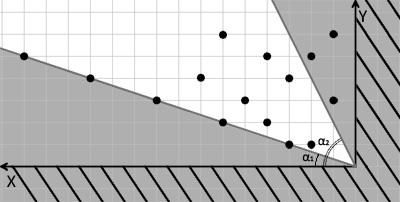
Now he chooses any star that lies strictly between these rays. After that he imagines more rays that emanate from this star at the same angles α1 and α2 to the OX axis and chooses another star that lies strictly between the new rays. He repeats the operation as long as there still are stars he can choose between the rays that emanate from a star.
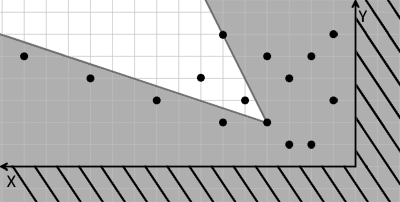
As a result, the Donkey gets a chain of stars. He can consecutively get to each star if he acts by the given rules.
Your task is to find the maximum number of stars m that the Donkey's chain can contain.
Note that the chain must necessarily start in the point of the origin of the axes, that isn't taken into consideration while counting the number m of stars in the chain.
The first line contains an integer n (1 ≤ n ≤ 105) — the number of stars. The second line contains simple fractions representing relationships "a/b c/d", such that 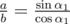 and
and 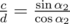 (0 ≤ a, b, c, d ≤ 105;
(0 ≤ a, b, c, d ≤ 105; 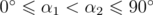 ;
; 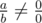 ;
; 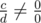 ). The given numbers a, b, c, d are integers.
). The given numbers a, b, c, d are integers.
Next n lines contain pairs of integers xi, yi (1 ≤ xi, yi ≤ 105)— the stars' coordinates.
It is guaranteed that all stars have distinct coordinates.
In a single line print number m — the answer to the problem.
15
1/3 2/1
3 1
6 2
4 2
2 5
4 5
6 6
3 4
1 6
2 1
7 4
9 3
5 3
1 3
15 5
12 4
4
In the sample the longest chain the Donkey can build consists of four stars. Note that the Donkey can't choose the stars that lie on the rays he imagines.
| Name |
|---|




