Группа из n городов связана сетью дорог. Первоначально между любой парой городов есть двунаправленная дорога, таким образом суммарное количество дорог равно 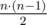 . Чтобы проехать по любой из этих дорог, требуется ровно y секунд.
. Чтобы проехать по любой из этих дорог, требуется ровно y секунд.
Остовным деревом называется такое подмножество дорог размера n - 1, что между любой парой городов можно проехать, используя только эти дороги.
Было выбрано некоторое остовное дерево. После этого время проезда по каждой дороге остовного дерева было изменено с y на x. Обратите внимание, не гарантируется, что x меньше y.
Вы хотели бы посетить все города по одному разу, используя кратчайший путь. Вам даны числа n, x, y и описание выбранного остовного дерева. Определите минимальное время, необходимое, чтобы посетить каждый город ровно один раз, если разрешается начать маршрут в любом городе и закончить также в любом городе.
В первой строке входных данных записаны три целых числа n, x и y (2 ≤ n ≤ 200 000, 1 ≤ x, y ≤ 109).
Каждая из следующих n - 1 строк содержит описание одной дороги остовного дерева. В i-й из этих строк записаны два целых числа ui и vi (1 ≤ ui, vi ≤ n) — индексы городов, соединённых i-й дорогой. Гарантируется, что эти дороги образуют остовное дерево.
Выведите единственное целое число — минимальное количество секунд, которое придётся потратить на путь, проходящий через каждый город ровно один раз.
5 2 3
1 2
1 3
3 4
5 3
9
5 3 2
1 2
1 3
3 4
5 3
8
В первом примере дороги в остовном дереве требуют 2 секунд, в то время как на другие дороги уходит 3 секунды. Один из примеров оптимального пути: 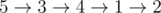 .
.
Во втором примере нам дано такое же остовное дерево, но дороги в нём требуют 3 секунд, в то время как остальные дороги требуют 2 секунд. Один из примеров оптимального пути: 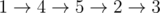 .
.
| Название |
|---|




