Тарли имеет два различных типа предметов, коробки еды и бочки вина. Есть f коробок с едой и w бочек вина. Тарли хранит их в разных стеках, и каждый стек может содержать только либо коробки еды, либо бочки вина, но не оба типа предметов сразу. Стеки расположены в ряд так, что нет двух стеков еды рядом, и нет двух стеков вина рядом.
Высота стека определена, как количество предметов в стеке. Два стека различны, если их высоты различны или один стек содержит еду, а другой вино.
Джону Сноу не нравится когда, какой-нибудь стек с вином имеет высоту меньше либо равную h. Какова вероятность, что Джону Сноу понравится расстановка в стеки, если все расстановки равновероятны?
Две расстановки стеков считаются разными, если существует такое i, что i-й стек одной расстановки не равен i-у стеку другой расстановки.
Первая строка входных данных содержит три целых числа f, w, h (0 ≤ f, w, h ≤ 105) — количество коробок с едой, количество бочек с вином и число h описанное выше. Гарантируется, что есть хотя бы одна коробка еды или хотя бы одна бочка вина.
Выведите вероятность того, что Джон Сноу понравится расстановка. Вероятность этого имеет форму  , вам необходимо вывести единственное целое число равное p·q - 1 mod (109 + 7).
, вам необходимо вывести единственное целое число равное p·q - 1 mod (109 + 7).
1 1 1
0
1 2 1
666666672
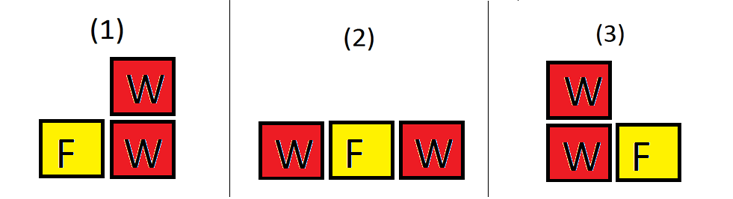
В первом тестовом примере f = 1, w = 1 и h = 1, здесь две возможных расстановки, и ни одна из них не нравится Джону Сноу.
Во втором тестовом примере f = 1, w = 2 и h = 1, здесь три возможных расстановки. Джону нравятся расстановки (1) и (3). Поэтому вероятность равна  .
.
| Название |
|---|




