768A. Oath of the Night's Watch
Set and Editorial by: vntshh
You just have to find the number of elements greater than the minimum number occurring in the array and less than the maximum number occurring in the array. This can be done in O(n) by traversing the array once and finding the minimum and maximum of the array, and then in another traversal, find the good numbers.
Complexity: O(n)
768B. Code For 1
Set and Editorial by: killer_bee
It is easy to see that the total number of elements in the final list will be 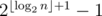 . The problem can be solved by locating each element in the list and checking whether it is '1' .The ith element can be located in O(logn) by using Divide and Conquer strategy. Answer is the total number of all such elements which equal '1'.
. The problem can be solved by locating each element in the list and checking whether it is '1' .The ith element can be located in O(logn) by using Divide and Conquer strategy. Answer is the total number of all such elements which equal '1'.
Complexity : O((r - l + 1) * logn)
768C. Jon Snow and his Favourite Number
Set and Editorial by: vntshh
The range of strengths of any ranger at any point of time can be [0,1023]. This allows us to maintain a frequency array of the strengths of the rangers. Now, the updation of the array can be done in the following way: Make a copy of the frequency array. If the number of rangers having strength less than a strength y is even, and there are freq[y] rangers having strength y, ceil(freq[y] / 2) rangers will be updated and will have strengths y^x, and the remaining will retain the same strength. If the number of rangers having strength less than a strength y is odd,and there are freq[y] rangers having strength y, floor(freq[y] / 2) rangers will be updated and will have strengths y^x, and remaining will have the same strength. This operation has to be done k times, thus the overall complexity is O(1024 * k).
Complexity: O(k * 210)
768D. Jon and Orbs
Set and Editorial by: arnabsamanta
This problem can be solve using inclusion-exclusion principle but precision errors need to be handled. Therefore, we use the following dynamic programming approach to solve this problem.
On n - th day there are two possibilities,
Case-1 : Jon doesn't find a new orb then the probability of it is  .
.
Case-2 : Jon does find a new orb then the probability of it is 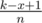 .
.
Therefore, 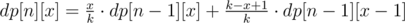
We need to find the minimum n such that 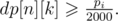
where,
n = number of days Jon waited.
x = number of distinct orbs Jon have till now.
dp[n][x] = probability of Jon having x distinct orbs in n days.
k = Total number of distinct orbs possible.
PS:The ε was added so that the any solution considering the probability in the given range 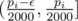 passes the system tests.
passes the system tests.
768E. Game of Stones
Set and Editorial by: AakashHanda
This problem can be solved using DP with Bitmasks to calculate the grundy value of piles. Let us have a 2-dimensional dp table, dp[i][j], where the first dimension is for number of stones in the pile and second dimension is for bitmask. The bitmask has k-th bit set if we are allowed to remove k + 1 stones from the pile.
Now, to calculate dp[i][j] we need to iterate over all possible moves allowed and find the mex.
Finally for the game, we use the grundy values stored in dp[i][2i - 1] for a pile of size i. We take the xor of grundy values of all piles sizes. If it is 0, then Jon wins, otherwise Sam wins.
The complexity of this solution is 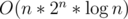 . This will not be accepted. We can use the following optimizations for this problem:
. This will not be accepted. We can use the following optimizations for this problem:
- Use a top-down approach to calculate the values of dp[i][2i - 1], hence calculating only those values that are required.
- Since we can only remove at most i stones from a pile, as stated above, we need to store values from j in range [0, 2i - 1].
So we can rewrite the above code to incorporate these change. Hence, the final solution is as follows
Bonus: Try to find and prove the O(1) formula for grundy values
768F. Barrels and boxes
Set and Editorial by: arnabsamanta, apoorv_kulsh
Every arrangement of stacks can expressed in the form of linear arrangement. In this linear arrangement, every contiguous segment of wine barrels are separated by food boxes. For the arrangement to be liked by Jon each of the f + 1 partitions created by f food boxes must contain either 0 or greater than h wine barrels.
Let u out of f + 1 partitions have non-zero wine barrels then the remaining r + 1 - u partitions must have 0 wine barrels..
Total number of arrangements with exactly u stacks of wine barrels are 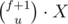
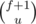 is the number of ways of choosing u partitions out of f + 1 partitions.
is the number of ways of choosing u partitions out of f + 1 partitions.
X is the number of ways to place w wine barrels in these u partitions which is equal to the coefficient of xw in {xh + 1·(1 + x + ...)}u. Finally we sum it up for all u from 1 to f + 1.
So the time complexity becomes O(w) with pre-processing of factorials.
w = 0 was the corner case for which the answer was 1.
We did not anticipate it will cause so much trouble. Not placing it in the pretests was a rookie mistake.
768G. The Winds of Winter
Set and Editorial by: apoorv_kulsh
We are given a tree. We remove one node from this tree to form a forest. Strength of forest is defined as the size of largest tree in forest. We need to minimize the strength by changing the parent of atmost one node to some other node such that number of components remain same.
To find the minimum value of strength we do a binary search on strength. It is possible to attain Strength S if
1. There is less than one component with size greater than S.
2. There exists a node in maximum component with subtree size Y such that,
M - Y ≤ S (Here M is size of maximum component and m is size of minimum component)
m + Y ≤ S.
Then we can change the parent of this node to some node in smallest component.
The problem now is to store Subtree_size of all nodes in the maximum component and perform binary search on them. We can use Stl Map for this.
Let X be the node which is removed and Xsize be its subtree size There are two cases now -:
1. When max size tree is child of X.
2. When max size tree is the tree which remains when we remove subtree of X from original tree.(We refer to this as outer tree of X).
In the second case the subtree sizes of nodes on path from root to X will change when X is removed. Infact their subtree size will decrease exactly by Xsize. While performing binary search on these nodes there will be an offset of Xsize. So we store them seperately. Now we need to maintain 3 Maps,
where
mapchildren : Stores the Subtree_size of all nodes present in heaviest child of X.
mapparent : Stores the Subtree_size of all nodes on the path from root to X.
mapouter : Stores the Subtree_size of all nodes in outer tree which are not on path from root to X.
Go through this blog post before reading further (http://codeforces.com/blog/entry/44351).
Maintaining the Maps
mapchildren and mapparent are initialised to empty while mapouter contains Subtree_size of all nodes in the tree.
mapparent : This can be easily maintained by inserting the Subtree_size of node in map when we enter a node in dfs and remove it when we exit it.
mapchildren : mapchildren can be maintained by using the dsu on tree trick mentioned in blogpost.
mapouter : When we insert a node's subtree_size in mapchildern or mapparent we can remove the same from mapouter and similarly when we insert a node's Subtree_size in mapchildern or mapparent we can remove the same from mapouter.
Refer to HLD style implementation in blogpost for easiest way of maintaining mapouter.
Refer to code below for exact point of insertions and deletions into above mentioned 3 maps.
Complexity O(NlogN2)











A pile in this custom game of size x can mapped to regular nim game pile of size j, such that j is the largest i where i * (i + 1) / 2 <= x holds.
This holds because each move you make on the custom pile can be expressed as a sum of one or more numbers <= j.
For example 10 = 1 + 2 + 3 + 4, and j here is equal to 4.
A move on this custom pile of size 5 can be expressed as 2 + 3.
Since we are only allowed to remove a certain quantity from a pile once, you can see that each custom move is equivalent to removing one or more numbers from a regular nim game pile of size j.
Now for multiple games, you xor them like regular nim.
Code that implements this idea : http://codeforces.com/contest/768/submission/24853749
I don't understand your proof of j being the Grundy number. Taking your example, if you have a pile of 10 and remove 5 you get a pile of 5 and you are allowed to take 1, 2, 3, 4 from it.
How is that equivalent to removing 2 and 3 from {1, 2, 3, 4}? I mean, in that case you would get {1, 4} and you could remove 1, 4 or 5 stones from it. Am I missing something?
I didn’t mean to construct a solution.I was only giving an example to give a sense of what i and j mean. For example one could pick {1,4} instead. It’s the amount of present stones in the respective piles that matter.
By the way this is not a proof.It's just a way to solve the problem.
Mistaken.
It is not as simple as that. Imagine 2 piles that have infinite stones but you can only take 1, 2, 3 from them. You can also imagine it as initially 2 piles of 21 and both players took 4, 5 and 6 from them so there are 2 piles of 6 stones where you can take 1, 2 and 3. There are 3 numbers from 1...j remaining but the nimber of these stacks is obviously 1 because they will simply waste 3 moves on each stack.
I solved this problem in a bit more than 6 minutes including reading the statement using this but now that aurinegro said that, I can't really even start a proof of the reason why it works.
Mistaken.
A pile of 6 where you can take 1, 2, 3 and a pile of 1 where you can take 1. First player loses. Edit: if it was like you said and "defined on number available moves left from {1,2,..,j}." it should be 1^3=2 and the first player should win. It is way more complex, you can go from lesser state to a greater state, it's not a simple mapping like "taking number greater than j means taking more than one stone".
Thanks. I've understand. I was balled-up by "Imagine 2 piles that have infinite stones but you can only take 1, 2, 3 from them." Example with 21 is concrete contrary instance, I've understood it later.
I think I got a reasonable proof:
First, from the definition of Grundy number (as a minimum excluded) it is not hard to see that for a state s such that Grundy(s) = k there must be a path s = sk → sk - 1 → ... → s1 → s0 where Grundy(si) = i. Since the number of stones taken in each step must be different, you have an upper bound for Grundy(n), namely the largest k such that 1 + 2 + ... + k ≤ n. Below, I will denote this k as k(n).
It is possible to prove equality by induction. Our states will be of the form (n, X) where n is the number of stones and X is the allowed moves (a set of integers) and the inductive hypothesis will be that for any state , Grundy(s) = k(n). You can verify that the base case is true, and for any k' < k(n) it is possible to reach a state
, Grundy(s) = k(n). You can verify that the base case is true, and for any k' < k(n) it is possible to reach a state  with k' = k(n'). This implies that Grundy(s) ≥ k(n) and together with the previous upper bound proves equality.
with k' = k(n'). This implies that Grundy(s) ≥ k(n) and together with the previous upper bound proves equality.
I've misunderstand proving equality by induction. What is X' ?
Inductive hypothesis is that for any n'< n and any X', Grundy(n',X')=k(n') ? And we want to prove for any X that Grundy(n,X)=k(n) ?
Well, I agree that my writing wasn't super clear.
The idea is to prove by induction in k that if 1 + 2 + ... + k ≤ n < 1 + 2 + ... + (n + 1), then the Grundy number of a position with n stones where the moves 1, 2, ..., k are allowed is exactly k. The set X' was used to show that other moves might be allowed as well, it is irrelevant.
It is not true that Grundy(n, X) = k(n) for any X.
tfg has wrote above: A pile of 6 where you can take 1, 2, 3 and a pile of 1 where you can take 1. First player loses. If Grandy for first pile is 3 then 1^3=2 and the first player should win.
Counter example to your proof:s={3,{1,2}}. Grundy value is 0.
Good job! Here's another approach:
Precompute the Grundy numbers offline using any brute-force solution and then just store them as an array :) 29436875
This works in under a minute because the number of banned masks is not too big.
Some people solved C by finding a cycle in the sequence of arrays of rangers: http://codeforces.com/contest/768/submission/24853717
Can this be hacked, or there is a way to prove that the cycle will never be too long?
This would be very interesting. I solved it using this approach, after I saw that the sequence will run into a cycle pretty quickly. I did a few thousand experiments using random numbers, and in each one I found the cycle after max 5 operations. Although I have no idea how to prove this.
Maybe it's because of how freq[x] could only oscillate between 6 values, and it's also bounded by sum(freq[x], freq[x^x'])? I am still not sure what makes all freq[x] oscillation consonant that east though.
B can be done in O(max(r-l, logn)) when I reverse n first and use lsone.
In problem D how we can estimate max value of n for given k ?
Overestimate and test 1000 orbs and p = 1000
I asked estimation for given k.
I think n=klogk is legit enough (because the expected number of days to achieve full kind of orb is klogk). This result is here. https://en.wikipedia.org/wiki/Coupon_collector's_problem
Thanks. It's kinda sad that the authors of this round did not mention (intentionally?) this proof in their editorial, because it is probably the most interesting part of the problem.
In D, aren't you considering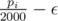 instead of
instead of 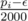 ? Is that correct?
? Is that correct?
Edit: nevermind, got it.
I have no idea why this code can pass problem C. I just Simulate these operations until the timeout or the number of steps exceeds k. QwQ http://codeforces.com/contest/768/submission/24857855
I'm guessing that in all large test cases, the first and last element stop changing, so you can just stop simulation early. This hack should break it, depending on where the sim stops: 99999 99999 7 1 2 2 2 2 .....
B can be solved in O(max(log n,log r))
Hi, I want to share my
O(logn)solution for Problem B.24858905We can observe some interesting phenomenon:
The list is Palindrome.
Let
len(n)means the length of the final list, then len(n) = (1«bitcount(n)) - 1.There are exactly n 1s in the final list(This can be proved by Mathematical Induction).
let
f(n, x)means the number of 1s in the first x elements,so the answer is f(n, r) - f(n, l - 1).We can calculate it recursively:
if x < len(n / 2), f(n, x) = f(n / 2, x)
if x = len(n / 2) + 1, f(n, x) = (n / 2) + (x mod 2)
if x > len(n / 2) + 1, f(n, x) = (n / 2) + (x mod 2) + f(n / 2, x - len(n / 2) - 1)
Sorry for my bad English ;)
For third case when x > len(n / 2) + 1: f(n, x) = (n / 2) + (x mod 2) + f(n / 2, x - len(n / 2) - 1)
You're right! Fixed.
HELPPP PLEASE
REGARDING PROBLEM C, I submited three identical solutions but with different results wrong , right1 and right2. The only difference is the vector size (1025, 1024 and 1500 respectively). all should work since the problem uses only the first 1024 slots.
I suppose it is some kind of undefined behaviour, can someone please help me? this is driving me crazy...
for(int i = 0; i<v[ATUAL].size(); i++) .. v[OUTRO][i^x] += ..
i^x can be greater than size unless size is a power of 2.
For problem D editorial, is x/n supposed to be x/k?
Can anyone explain how this function works?
Can anyone explain in details X value in F editorial?
I solve problem C in the following way: I have a two-dimensional array[1024][100000] which I use to save the state of the array after i operations.I update the array in an easy way: 1) First I sort the elements. 2) Then I iterate through the array and update each element This process takes O(nlgn) time, and I do it 1023 times so my algorithm works in O(nlgn*1023)times in total. after that if k<=1023 I print array[n-1][k] and array[0][k] which are the maximum and minimum values after k operations. otherwise when k>1023 I iterate through the first 1023 states of the array and find a repeated state. Then using this repeated state I find the period of the operation and at last find the state of the array after k times, without doing the operation k times, but only with computing the first 1023 operations. My solution worked and got accepted but I didn't prove that we reach a repeated state after a maximum of 1023 operations. Can anyone prove it for me?
I solved problem C in direct way as problem statement, only use k % 64 instead of k.
code 24870180
Q: Is this correct solution or I AC because weak tests???
3 64 1023
1 2 3
Answer : 1021 1
Thx, a lot!!!
Can provide a test for k% 256 ? )
Just change k to 256 lol.
here is my code. Your text to link here...
"For the arrangement to be liked by Jon each of the f + 1 partitions created by f food boxes must contain either 0 or greater than h wine barrels"- I don't get the "must contain either 0 or..." part. Is it possible for a stack to be empty?
In problem D,
Case-1 : Jon doesn't find a new orb then the probability of it is x/k
Case-2 : Jon does find a new orb then the probability of it is k-x+1/k;
I could not get why it is k-x+1 , shouldn't it be k-x , so that x + (k-x)=k
Got it,Thanks.
The new orb is the
xth one. So before finding it he has alreadyx-1different orbs, and there arek - (x - 1)possible new orbs.Thank you for your support.
Then shouldn't probability of finding an old orb be (x-1)/k. Sorry, i am still confused.
No, it should be x/k. We want to compute the probability that we have
xorbs afterknights. So either we find a new one in thek-th night (than this is thex-th one =>(k - (x - 1)) / k. Or we don't find a new one (so we already havexorbs =>x / k).Nevermind.
For Problem B final length should be 2^(1+floor(logN)) -1
For problem D, actually there is a solution O(qnlog^2)!!! Which is O(nlog^2) per query! 24861344 Actually c++ make it hard to accept it at contest!
Good Luck :) I Can't Accept it during the contest :)
can you please explain your solution?
Wondering how to use inclusion-exclusion principle to solve D? Already understood the dp solution, but how can it handle the precision error?
In problem F will be a solution if w is less than 10^9?Thanks.
The link ("Go through this blog post before reading further http://codeforces.com/blog/entry/44351") is not working, please fix it.
Fixed.
My O(r - l) solution for B:
Let x be the number from which we are generating this sequence.
We can see that is equal to the least significant bit of x (i.e.
is equal to the least significant bit of x (i.e.
floor(x / 2) == x >> 1andx & 1). We can also see thatx >> p == (x >> p) & 1, where p is the position of the most significant bit of x minus one.Now let's search for a pattern in the number of bits shifted every time.
Example for x = 7: If k is the number of bits shifted every time to obtain
(x >> k) & 1, we can see that k follows this pattern: 3, 2, 3, 1, 3, 2, 3, 0, 3, 2, 3, 1, 3, 2, 3. Here, we can observe that this looks a lot like the binary carry sequence. (See 743B - Chloe and the sequence ) The difference is that if p is the position of the MSB of x minus one, we are computing p - ai, where a is the binary carry sequence. We already know that we can compute any element of this sequence in O(1), therefore the problem is solvable in O(r - l).Code: 24878823
can someone please tell what is wrong with this solution of problem C
http://codeforces.com/contest/768/submission/24880646
instead of this: else if(c%2==0)cou++;
change it to this: else if (c % 2 == 0 && fre[i] % 2) cou++;
If the amount before you is even and your frequency is odd, then you take one more. If your frequency is even you always take only half, no more than that.
I want to share my solution to problem B
You can interpret the final list as a full balanced binary tree, because every node that has a element whose x>1 becomes two identical nodes (the children that are x/2) plus the original value is replaced by x mod 2. So you can index each node as shown in the image below for the example of n=10.For every index you can get the final value that is x mod 2 in O(lgN). (you start from the root that is the original value n (and is located in the middel index) and you can easily go to any other node and find its value and index as shown in this code here)
"One doesn't simply try Problem B with Full Balanced Binary Search Tree"
Just asking, is it ok to include precalculated values into the code? Just like the grundy values in the problem E one could get an AC solution by calculating the grundy values locally and then submit a solution using a lookup table cropped from it. Is this allowed in CF, or even in ACM?
Why not? Most of the accepted solutions have done this only. Google Code Jam specifically mentions that you should also submit code that you used to generate the pre-computed values, though there is no such restriction on CF and in ACM I think.
I was looking through solutions of A which failed sys tests but wasn't hacked. And I just can't understand why this solutions failed sys tests. Can someone explain?
???
lul. thanks )
Better question how this passed all pretests? :3
Answer is Because all the answer of the pretests was just n - 2
Any ideas why this fails for problem B?
It seems the numbers are too big for long long.
Update: I found my mistake.
Can someone explain why the change bottom up to top down can improve complexity of problem E?
Isn't it the same if all piles has 60 stones?
In problem B use something like Segment Tree Query, knowing that the number n will have n 1's. You can see my code here: http://codeforces.com/contest/768/submission/24840947 Fast and easy to code. :)
Time Complexity doubt related to Problem C : What I've read is 10^6 to 10^7 are the operations performed per second(in WORST CASE).Time limit for this problem was 4 seconds, that amounts to, say 4*(10^7) operations. Editorial code suggests some order of 10^8 operations. This suggests that passing the questions depends on processor capabilities. Can someone explain me this thing.
Thank you. vntshh
In 1 second, around 108 to 2 * 108 operations are possible. Time limit was set 4 seconds so that, the codes written in JAVA (generally takes the maximum time) also fit within the time limit.
What is the final complexity for problem E, since n * 2n * log(n) doesnt work?
O(1) there is regulation for the grundy values 0,1,1,2,2,2,3,3,3,3,4,4,4,4,4.... the value i appears i+1 times so we can find the grundy value for n by binary search or solve the quadric equation.
There is a nice pattern I got as an intiution for in C. And it allows one to generalise the problem for arbitrary values k and x. There is an inherent cyclic pattern that the array a follows. I got this intuition as(all values in the final array are either some a_j or a_i XOR x and a_i XOR x XOR x XOR x = a_i XOR x which might lead to repeated values).I ran a naive loop for small values of k and the cycle seemed to be of length 2. It does indeed give an AC.
Anyone with some clever proof of the same? Here is my submission. https://pastebin.com/ABsq7dJA
How can we prove the direct formula for grundy numbers in problem C ?