Introduction
Often in Competitive Programming, we have to choose between multiple algorithms/ approaches for a problem. How do we decide which algorithm is better and which algorithm to go for? Runnning an algorithm comes at the cost in the form of time taken or memory consumed. In this blog, we will try to compare algorithms or approaches based on their Time Complexity, which simply put is the time taken by them to run.
So how do we compare the algorithms? Do we calculate the exact time taken by them to run? Or do we try to predict the time taken based on our input? These approaches to calculate Time Complexity can be called as Experimental Analysis and Theoretical Analysis respectively. =========================================================================================================
Big O Notation
The Big O Notation ($$$O()$$$) provides a mathematical notation to understand the complexity of an algorithm or to represent the complexity of an algorithm. So, the idea is that time taken for an algorithm or a program to run is some function of the input size (n). This function can be quadratic, exponential, linear, logarithmic or even a constant function. For example, let us take a function whose time varies as $$$an^2 + bn + c$$$ (a, b, c are arbitrary constants). If we wanted to represent the time complexity of this function using big O notation, it would be $$$O(n^2)$$$. As seen in this example, for the notation, we ignore the constants and take only the highest power of n (while dropping it's constant coefficient).If the work can be done in constant time (like assigning a variable name, adding two integers, taking input / output), the complexity is said to be $$$O(1)$$$. Thus, to sum it up Big O notation is generally used to indicate time complexity of any algorithm. It quantifies the amount of time taken by an algorithm to execute as a function of the length of the input size. It removes constant factors so that the running time can be estimated in relation to n. the Big O notation is for the upper bound assessment and is the worst case consideration of the time complexity.
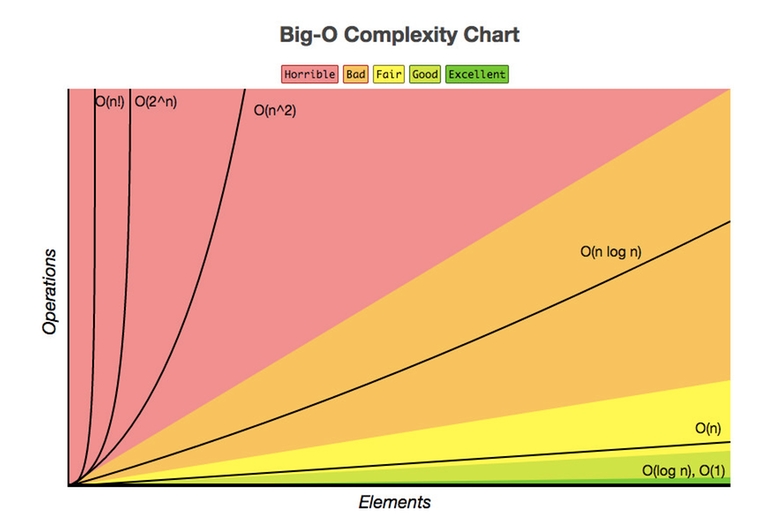
The following is the graphical representation of the number of primitive operatons vs input size of some of the common time complexities that one may come across — (This is the cleanest graphical representation I could find, and I got it from This LinkedIn Post)
=========================================================================================================
Experimental Analysis
In C++, we have a header file named ctime that allows us to check the the approximate processor time that is consumed by the program using the clock() function defined inside it. We already know that there are multiple sorting algorithms that we can use to sort a vector. Let us compare the builtin C++ STL sort with the Bubble Sort. Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in the wrong order.
Running this code on my device gives the following results :
From these observations, we can clearly see that the inbuilt sort in C++ STL is much faster. The STL sort has an average time complexity of $$$O(N \cdot log(N))$$$ while the Bubble Sort has an average time complexity of $$$O(N ^ 2)$$$. The time taken by Bubble Sort for $$$n = 1e5$$$ clearly shows how slow an $$$O(N ^ 2)$$$ program is when compared to an $$$O(Nlog(N))$$$ program. We can see that as the input size goes from $$$1e3$$$ to $$$1e4$$$ and from $$$1e4$$$ to $$$1e5$$$, the time taken by Bubble sort increases by a factor of $$$\approxeq 100$$$ each time, thus justifying it's $$$O(N ^ 2)$$$ complexity.
=========================================================================================================
Theoretical Analysis
Now that we have seen an example of experimentally getting the time taken by a program / algorithm to run, we can move on to theoretically predicting the time complexity of a program based on the number of primitive operations performed by the program for a given input size. Let us go over some cases and try to understand this.
- Simple For Loop
This is a basic for loop that goes over each of the n elements individually of something like a vector. The work inside the loop is being done in constant time ($$$O(1)$$$). Hence the complexity of this code will be $$$O(n)$$$ since it is performing n iterations to go over all the elements.
- Two non — nested loops
The time complexity of this code is $$$O(N + M)$$$.
- Nested Loop — Example 1
This time, we are having two loops, the second one being nested within the first. Let us see how many times the the inner loop runs for a given value of i as i itself iterates from 0 to n. When $$$i = 0$$$, the inner loop runs $$$n$$$ times; when $$$i = 1$$$, the inner loop runs $$$n - 1$$$ times and so on ($$$n - k$$$ iterations for $$$i = k$$$). At the end when $$$i = n - 1$$$ the inner loop will run only once. So we can find out the total iterations by summing each of these individual iteration counts:
Using the formula for summation of natural numbers, we can then write:
Visibly, the highest power of n here is 2, and thus we can say that these nested loops constitute a time complexity of $$$O(n^2)$$$.
- Nested Loop — Example 2
Let us take a 2nd example of a nested loop. It is tempting to think that it should be $$$O(n^2)$$$ since it is a nested loops, but that would be wrong. Let us assume values for n and k to make things simpler to understand. Say $$$n = 50, k = 5$$$. Now each time the inner loops completes one cycle of iterations, we will have $$$j = k$$$. Thus, in the first for loop (for(int i = 0; i < n; i = i + j)), j can be replaced with k each time the inner loop completes running. This means everytime we increment i, we take a jump of k. For our assumed values, we will get the different values assumed by i to be $$${0, 5, 10, ..... ,45}$$$. Thus, the outer loop will run $$$\lfloor (n / k) \rfloor$$$ times and thus has a time complexity of $$$O(\lfloor (n / k) \rfloor)$$$. The inner loop runs k times before we have another iteration of the outer loop, and thus has a time complexity of $$$O(k)$$$ each time it runs. Since the inner loop runs $$$\lfloor (n / k) \rfloor$$$ times, the total time complexity becomes $$$O({\lfloor (n / k) \rfloor} \cdot k)$$$ which is nothing but $$$O(n)$$$.
- Nested Loops — Example 3
Now the above code is another example of a nested loop. When we run the above code for an input of $$$n = 100$$$ we get the following output
So the output is approximately $$$2n$$$, and hence this code will have a time complexity of $$$O(n)$$$. Let us now try to see how it's coming out to be 1. The number of iterations performed by the outer loop is $$$\lfloor (\log_{2} n) \rfloor + 1$$$. And for the $$$k^{th}$$$ $$$(0 \leq k < \lfloor (\log_{2} n) \rfloor + 1)$$$ iteration of the outer loop, the inner loop will perform $$$\frac{n}{2^k}$$$ iterations. The cumulative time complexity hence comes out to be $$$O(n)$$$.
- Binary Search
Binary search is a fast searching algorithm that finds the index of a given target element in a sorted array. The steps to perform binary search are as follows:
1. Begin with the mid element of the whole array as a search key. 2. If the value of the search key is equal to the item then return an index of the search key. 3. Or if the value of the search key is less than the item in the middle of the interval, narrow the interval to the lower half. 4. Otherwise, narrow it to the upper half. 5. Repeatedly check from the second point until the value is found or the interval is empty.
Let us now see the code for Binary Search once (both iterative and recursive approaches):
Now, we move on to understand the Time Complexity of Binary Search. We can understand that after each iteration the size of the array gets halved. So after $$$k$$$ iterations, $$$n = \frac{n}{2^k}$$$. We are continuing to iterate until we have n = 1; i.e., we are left with the target element. So when we are the left with only the target element, the number of iterations $$$k$$$ is $$$\log_{2} n$$$ $$$( \because \frac{n}{2^k} = 1)$$$. Now, we can write $$$\log_{2} n$$$ as $$$\log_{2} b \cdot \log_{b} n$$$ where $$$\log_{2} b$$$ is a constant w.r.t $$$n$$$. Hence, the standard is to drop the base while considering the Big O notation and consequently the time complexity of Binary Search algorithm is said to be of the order $$$O(\log n)$$$. This time complexity is the reason why Binary search is considered to be so fast. $$$\log n$$$ goes very slowly over the values of $$$n$$$. Say we have an online judge which can perform $$$10^7$$$ iterations per second. We are given a sorted array and are told to find a target element. For linear search, in the worst case, we will have to perform all $$$10^7$$$ iterations which will take 1 second. But, if we use Binary search, we will need at most 24 iterations, which will take only $$$24 \cdot 10^{-7}$$$ second.
=========================================================================================================
Recurrence Relations
As many algorithms are recursive in nature, it is natural to analyze algorithms based on recurrence relations. Recurrence relation is a mathematical model that helps us compute the time complexity of an algorithm. We will first have a look at the substitution method of solving Recurrence relations, and then have a look at Master Theorem.
- Substitition Method
Let $$$T(n)$$$ be the worstcase time complexity of the algorithm with n being the input size. Now let us take a few examples —
Linear Search — Here, let $$$T(n)$$$ be the number of comparisons (time) required for linear search on an array of size n. If $$$n = 1$$$, $$$T(1) = 1$$$. Then, $$$T(n) = 1 + T(n − 1) = 1 + · · · + 1 + T(1)$$$ and $$$T(1) = 1$$$. Therefore, $$$T(n) = n − 1 + 1 = n$$$, i.e., $$$T(n) = O(n)$$$
Binary Search — Here, in each iteration, the size of the problem is halved by discarding either the lower or the upper half of the array. Recurrence relation is $$$T(n) = T(n/2) + 1$$$, and or $$$T(\frac{n}{2^x}) = T(\frac{n}{2^{x + 1}}) + 1$$$ for $$$x \geq 0$$$; where where $$$T(n)$$$ is the time required for binary search in an array of size n. Now, $$$T(n) = T(\frac{n}{2^k}) + 1 + ..... + 1$$$. Since $$$T(1) = 1$$$, when $$$n = 2^k$$$ we have; $$$T(n) = T(1) + k = 1 + \log_{2} n$$$. Now $$$\log_{2} n \leq (\log_{2} n + 1) \leq 2 \cdot \log_{2} n$$$ $$$ \forall n \geq 2$$$. Hence, we get, $$$T(n) = \log_{2} n$$$.
In the above analysis of Binary search we assumed that $$$n = 2^k$$$. So the question may arise if the analysis will hold true if $$$n \neq 2^k$$$. If the input array of size n is such that $$$n \neq 2^k$$$; then we can augment the least number of dummy values so that $$$n \neq 2^k$$$ for some k. For this modification, the size of the the array becomes at most $$$2n$$$. This approximation does not change our asymptotic analysis as the search time would be one more than the actual search time. That is, instead of $$$\log_{2}$$$ we are getting $$$\log_{2} {2n}$$$ which is $$$\log_{2} + 1$$$. Hence our analysis still holds as in symptotic sense, it is still $$$O(\log_{2} n)$$$.
Merge Sort — Merge Sort is a Divide and Conquer based sorting algorithm. What it does essentially is to divide the array into two equal sub arrays and sort each sub array recursively. It does the the sub-division operation recursively till the array size becomes one. To combine two sorted arrays of size $$$\frac{n}{2}$$$ is we need $$$\frac{n}{2} + \frac{n}{2} - 1$$$ or $$$n - 1$$$ comparisons in the worst case. The recurrence for the merge sort is,
When $$$n = 2^k$$$; we have;
Using the formula for the sum of a Geometric Progression we have
Also, here $$$T(1) = 0$$$ as there will be no comparison required when $$$n = 1$$$.
- Master Theorem When analyzing algorithms, recall that we only care about the asymptotic behavior. Recursive algorithms are no different. Rather than solve exactlythe recurrence relation associated with the cost of an algorithm, itis enough to give an asymptotic characterization. ther Master Theorem is a tool that allows us to get our answer without going through the recurrence relations each time. Let $$$T(n)$$$ be a monotonically increasing function satisfying the conditions $$$T(n) = a \cdot T(\lceil \frac {n}{b} \rceil) + f(n)$$$ ; where $$$a > 0$$$; $$$b > 1$$$, $$$f(n) \in O(n^d)$$$ and $$$d \geq 0$$$. The ceiling used for $$$\frac {n}{b}$$$ might as well be a floor or not be there at all if n was a power of b. Then, depending upon the relation between a, b and d; we can have the following solutions:
$$$T(n) = O(n^d)$$$ if $$$d > \log_{b} {a}$$$
$$$T(n) = O(n^d \cdot \log {n})$$$ if $$$d = \log_{b} {a}$$$
$$$T(n) = O(n^{\log_{b} {a}})$$$ if $$$d < \log_{b} {a}$$$
However, Master Theorem cannot be applied for all recurrence relations; and cannot be used if
$$$T(n)$$$ is not a monotone. (Ex: $$$T(n) = cos(n)$$$).
$$$f(n)$$$ is not a polynomial. (Ex: $$$T(n) = 2T(\frac{n}{2}) + 2^n$$$).
b cannot be represented as a constant (Ex: $$$T(n) = T(\sqrt{n})$$$)
=========================================================================================================
Time Complexity during problem solving
During problem solving on online judges, each problem will have a time limit that the submitted solution must obey. If it doen't run within the time limit, the judge will show a Time Limit Exceeded (TLE) error. Usually online judges can perform $$$10^7 - 10^8$$$ operations in one second. Most people consider $$$10^8$$$ operations per second to be a rule of thumb. Operations executable also varies from lanuguage to language and also depends on the operation beinbg performed. Array accesses, additions, bitshifts, multiplies, subtractions or xors are faster than mods or divisions. If we are doing hashmap lookups, or reading input/ printing output; approximately $$$10^6$$$ of these operations can be performed in a second. Based on the input size, we must determine the simplest solution that can run under the given time constraint and produce the correct answer. Let us consider an online jusdge that can perform $$$10^7$$$ operations in one second, and we are told to sort an array of size $$$10^4$$$. We will not be able to use a sorting algorithm that has a time complexity of $$$O(n^2)$$$ (like Bubble / Selection / Insertion sort). They could need upto $$$10^8$$$ operations to sort the array, which would take the online judge 10 seconds to complete. We would have to use an $$$O(n \cdot \log_{2} n)$$$ algorithm (like Merge Sort). For these, it becomes handy to keep in mind the time complexities of the algorithms we learn as we progress in our competitive programming journey.
Some examples of such time complexities could be (written in reference to the book Competitive Programming 3 by Steven and Felix Halim):
- $$$O(n!)$$$ : Enumerating permutations
- $$$O(2^n \cdot n^2)$$$ : DP TSP (Traveling salesman problem)
- $$$O(2^n \cdot n)$$$ : DP with bitmask technique
- $$$O(n^4)$$$ : DP with 3 dimensions + $$$O(n)$$$ loop; 4 nested loops;
- $$$O(n^3)$$$ : Floyd Warshall’s Algorithm
- $$$O(n^2 \cdot \log_{2} n)$$$ : 2-nested loops + a tree-related DS
- $$$O(n^2)$$$ : 2-nested loops; Bubble/ Selection/ Insertion Sort
- $$$O(n \cdot \log_{2} n)$$$ : Merge Sort / Heap Sort
- $$$O(n)$$$ : Search an element from a linear array; Traverse a linear array, building Segment Tree
- $$$O(\log_{2} n)$$$ : Binary Search
- $$$O(1)$$$ : Accessing an element from array by index; Arithmetic Operation; Push/ pop on a fixed-sized stack
Now, C++ provides us a lot of inbuilt functions that allow us to sort an array / find an element in an array and so on. While coding a solution it is helpful to keep in mind the time complexities of these built in functions as well. Say for example, the lowerbound and upperbound functions work with a time complexity of $$$O(\log n)$$$ since they are based on binary search. It is worth going through This Github Page for this.
- Sum of N over all test cases
Upto here, we have been looking at the time complexity for a problem with one test case; or the time complexity of each individual test cases when a problem has multiple test cases. Some problems however, will have a statement like "It is given that sum of N over all test cases does not exceed $$$10^9$$$". We shall now try to understand the significance of this line in a problem statement. Say we have a problem statement where $$$1 \leq t, n \leq 10^5$$$ and The sum of n over all testcases does not exceed $$$10^7$$$ with a time limit of 1 second. Now, let us consider that we can code a solution where the time complexity of each individual test case is $$$O(n)$$$. Then the overall time complexity of the solution will be $$$O(tn)$$$, which should not pass the time limit of 1 second since in the worst case $$$t \cdot n = 10^10$$$. However, in our example, the solution will still be accepted. Because when we are assuming the time complexity to be $$$O(tn)$$$, we are actually wanting to consider the sum of the individual values of n for each of the t test cases. This sum of n over all test cases has already been told to be within $$$10^7$$$, and an $$$O(10^7)$$$ solution passes the given time limit.
=========================================================================================================
There are some very interesting sites like VisuAlgo, CS USF and Algorithm Visualizer which have really fun animated visualizations of some data structures and algorithms :).
This is my first time writing something on CF blogs, and I expect to have made a handful of mistakes in this attempt. Any criticism / advice is welcome :D. I will try to improve my use of Latex / markup with time.