The algorithm of Tarjan is used to solve some problems which is about the connectedness of the Graph. Today I am going to introduce the key to solving E-DCC by Tarjan.
This problem is the template of E-DCC.
Defination : What is E-DCC?
The full name of E-DCC is edge double connectivity component.
Some people call it EBC (Edge Biconnected Component).
An E-DCC is a component that you cut any one of the edges, the graph is still connected.
For example, in this graph, nodes in same color are in the same E-DCC, and there are $$$3$$$ E-DCCs in this graph. They are:
node $$$1$$$
node $$$2$$$, $$$3$$$, $$$4$$$, $$$5$$$, $$$6$$$
node $$$7$$$

Solution : How to find E-DCC by Tarjan?
Bridge
First, we should know what BRIDGE is. - A bridge is an edge in the graph, and if you cut the edge off, the graph is not connected.
Tarjan
Tarjan is one of the algorithms which can solve this problems.
First I am going to introduce two arrays to you:
$$$low_x$$$: An array of trace values representing the minimum idx of points on a search tree rooted at $$$x$$$ which can be reached by only one edge which is not in the search tree.
$$$dfn_x$$$: Timestamp array, representing the order it was visited.
For example we can get the two values of the nodes:
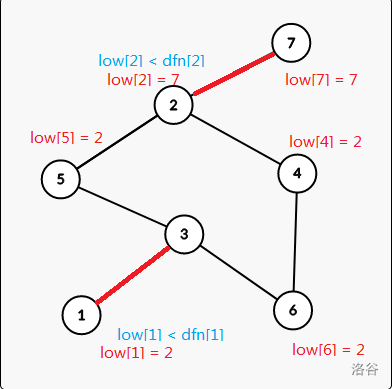
How to calculate $$$low_x$$$?
We assume that there is an undirected edge from the node $$$x$$$ to the node $$$y$$$. There are two conditions:
- First: If node $$$y$$$ is a node of the subtree of node $$$x$$$, so
low[x] = min(low[x], low[y]); - Secound: Else
low[x] = min(low[x], dfn[y]);
Node that: In the secound condition, it is $$$dfn_y$$$, and it isn't $$$low_y$$$.
We should look back to the defination:
by only one edge which is not in the search tree
Only one edge!
How to find Bridges?
If the undirected edge from x to y is a Bridge, if and only if (necessary and sufficient conditions) $$$dfn_x \lt low_y$$$.
Lets look back to the example:

For node $$$2$$$, $$$dfn_2 = 2$$$ and $$$low_2 = 7$$$, so edge (2 -> 7) is a bridge.
Because if the edge was cut, we can not goes back to node $$$7$$$ from node 2.
// code of finding bridges
void tarjan(int node, int in_edge)
{
dfn[node] = low[node] = ++id;
for (int i = head[node]; i; i = e[i].nxt)
{
const int to = e[i].to;
if (dfn[to] == 0)
{
tarjan(to, i);
if (dfn[node] < low[to])
b[i] = b[i ^ 1] = 1;
low[node] = min(low[node], low[to]);
}
else if (i != (in_edge ^ 1))
low[node] = min(low[node], dfn[to]);
}
}
E-DCC
If you know how to find Bridges, it will be easy for you to find all the E-DCC.
Cut all the bridges off, then we can get all the E-DCC.
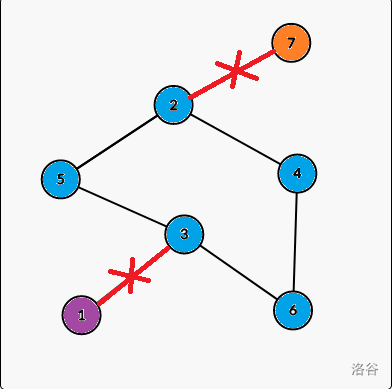
We can solve the problem like this because in each E-DCC there is no bridges.
// code of finding E-DCC
void dfs(int node, int ndcc)
{
dcc[node] = ndcc;
Ans[ndcc - 1].push_back(node);
for (int i = head[node]; i; i = e[i].nxt)
{
int to = e[i].to;
if (dcc[to] || b[i]) continue;
dfs(to, ndcc);
}
}






