Definiation : What is SCC
"SCC" means "strongly connected components.
In a directed graph , the nodes in the same SCC can visit each other.
In an easy way of understanding, if node $$$x$$$ and node $$$y$$$ are in the same SCC, there is a path from $$$x$$$ to $$$y$$$ and a path from $$$y$$$ to $$$x$$$.
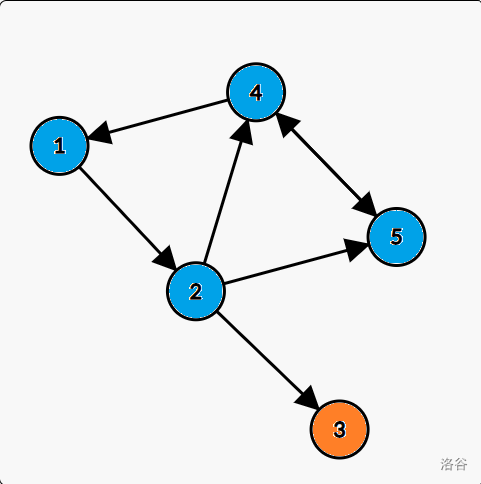
For example, in this graph, nodes in same color are in the same SCC:
Tarjan
Tarjan is one of the algorithms which can solve this problems.
First I am going to introduce two arrays to you:
$$$low_x$$$: An array of trace values representing the minimum idx of points on a search tree rooted at $$$x$$$ which can be reached by only one edge which is not in the search tree.
$$$dfn_x$$$: Timestamp array, representing the order it was visited.
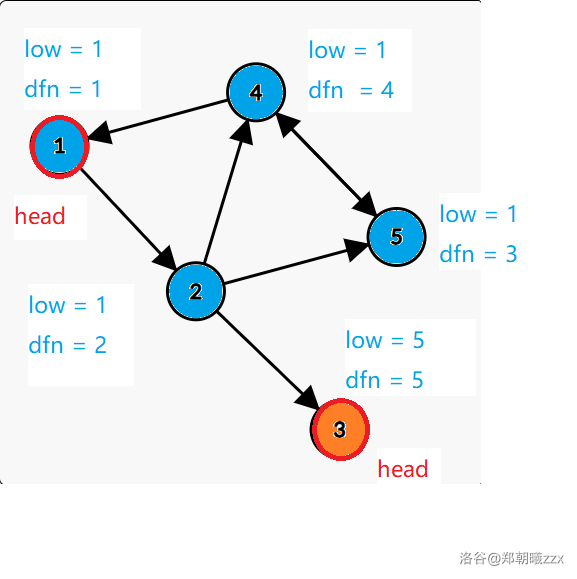
For example we can get the two values of the nodes:
How to calculate $$$low_x$$$?
We assume that there is an undirected edge from the node $$$x$$$ to the node $$$y$$$. There are two conditions:
- First: If node $$$y$$$ is a node of the subtree of node $$$x$$$, so
low[x] = min(low[x], low[y]); - Secound: Else
low[x] = min(low[x], dfn[y]);
Node that: In the secound condition, it is $$$dfn_y$$$, and it isn't $$$low_y$$$.
We should look back to the defination:
by only one edge which is not in the search tree
Only one edge!
How to find SCC base on $$$low$$$ and $$$dfn$$$?
Lets look back to the sample:

We can find that in each SCC there is a "head" which $$$low_x = dfn_x$$$. In this graph, the "heads" are node $$$1$$$ and node $$$3$$$.
We can use a stack to put the nodes we visited. When we get a "head", we should pop the elements in the stack and put them in the same SCC.
Lets read the sample together:
| node we meet | nodes in the stack | "head" | SCC |
|---|---|---|---|
| $$$1$$$ | $$$1$$$ | ||
| $$$2$$$ | $$$1\ 2$$$ | ||
| $$$5$$$ | $$$1 \ 2 \ 5$$$ | ||
| $$$4$$$ | $$$1 \ 2 \ 5 \ 4$$$ | There is an edge from $$$4$$$ to $$$1$$$, and we find a "head" node $$$1$$$ | |
| pop the stack | $$$empty$$$ | $$$1 \ 2 \ 5 \ 4$$$ | |
| $$$3$$$ | $$$3$$$ | $$$low_3 = dfn_3 = 5$$$, so node $$$3$$$ is a "head" | |
| pop the stack | $$$empty$$$ | $$$1 \ 2 \ 5 \ 4 \ and \ 3$$$ |
In this way, we can find the SCCs.
code in c++
void tarjan(int node)
{
printf("%d ", node);
stack[top++] = node;
low[node] = dfn[node] = ++id;
for (int i = head[node]; i; i = e[i].nxt)
{
int to = e[i].to;
if (dfn[to] == 0)
{
tarjan(to);
low[node] = min(low[node], low[to]);
}
else if (scc[to] == 0)
low[node] = min(low[node], dfn[to]);
}
if (low[node] == dfn[node])
{
++color_cnt;
ans.push_back(vector <int>());
while (true)
{
int to = stack[--top];
ans[color_cnt-1].push_back(to);
scc[to] = color_cnt;
if (node == to) break;
}
}
}
Recommend : More about connected components
If you want to learn more about connected components, can can read this aritical : A brief introduction of Tarjan and E-DCC(EBC).






