The algorithm of Tarjan is used to solve some problems which is about the connectedness of the Graph. Today I am going to introduce the key to solving E-DCC by Tarjan.
This problem is the template of V-DCC.
Defination : What is V-DCC?
The full name of E-DCC is vertex double connectivity component.
An E-DCC is a component that you cut any one of the vertexs, the graph is still connected.
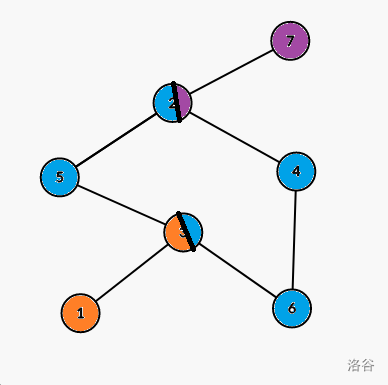
For example, in this graph, nodes in same color are in the same V-DCC, and there are $$$3$$$ V-DCCs in this graph. They are:
node 1, 3
node 2, 3, 4, 5, 6
node 2, 7
Solution : How to find V-DCC by Tarjan?
Cut vertex
First, we should know what "cut vertex" is. A "cut vertex" is a vertex in the graph, and if you cut the vertex off, the graph is not connected.
Tarjan
Tarjan is one of the algorithms which can solve this problems.
low and dfn
First I am going to introduce two arrays to you:
$$$low_x$$$: An array of trace values representing the minimum idx of points on a search tree rooted at x which can be reached by only one edge which is not in the search tree.
$$$dfn_x$$$: Timestamp array, representing the order it was visited.
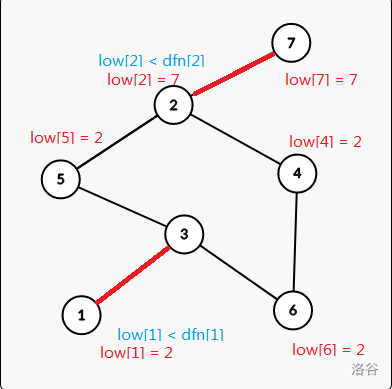
For example we can get the two values of the nodes:
How to calculate $$$low_x$$$?
We assume that there is an undirected edge from the node $$$x$$$ to the node $$$y$$$. There are two conditions:
- First: If node $$$y$$$ is a node of the subtree of node $$$x$$$, so
low[x] = min(low[x], low[y]); - Secound: Else
low[x] = min(low[x], dfn[y]);
Node that: In the secound condition, it is $$$dfn_y$$$, and it isn't $$$low_y$$$.
We should look back to the defination:
by only one edge which is not in the search tree
Only one edge!
How to find "cut vertex"
If a vertex $$$x$$$ is a cut vertex, if and only if $$$dfn_x \le low_y$$$.**
Note that this is not as same as "Bridge".
Lets look back to the example:

For node $$$2$$$, $$$low_2 = 7$$$ and $$$dfn_2 \le low_2$$$, so it is a cut vertex, because if node $$$2$$$ is cut, there isn't a path to connect node $$$7$$$.
Code of finding "cut vertex":
// note that "root" means "father"
void tarjan(int node, int root)
{
int scnt = 0;
dfn[node] = low[node] = ++num;
for (int i = head[node]; i; i = e[i].next)
{
const int to = e[i].to;
if (dfn[to] == 0)
{
++scnt;
fa[to] = node;
tarjan(to, root);
low[node] = min(low[node], low[to]);
if (low[to] >= dfn[node] && node != root) cut[node] = 1;
}
else if (to != fa[node])
low[node] = min(low[node], dfn[to]);
}
if (scnt >= 2 && node == root)
cut[root] = 1;
}
How to get V-DCC?
We can find that some vertexs are in more than one V-DCC. They are "cut vertex".
In any V-DCC, there are vertexs on the "border" of it, but not in the center. This is because if a cut vertex is in the center, we cut it, the connected component will break into two, but a cut vertex on the border of the V-DCC can be allowed, because when the vertex is cut, one of the new connected component is "empty", and the V-DCC will not break into two.
Because of this, we can set up a stack. When we visit a new vertex, we put it into the stack. When we find a "cut vertex", we should pop the elements in the stack until the cut vertex become the top of the stack. We shouldn't pop the "cut vertex", because the cut vertex is in more that one V-DCC.
Code of V-DCC:
void tarjan(int node)
{
dfn[node] = low[node] = ++id;
st[++top] = node;
if (node == root && head[node] == 0)
{
dcc[++sum].push_back(node);
return;
}
for (int i = head[node]; i; i = e[i].nxt)
{
int to = e[i].to;
if (dfn[to] == 0)
{
tarjan(to);
low[node] = min(low[node], low[to]);
if (low[to] >= dfn[node])
{
++sum;
int tmp;
while (1)
{
tmp = st[top--];
dcc[sum].push_back(tmp);
if (tmp == to) break;
}
dcc[sum].push_back(node);
}
}
else low[node] = min(low[node], dfn[to]);
}
}






