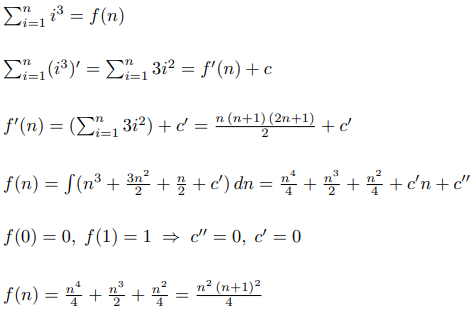Suppose you want to know this sum for some n and k:

Here are the well known formulas for the first several k:
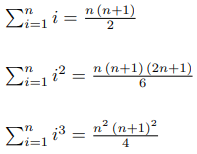
But suppose you forgot them. What to do? Luckily, there is an easy algorithm to generate those formulas.
First of all, let's prove a theorem.
Theorem
Suppose for every integer non-negative n:
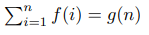
where f and g are polynoms. Then for some constant c:
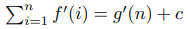
Proof
For every positive integer n:
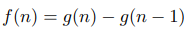
These two polynoms are equal in an infinite number of points, which means that they are identical. Which allows us to say:
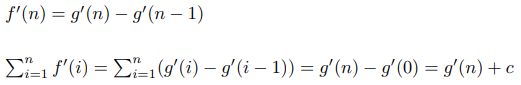
Application
Let's say we want to find the formula for the sum of squares. Then using our theorem we can create such an algorithm:
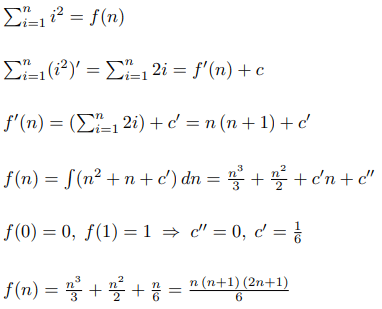
Now let's run the same algorithm to find the formula for the sum of cubes: