Div.2 A (Author: Haghani)
Idea is a simple greedy, buy needed meat for i - th day when it's cheapest among days 1, 2, ..., n.
So, the pseudo code below will work:
ans = 0
price = infinity
for i = 1 to n
price = min(price, p[i])
ans += price * a[i]

Time complexity: 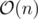
Div.2 B (Author: PrinceOfPersia)
Find all prime divisors of n. Assume they are p1, p2, ..., pk (in 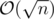 ). If answer is a, then we know that for each 1 ≤ i ≤ k, obviously a is not divisible by pi2 (and all greater powers of pi). So a ≤ p1 × p2 × ... × pk. And we know that p1 × p2 × ... × pk is itself lovely. So,answer is p1 × p2 × ... × pk
). If answer is a, then we know that for each 1 ≤ i ≤ k, obviously a is not divisible by pi2 (and all greater powers of pi). So a ≤ p1 × p2 × ... × pk. And we know that p1 × p2 × ... × pk is itself lovely. So,answer is p1 × p2 × ... × pk

Time complexity: 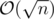
A (Author: PrinceOfPersia)
Problem is: you have to find the minimum number of k, such there is a sequence a1, a2, ..., ak with condition 2a1 + 2a2 + ... + 2ak = S = 2w1 + 2w2 + ... + 2w2. Obviously, minimum value of k is the number of set bits in binary representation of S (proof is easy, you can prove it as a practice :P).

Our only problem is how to count the number of set bits in binary representation of S? Building the binary representation of S as an array in 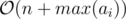 is easy:
is easy:
MAXN = 1000000 + log(1000000)
bit[0..MAXN] = {} // all equal to zero
ans = 0
for i = 1 to n
bit[w[i]] ++ // of course after this, some bits maybe greater than 1, we'll fix them below
for i = 0 to MAXN - 1
bit[i + 1] += bit[i]/2 // floor(bit[i]/2)
bit[i] %= 2 // bit[i] = bit[i] modulo 2
ans += bit[i] // if bit[i] = 0, then answer doesn't change, otherwise it'll increase by 1
Time complexity: 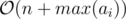
B (Author: PrinceOfPersia)
If we fix x and bix mod n, then problem will be solved (because we can then multiply it by the number of valid distinct values of 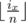 ).
).
For the problem above, let dp[i][j] be the number of valid subsequences of b where x = j and 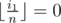 and
and 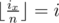 . Of course, for every i, dp[i][1] = 1. For calculating value of dp[i][j]:
. Of course, for every i, dp[i][1] = 1. For calculating value of dp[i][j]:
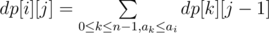
For this purpose, we can sort the array a and use two pointer:
if p0, p1, ...pn - 1 is a permutation of 0, ..., n - 1 where for each 0 ≤ t < n - 1, apt ≤ apt + 1:
for i = 0 to n-1
dp[i][1] = 1
for j = 2 to k
pointer = 0
sum = 0
for i = 0 to n-1
while pointer < n and a[p[pointer]] <= a[i]
sum = (sum + dp[p[pointer ++]][j - 1]) % MOD
dp[i][j] = sum

Now, if 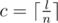 and x = l - 1 mod n, then answer equals to
and x = l - 1 mod n, then answer equals to 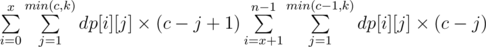 (there are c - j + 1 valid different values of
(there are c - j + 1 valid different values of 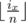 for the first group and c - j for the second group).
for the first group and c - j for the second group).
Time complexity: 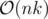
C (Author: PrinceOfPersia)
Solution is something like the fourth LCA approach discussed here.
For each 1 ≤ i ≤ n and 0 ≤ j ≤ lg(n), store the minimum 10 people in the path from city (vertex) i to its 2j - th parent in an array.
Now everything is needed is: how to merge the array of two paths? You can keep the these 10 values in the array in increasing order and for merging, use merge function which will work in 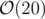 . And then delete the extra values (more than 10).
. And then delete the extra values (more than 10).
And do the same as described in the article for a query (just like the preprocess part).

Time complexity: 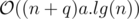
D (Author: PrinceOfPersia)
Run binary search on the answer (t). For checking if answer is less than or equal to x (check(x)):
First of all delete all edges with destructing time greater than x. Now, if there is more than one pair of edges with the same color connected to a vertex(because we can delete at most one of them), answer is "No".
Use 2-Sat. Consider a literal for each edge e (xe). If xe = TRUE, it means it should be destructed and it shouldn't otherwise. There are some conditions:
For each vertex v, if there is one (exactly one) pair of edges like i and j with the same color connected to v, then we should have the clause
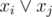 .
.For each vertex v, if the edges connected to it are e1, e2, ..., ek, we should make sure that there is no pair (i, j) where 1 ≤ i < j ≤ k and xe1 = xe2 = True. The naive approach is to add a clause
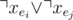 for each pair. But it's not efficient.
for each pair. But it's not efficient.

The efficient way tho satisfy the second condition is to use prefix or: adding k new literals p1, p2, ..., pk and for each j ≤ i, make sure 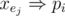 . To make sure about this, we can add two clauses for each pi:
. To make sure about this, we can add two clauses for each pi: 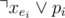 and
and 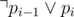 (the second one is only for i > 1).
(the second one is only for i > 1).
And the only thing left is to make sure 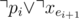 (there are no two
(there are no two TRUE edges).
This way the number of literals and clauses are 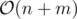 .
.
So, after binary search is over, we should run check(t) to get a sample matching.
Time complexity: 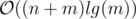 (but slow, because of the constant factor)
(but slow, because of the constant factor)
E (Authors: PrinceOfPersia and Haghani)
Lemma #1: If numbers b1, b2, ..., bk are k Kheshtaks of a1, ..., an, then  is a Kheshtak of a1, ..., an.
is a Kheshtak of a1, ..., an.
Proof: For each 1 ≤ i ≤ k, consider maski is a binary bitmask of length n and its j - th bit shows a subsequence of a1, ..., an (subset) with xor equal to bi.
So, xor of elements subsequence(subset) of a1, ..., an with bitmask equal to 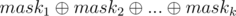 equals to
equals to  . So, it's a Kheshtak of this sequence.
. So, it's a Kheshtak of this sequence.
From this lemma, we can get another results: If all numbers b1, b2, ..., bk are k Kheshtaks of a1, ..., an, then every Kheshtak of b1, b2, ..., bk is a Kheshtak of a1, ..., an
Lemma #2: Score of sequence a1, a2, ..., an is equal to the score of sequence 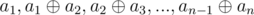 .
.
Proof: If we show the second sequence by b1, b2, ..., bn, then for each 1 ≤ i ≤ n:
- bi =
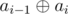
- ai =

 each element from sequence b is a Kheshtak of sequence a and vise versa. So, due to the result of Lemma #1, each Kheshtak of sequence b is a Kheshtak of sequence a and vise versa. So:
each element from sequence b is a Kheshtak of sequence a and vise versa. So, due to the result of Lemma #1, each Kheshtak of sequence b is a Kheshtak of sequence a and vise versa. So:
- score(b1, ..., bn) ≤ score(a1, ..., an)
- score(a1, ..., an) ≤ score(b1, ..., bn)
 score(a1, ..., an) = score(b1, ..., bn)
score(a1, ..., an) = score(b1, ..., bn)

Back to original problem: denote another array b2, ..., bn where 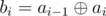 . Let's solve these two problems:
. Let's solve these two problems:
1- We have array a1, ..., an and q queries of two types:
- upd(l, r, k): Given numbers l, r and k, for each l ≤ i ≤ r, perform
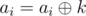
- ask(i): Given number i, return the value of ai.
This problem can be solved easily with a simple segment tree using lazy propagation.
2- We have array b2, ..., bn and queries of two types:
- modify(p, k): Perform bp = k.
- basis(l, r): Find and return the basis vector of bl, bl + 1, ..., br (using Gaussian Elimination, its size it at most 32).
This problem can be solved by a segment tree where in each node we have the basis of the substring of that node (node [l, r) has the basis of sequence bl, ..., br - 1).
This way we can insert to a basis vector v:
insert(x, v)
for a in v
if a & -a & x
x ^= a
if !x
return
for a in v
if x & -x & a
a ^= x
v.push(x)
But size of v will always be less than or equal to 32. For merging two nodes (of segment tree), we can insert the elements of one in another one.
For handling queries of two types, we act like this:
Type one: Call functions: upd(l, r, k), 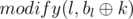 and
and 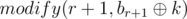 .
.
Type two: Let b = basis(l + 1, r). Call insert(al, b). And then print 2b.size() as the answer.
Time complexity: 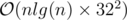 =
= 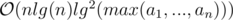
F (Author: PrinceOfPersia)
Use Aho-Corasick. Assume first of all we build the trie of our strings (function t). If t(v, c) ≠ - 1 it means that there is an edge in the trie outgoing from vertex v written c on it.
So, for building Aho-Corasick, consider f(v) = the vertex we go into, in case of failure (t(v, c) = - 1). i.e the deepest vertex (u), that v ≠ u and the path from root to u is a suffix of path from root to v. No we can build an automaton (Aho-Corasick), function g. For each i, do this (in the automaton):
cur = root
for c in s[i]
cur = g(cur, c)
And then push i in q[cur] (q is a vector, also we do this for cur = root).
end[cur].push(i) // end is also a vector, consisting of the indices of strings ending in vertex cur (state cur in automaton)
last[i] = cur // last[i] is the final state we get to from searching string s[i] in automaton g
Assume cnt(v, i) is the number of occurrences of number i in q[v]. Also, denote 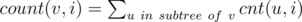 .
.
Build another tree. In this tree, for each i that is not root of the trie, let par[i] = f(i) (the vertex we go in the trie, in case of failure) and call it C-Tree.
So now, problem is on a tree. Operations are : Each query gives numbers l, r, k and you have to find the number 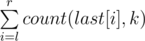 .
.

Act offline. If N = 105, then:
1. For each i such that 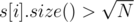 , collect queries (like struct) in a vector of queries query[i], then run
, collect queries (like struct) in a vector of queries query[i], then run dfs on the C-Tree and using a partial sum answer to all queries with k = i. There are at most  of these numbers, so it can be done in
of these numbers, so it can be done in 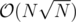 . After doing these, erase i from all q[1], q[1], ..., q[N].
. After doing these, erase i from all q[1], q[1], ..., q[N].
Code (in dfs) would be like this(on C-Tree):
partial_sum[n] = {}; // all 0
dfs(v, i){
cnt = 0;
for x in q[v]
if(x == i)
++ cnt;
for u in childern[v]
cnt += dfs(u);
for x in end[v]
partial_sum[x] += cnt;
return cnt;
}
calc(i){
dfs(root, i);
for i = 2 to n
partial_sum[i] += partial_sum[i-1]
for query u in query[i]
u.ans = partial_sum[u.r] - partial_sum[u.l - 1]
}
And we should just run calc(i) for each of them.
2. For each i such that 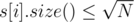 , collect queries (like struct) in a vector of queries query[i]. (each element of this vector have three integers in it: l, r and ans).
, collect queries (like struct) in a vector of queries query[i]. (each element of this vector have three integers in it: l, r and ans).
Consider this problem:
We have an array a of length N(initially all element equal to 0) and some queries of two types:
- increase(i, val): increase a[i] by val
- sum(i): tell the value of a[1] + a[2] + ... + a[i]
We know that number of queries of the first type is 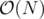 and from the second type is
and from the second type is 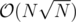 . Using Sqrt decomposition, we can solve this problem in
. Using Sqrt decomposition, we can solve this problem in 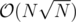 :
:
K = sqrt(N)
tot[K] = {}, a[N] = {} // this code is 0-based
increase(i, val)
while i < N and i % K > 0
a[i ++] += val
while i < K
tot[i/K] += val
i += K
sum(i)
return a[i] + tot[i/K]
Back to our problem now.
Then, just run dfs once on this C-Tree and act like this:
dfs(vertex v):
for i in end[v]
increase(i, 1)
for i in q[v]
for query u in query[i]
u.ans += sum(u.r) - sum(u.l - 1)
for u in children[v]
dfs(u)
for i in end[v]
increase(i, -1)
Then answer to a query q is q.ans.
Time complexity: