Yeah, yeah, I know you expect from me matrix jokes. What if I told you I have no jokes on that ? So, just take the blue pill and go into serious stuff like ...
Cutting to the chase
I personally find matrix multiplication as the guy who sells stolen phones at the corner of the street. I mean, you get stuff at lower price but it can break in two days and you can get busted by the cops. Or not. I really need to find better metaphors...
Matrix multiplication is a well known method. People wrote on it before quite good articles, but I think you might get stuff simpler just by looking over some problems. For the ones who are familiar with the topic, you can skip to the last two problems.
Getting high fast
Now I need to find better subtitles... However, first of all to know logarithmic matrix multiplication, you have to know logarithmic multiplication.
Basically we have to compute xn considering the multiplication operation take O(1) time. Take it straight forward we get xn = x * x * .. * x , so O(N). Let's try to reduce it step by step. Let's take xn = x2 * x2 * .... And we multiply by x if n is odd. This should work fine and the constant is reduced at half. Right... Similarly we can go to xn = xsqrt(n) * xsqrt(n) * ... and this goes to O(sqrtN). This reasoning stops here.
To get it faster you have to simply observe that xn = xn / 2 * xn / 2 for n even and xn = xn / 2 * xn / 2 * x for n odd. The two terms are the same and the third is constant, so we really need to compute xn / 2 once. And xn / 4 once. And so on. Therefore the O(logN) complexity.
Now, notice that we did not specified that x is an integer or a number. The same rules hold for other mathematical associative structures such as matrices.
Don't get stuck with struct
If you sayin' Y U NO REMEMBER MATRIX, then let me refresh your maths knowledge. You don't really need to know much about matrices to use put recurrences in a matrix multiplication form. Multiplying squared matrices is straight forward. Given two matrices their product is
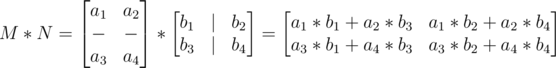
Each element in each row in M is multiplied by its correspondent in the columns of N. If you find it simpler to remember, just imagine horizontal rows splitting matrix M and vertical row splitting matrix N and then match each row with each column.
Let's make a structure in which we keep a matrix. If new to matrices you should get an idea how matrix multiplication works from the code below.
struct matrix {
// N is the size of the matrix
int m[N][N];
matrix()
{
memset(m,0,sizeof(m));
}
matrix operator * (matrix b)
{
matrix c = matrix();
for (int i = 0; i < N; ++i)
for (int j = 0; j < N; ++j)
for (int k = 0; k < N; ++k)
c.m[i][j] = (c.m[i][j] + 1LL * m[i][k] * b.m[k][j]) % M;
return c;
}
...
};
Notice that we define the multiplication operation. We specifically did this so we can use a matrix exactly as a number in the logarithmic multiplication algorithm. So the code will be the same for an int and a matrix. Pretty cool if I do say so. And I do.
matrix modPow(matrix m,int n)
{
if ( n == 0 )
return unit; // the unit matrix - that is 1 for principal diagonal , otherwise 0
matrix half = modPow(m,n/2);
matrix out = half * half;
if ( n % 2 )
out = out * x;
return out;
}
Note that we could have defined an operator for power multiplication or used a template that we could have applied for a general type, but I find the implementation above more clear due to the clarity of the recurrence.
N-th Fibonacci term
For starters, let's define:
Fn = Fn - 1 + Fn - 2 with F1 = 1, F2 = 1
We need to put this in the form of a matrix recurrence. Well, each term is dependent of other consecutive two. This is a good clue we need just a 2 row matrix. So, from Fn - 2 and Fn - 1 we need to compute Fn. To keep the recurrences squared we will compute from the pair (Fn - 2, Fn - 1) the pair (Fn - 1, Fn).
Fn = Fn - 1 * 1 + Fn - 2 * 1 Fn - 1 = Fn - 1 * 1 + Fn - 2 * 0
Or, as matrices:

Going one step backwards we got:

Finally:
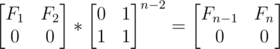
Getting  at power n takes logarithmic time , so that is just... fast.
at power n takes logarithmic time , so that is just... fast.
Bits and pieces
As you can see, this technique can be used to calculate the n-th term of a linear recurrence. In the following example we need to find out how many arrays of length n with maximum k consecutive 0 bits are there. ( n ≤ 109, k ≤ 40 )
Let's suppose n is small enough so we can use dynamic programming to solve the problem. Denote Dn, k = number of arrays of length n which end in k number of 0s
As you can guess one can make two moves: add a 0 and add a 1. Therefore, from state (n, k) we can go to states (n + 1, k + 1) and (n + 1, 0). So 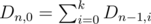 and Dn, k = Dn - 1, k. As we did before, let's write down all recurrences we are interested in.
and Dn, k = Dn - 1, k. As we did before, let's write down all recurrences we are interested in.
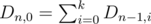
Dn, 1 = Dn - 1, 0
Dn, 2 = Dn - 1, 1
...
Dn, k = Dn - 1, k
The matrix recurrence will come straight away:

As you can see, now the complexity of the solution is reduces from O(N * K) to O(logN * K3), the K3 being the complexity of multiplying 2 K-size matrices.
How big can it get ?
Now seriously, I really need better subtitles. Problem (Chimney)[http://community.topcoder.com/stat?c=problem_statement&pm=11512&rd=14546] from TopCoder can be solved similarly with the problems above.
Usually, when we got a big N, this is a hint in favor of logarithmic multiplication. So we have to find a recurrence. More specifically, we have to find a good way to represent a state.
You can also note that we are not really interested how many layers have been completed, but what are the last moves made. So we can have the next forms of completed blocks in the last layer:
+-----+--+ +-----+--+ +-----+--+ +-----+--+ +-----+--+ +-----+--+ +-----+--+ +-----+--+
| 0 | | | 0 | | | 0 | | | 0 | |
+--+--|0 |
| | | |
| 0+--+--+
| | 0 |
+--+-----+





