Let's fix the number a of strings of length p and the number b of strings of length q. If a·p + b·q = n, we can build the answer by splitting the string s to a parts of the length p and b parts of the length q, in order from left to right. If we can't find any good pair a, b then the answer doesn't exist. Of course this problem can be solved in linear time, but the constraints are small, so you don't need linear solution.
Complexity: O(n2).
612B - HDD is Outdated Technology
You are given the permutation f. Let's build another permutation p in the following way: pfi = i. So the permutation p defines the number of sector by the number of fragment. The permutation p is called inverse permutation to f and denoted f - 1. Now the answer to problem is 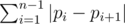 .
.
Complexity: O(n).
612C - Replace To Make Regular Bracket Sequence
If we forget about bracket kinds the string s should be RBS, otherwise the answer doesn't exist. If the answer exists each opening bracket matches to exactly one closing bracket and vice verse. Easy to see that if two matching brackets have the same kind we don't need to replace them. In other case we can change the kind of the closing bracket to the kind of the opening. So we can build some answer. Obviously the answer is minimal, because the problems for some pair of matching pairs are independent and can be solved separately.
The only technical problem is to find the matching pairs. To do that we should store the stack of opening brackets. Let's iterate from left to right in s and if the bracket is opening, we would simply add it to the stack. Now if the bracket is closing there are three cases: 1) the stack is empty; 2) at the top of the stack is the opening bracket with the same kind as the current closing; 3) the kind of the opening bracket differs from the kind of the closing bracket. In the first case answer doesn't exist, in the second case we should simply remove the opening bracket from the stack and in the third case we should remove the opening bracket from the stack and increase the answer by one.
Complexity: O(n).
612D - The Union of k-Segments
Let's create two events for each segment li is the time of the segment opening and ri is the time of the segment closing. Let's sort all events by time, if the times are equal let's sort them with priority to opening events. In C++ it can be done with sorting by standard comparator of vector<pair<int, int>> events, where each element of events is the pair with event time and event type ( - 1 for opening and + 1 for closing).
Let's iterate over events and maintain the balance. To do that we should simply decrease the balance by the value of the event type. Now if the balance value equals to k and before updating it was k - 1 then we are in the left end of some segment from the answer. If the balance equals to k - 1 and before updating it was k then we are in the right end of the segment from the answer. Let's simply add segment [left, right] to the answer. So now we have disjoint set of segments contains all satisfied points in order from left to right. Obviously it's the answer to the problem.
Complexity: O(nlogn).
612E - Square Root of Permutation
Consider some permutation q. Let's build by it the oriented graph with edges (i, qi). Easy to see (and easy to prove) that this graph is the set of disjoint cycles. Now let's see what would be with that graph when the permutation will be multiplied by itself: all the cycles of odd length would remain so (only the order of vertices will change, they will be alternated), but the cycles of even length will be split to the two cycles of the same length. So to get the square root from the permutation we should simply alternate (in reverse order) all cycles of the odd length, and group all the cycles of the same even length to pairs and merge cycles in each pair. If it's impossible to group all even cycles to pairs then the answer doesn't exist.
Complexity: O(n).
The author solution for this problem uses dynamic programming. I think that this problem can't be solved by greedy ideas. Let's calculate two dp's: z1i is the answer to the problem if all numbers less than ai are already printed, but the others are not; and z2i is the answer to the problem if all numbers less than or equal to ai are already printed, but the others are not. Let's denote dij — the least distance between i and j on the circular array and odij is the distance from i to j in clockwise order. Easy to see that z2i = minj(zj + dij) for all j such that the value aj is the least value greater than ai. Now let's calculate the value z1i. Consider all elements equals to ai (in one of them we are). If there is only one such element then z1i = z2i. Otherwise we have two alternatives: to move in clockwise or counterclockwise direction. Let we are moving in clockwise direction, the last element from which we will write out the number would be the nearest to the i element in counterclockwise direction, let's denote it u. Otherwise at last we will write out the number from the nearest to the i element in clockwise direction, let's denote it v. Now z1i = min(z2u + odiu, z2v + odvi). Easy to see that the answer to the problem is mini(z1i + dsi), over all i such that ai is the smallest value in array and s is the start position.
Additionally you should restore the answer. To do that, on my mind, the simplest way is to write the recursive realization of dp, test it carefully and then copy it to restore answer (see my code below). Of course, it's possible to restore the answer without copy-paste. For example, you can add to your dp parameter b which means it's need to restore answer or not.
Complexity: O(n2).







