Seriously, why so serious? And why so mainstream? Competitive programming is all about fun, therefore...
Cutting to the chase
I'll talk about something that goes like that: everyone talks about it, few really know how to do it, everyone thinks everybody else knows how to do it, so everyone claims they know how to do it.Not teenage sex, but understanding data structures. In the sense of the metaphor before, I am close to a virgin but I still can give you some insight as there are some structures that are my type. I will write more on data structures, but this time we'll look at tries.
Don't get me wrong, I am talking about data structure that tend to be implemented and modeled the same way each time due to habit or even not implemented(cause STL has them).
Note that I will put more emphasis on the steps in getting the solution than on the implementation and the way the data structure works, because there are many great articles on it. ### The good ol' dictionary
We'll try to implement a structure that can handle the following queries:
- add(w) — add an apparition of word w in the data structure
- remove(w) — delete an apparition of word w in the data structure
- find(w) — get the number of apparition of word w in the list
- count(w) — get the number of words from the data structure that have the longest common prefix with word w
Let's ignore the 4th type of query.
Now what's the simplest way to do this? Keep a list an loop through it. Nothing wrong with that, but we need faster stuff. The obvious thing that a programmer would think at is giving the words some order so that the search is faster. This is exactly what STL's unordered_map does. So a map would to the business. Supposing you want to implement it yourself, you should find a nice hashing function the problem might be solved. OK, I'll go home, we're done.
Give it a trie
At this moment we have a decent data structure but we did not solved the 4th query. Also, we did not use one information: we are working with strings. Now we need some observation to go on: if some strings have a common prefix, the prefix should be stored only once and we would need to somehow point to more places from that position.
Now the observation, even if pertinent, does not give any simplification because we are talking about prefixes, so chunks of strings. A simple man, like me, would start with baby steps.
For starters, we'll make from each letter a node and we will bound it to the next word in the string. Suppose we introduced words "awesome" and "awful".
[a] -> [w] -> [e] -> [s] -> [o] -> [m] -> [e]
[a] -> [w] -> [f] -> [u] -> [l]
Now put the common prefix together and we have:
[a] -> [w] -> [e] -> [s] -> [o] -> [m] -> [e]
-> [f] -> [u] -> [l]
That tree structure looks quite nice, because if we will have something like that and a nice method of accessing each element we could solve this in something close to O(length * accessing) where O(accessing) is the time of the access method we choose.
Let's choose how we store data and access it. Store a root node that has no character in it — this will be the start point in the tree. Say we have only 26 chars, then we can keep a vector of pointers and the current char in each node. That's how our model looks now:
The complexities are O(length) for each operation due to the, but the memory is quite big as it can go to maximum O(totalLength * SIGMA) where SIGMA is the total number of chars. To insert, delete and find operations will be straight forward: go and access stuff if you can, if the string ends just modify the tree. The count will be something similar but we need to compute the size of each subtree at each step, and return that value each time we arrive at the longest common prefix.
At this point you can take a brake, cry cause you don't understand and then return and try to look at the next code:
struct trie
{
int v,sz;
trie *sons[26];
trie()
{
v = sz = 0;
memset(sons,0,sizeof(sons));
}
int find(char* c)
{
if ( *c == 0 )
return v;
if ( sons[int(*c)-int('a')] != NULL )
return sons[int(*c)-int('a')]->find(c+1);
else
return 0;
}
void add(char *c)
{
if ( *c == 0 )
{
v++;
sz++;
return;
}
if ( sons[int(*c)-int('a')] == NULL )
sons[int(*c)-int('a')] = new trie();
sz -= sons[int(*c)-int('a')]->sz;
sons[int(*c)-int('a')]->add(c+1);
sz += sons[int(*c)-int('a')]->sz;
}
void remove(char *c)
{
if ( *c == 0 )
{
v--;
sz--;
return;
}
if ( sons[int(*c)-int('a')]->sz == 0 )
sons[int(*c)-int('a')] = new trie();
else
{
sz -= sons[int(*c)-int('a')]->sz;
sons[int(*c)-int('a')]->remove(c+1);
sz += sons[int(*c)-int('a')]->sz;
if ( sons[int(*c)-int('a')]->sz == 0 )
sons[int(*c)-int('a')] = NULL;
}
}
int count(char *c,int now)
{
if ( *c == 0 )
return now;
if ( sons[int(*c)-int('a')] != NULL )
return sons[int(*c)-int('a')]->count(c+1,now+1);
else
return now;
}
};
To reduce the memory in case of a big SIGMA we can store maps/unordered_map in each node, but this will give a slower solution, still a nicer one.
Trie different
Now, how a map works? Is some kind of a binary search tree. So why not embed such a structure in the trie in the first place?
People, ternary search tree. Ternary search tree, people. Now let's get to know this guy in more detail.
We construct the node different this time based on the actions that can happen at a moment when we, let's say insert something. There are 3 scenarios when we are in a node that stores a char c and at the s character of the string:
- s > c
- s < c
- s = c
We will stick out 3 edges from each node for each scenario and we stop when s points to a null position. Our life is much easier like this, but what are the times supported by this structure.
In worst case you will do a slalom between smaller or bigger chars. Therefore each operation will have a worst time case of O(SIGMA * length), but in average the structure will give a complexity of O(length * log(SIGMA)). The demonstration gives some intuition into the way a binary search tree works on average inputs.
For some schematic representation you can imagine something like that:
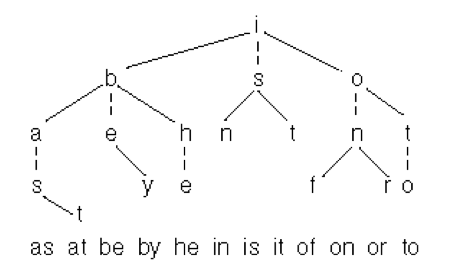
Summing up
- I do very bad intros.
- With a healthy approach that forms with exercise, we can get to solve this kind of problems.
- A problem can be solved in many different ways and data structures teach us that at each occasion.
- Both "classic" tries and TSTs are cool.
- Now I also do very bad endings.
Question
Can you think of something similar to the TST but with better worst times?
PS
Thank you for reading and please state your opinion on my tutorial. (or, more specifically, on my writing style and how useful you find the material presented) Any suggestions for next tutorial are welcome.
You can find my previous article here.
Hope you enjoyed!





