628A - Tennis Tournament
The problem was suggested by unprost.
Here you can simply model the process. Or you can note that after each match some player drops out. In total n - 1 players will drop out. So the first answer is (n - 1) * (2b + 1). Obviously the second answer is np.
Complexity: O(log2n), O(logn) or O(1) depends on the realization.
628B - New Skateboard
This is one of the problems suggested by Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.
The key observation is that the number is divisible by 4 if and only if its last two digits forms a number divisible by 4. So to calculate the answer at first we should count the substrings of length one. Now let's consider pairs of consecutive digits. If they forms a two digit number that is divisible by 4 we should increase the answer by the index of the right one.
Complexity: O(n).
628C - Bear and String Distance
The problem was suggested and prepared by Kamil Debowski Errichto. He also wrote the editorial.
There is no solution if the given required distance is too big. Let's think what is the maximum possible distance for the given string s. Or the more useful thing — how to construct a string s' to maximize the distance? We can treat each letter separately and replace it with the most distant letter. For example, we should replace 'c' with 'z', and we should replace 'y' with 'a'. To be more precise, for first 13 letters of the alphabet the most distant letter is 'z', and for other letters it is 'a'.
Let's solve a problem now. We can iterate over letters and greedily change them. A word "greedily" means when changing a letter we don't care about the next letters. We generally want to choose distant letters, because we may not find a solution otherwise. For each letter si we change it into the most distant letter, unless the total distance would be too big. As we change letters, we should decrease the remaining required distance. So, for each letter si consider only letters not exceeding the remaining distance, and among them choose the most distant one. If you don't see how to implement it, refer to my C++ solution with comments.
Complexity: O(n).
628D - Magic Numbers
Kareem Mohamed Kareem_Mohamed suggested the simpler version of the problem.
Denote the answer to the problem f(a, b). Note that f(a, b) = f(0, b) - f(0, a - 1) or what is the same f(a, b) = f(0, b) - f(0, a) + g(a), where g(a) equals to one if a is a magic number, otherwise g(a) equals to zero. Let's solve the problem for the segment [0, n].
Here is described the standard technique for this kind of problems, sometimes it is called 'dynamic programming by digits'. It can be realized in a two ways. The first way is to iterate over the length of the common prefix with number n. Next digit should be less than corresponding digit in n and other digits can be arbitrary. Below is the description of the second approach.
Let zijk be the number of magic prefixes of length i with remainder j modulo m. If k = 0 than the prefix should be less than the corresponding prefix in n and if k = 1 than the prefix should be equal to the prefix of n (it can not be greater). Let's do 'forward dynamic programming'. Let's iterate over digit 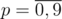 in position i. We should check that if the position is even than p should be equal to d, otherwise it cannot be equal to d. Also we should check for k = 1 p should be not greater than corresponding digit in n. Now let's see what will be the next state. Of course i' = i + 1. By Horner scheme j' = (10j + p) mod m. Easy to see that
in position i. We should check that if the position is even than p should be equal to d, otherwise it cannot be equal to d. Also we should check for k = 1 p should be not greater than corresponding digit in n. Now let's see what will be the next state. Of course i' = i + 1. By Horner scheme j' = (10j + p) mod m. Easy to see that 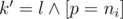 . To update the next state we should increase it: zi'j'k' + = zijk. Of course all calculations should be done modulo 109 + 7.
. To update the next state we should increase it: zi'j'k' + = zijk. Of course all calculations should be done modulo 109 + 7.
Complexity: O(nm).
628E - Zbazi in Zeydabad
The problem was suggested by Ali Ahmadi Kuzey.
Let's precalculate the values zlij, zrij, zldij — the maximal number of letters 'z' to the left, to the right and to the left-down from the position (i, j). It's easy to do in O(nm) time. Let's fix some cell (i, j). Consider the value c = min(zlij, zldij). It's the maximum size of the square with upper right ceil in (i, j). But the number of z-patterns can be less than c. Consider some cell (x, y) diagonally down-left from (i, j) on the distance no more than c. The cells (i, j) and (x, y) forms z-pattern if y + zrxy > j.
Let's maintain some data structure for each antidiagonal (it can be described by formula x + y) that can increment in a point and take the sum on a segment (Fenwick tree will be the best choice for that). Let's iterate over columns j from the right to the left and process the events: we have some cell (x, y) for which y + zrxy - 1 = j. In that case we should increment the position y in the tree number x + y by one. Now we should iterate over the cells (x, y) in the current column and add to the answer the value of the sum on the segment from j - c + 1 to j in the tree number i + j .
Complexity: O(nmlogm).
628F - Bear and Fair Set
The problem was suggested and prepared by Kamil Debowski Errichto. He also wrote the editorial.
At the beginning, to make things simpler, we should add a query (hint) with upTo = b, quantity = n, and then sort queries by upTo. Sorted queries (hints) divide interval [1, b] into q disjoint intervals. For each interval we know how many elements should be there.
Let's build a graph and find a max flow there. The answer is "YES" only if the flow is n.
- The first group A contains 5 vertices, representing possible remainders.
- The second group B contains q vertices, representing intervals.
Each vertex from A should be connected with the source by an edge with capacity n / 5. Each vertex from B should be connected with the sink by an edge with capacity equal to the size of the interval. Between each vertex x from A and y from B should be an edge with capacity equal to the number of numbers in the interval y, giving remainder x when divided by 5.
You can also use see that it's similar to finding matching. In fact, we can use the Hall's marriage theorem. For each of 25 sets of vertices from A (sets of remainders) iterate over intervals and count how many numbers we can take from [1, b] with remainders from the fixed set of remainders.
The implementation with the Hall's theorem: C++ solution.
Complexity: O(2Cn). In our problem C = 5.







