Hi guys!
On IOI I've learned many new things, so now I want to give you a challenge. You probably remember my and Errichto's eliminations to VK Cup 2016. Let's focus on this problem: 674C - Levels and Regions
Main solution was solving it in O(n*k), because k wasn't greater than 50. What if k is just lower or equal to n? :D
I'm posting solution below this text, if you want to read it just scroll down.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
SOLUTION ALERT
There are two key observations.
- Obviously, higher k means smaller result.
- For every i (1 < i < n) there is res(i + 1) - res(i) ≤ res(i) - res(r - 1).
The above implies that for every i (that 1 ≤ i ≤ n) there exists such real value X that res(i) + i·X ≤ res(j) + j·X for every 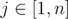 . Also, for fixed i good X's are between res(i + 1) - res(i) and res(i) - res(i - 1), inclusive (except for trivial cases k = 1 and k = n).
. Also, for fixed i good X's are between res(i + 1) - res(i) and res(i) - res(i - 1), inclusive (except for trivial cases k = 1 and k = n).
So, when we have fixed X, we can calculate the minimum value of dividing sequence into intervals (we can use any number of them), where cost for an interval is the same as in the basic version of task plus X. Using the convex hull trick, we can do it in O(n). Then we check how many intervals we've used to do it. If we've used too many, we know that X should be greater (to force the algorithm to use smaller number of intervals). If we've used at most k intervals, we should make X lower. So now we see that we should use binary search to find good X!
After finding good X, we just calculate the optimum value for full sequence and subtract k·X. This gives us O(n·log) solution.
SOLUTION ALERT






