Introduction
It's been around 18 months since this problem first crossed my way and yesterday I've finally understood the author's intended solution (thanks to thiagocarvp's patient explanation!). I think this solution is somehow explained here, but I also think it can be explained in a better way. This is the goal of this post.
Problem statement
First, you're given a connected graph with n vertices and m weighted edges. And then a sequence of q new edges is added to the graph. For each of these q new edges, output the weight of a minimum spanning tree considering only this and the previous edges. For example, take V = {1, 2}, E = {({1, 2}, 5)} and the sequence (({1, 2}, 7), ({1, 2}, 3)), i.e., n = 2, m = 1 and q = 2. The answers are 5 and 3, respectively.
Naive approach
Let's try to answer the queries online. First, build a MST for the initial graph. All we can do with new edges is try to improve the current MST, i.e., the MST can only become lighter, never heavier. It's not hard to see that the required procedure is the following greedy algorithm.
There are only two possibilities for a new edge ({u, v}, w):
- An edge between u and v is already present in the MST. In this case, just update its weight taking the minimum between the new and the old weight.
- There's no edge between u and v in the current MST. In this case, the new edge will create a cycle. Then just remove the heaviest edge from this cycle.
The first situation can be easily handled in 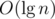 using maps. The second, however, takes more effort. A simple DFS could find and remove the heaviest edge of the cycle, but it would cost O(n) operations, resulting in a total running time of at least
using maps. The second, however, takes more effort. A simple DFS could find and remove the heaviest edge of the cycle, but it would cost O(n) operations, resulting in a total running time of at least 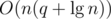 operations in the worst case. Alternatively, it's possible to augment a link cut tree to do all this work in
operations in the worst case. Alternatively, it's possible to augment a link cut tree to do all this work in 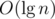 per new edge, resulting in a much better
per new edge, resulting in a much better 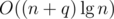 running time.
running time.
So the naive approach is either too slow (DFS), or too much code (link cut tree).
Author's intended solution
The naive approach might be hard to apply, but it certainly helps us to make an important observation:
Two consecutive MSTs will differ in at most one edge.
In other words, the changes in the solution are very small from one query to the next. And we are going to take advantage of this property, like many popular offline algorithms do. In particular, we'll do something like the square root decomposition of Mo's algorithm. Usually, this property is achieved by sorting the queries in a special way, like Mo's algorithm itself requires. In our case, we have just noticed that this is not necessary. Hence, we'll process the queries in a very straightforward way (and I keep asking myself what took me so long to understand this beautiful algorithm!).
The observation is used as follows. We'll split the queries in 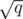 consecutive blocks of
consecutive blocks of 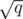 consecutive queries. If we compute the edges that simultaneously belong to all the MSTs of one block, we'll be able to reduce the size of the graph for which we should compute minimum spanning trees. In other words, we're going to run Kruskal's algorithm q times, once per new edge, but it will run for much smaller graphs. Let's see the details.
consecutive queries. If we compute the edges that simultaneously belong to all the MSTs of one block, we'll be able to reduce the size of the graph for which we should compute minimum spanning trees. In other words, we're going to run Kruskal's algorithm q times, once per new edge, but it will run for much smaller graphs. Let's see the details.
First, imagine the MST Ti computed right after adding the edge e of the i-th query. Now, if e belongs to Ti, consider  . What does it look like? Sure, Ti' is a forest with two trees (components). And if we condense these two components, we'll get a much smaller graph with precisely two vertices and no edges. Right now, this much smaller graph do not seems to be useful, but let's see what happens if we consider this situation for not only one, but for a block of new edges.
. What does it look like? Sure, Ti' is a forest with two trees (components). And if we condense these two components, we'll get a much smaller graph with precisely two vertices and no edges. Right now, this much smaller graph do not seems to be useful, but let's see what happens if we consider this situation for not only one, but for a block of new edges.
Now, imagine the MST Mi computed right after adding all the edges of the i-th block Bi. The graph 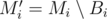 is a minimum spanning forest with at most
is a minimum spanning forest with at most 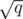 components, because the removal of an edge increases the number of components in exactly one and we are considering the removal of at most
components, because the removal of an edge increases the number of components in exactly one and we are considering the removal of at most 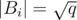 edges. Therefore, a condensation would produce a set Si of at most
edges. Therefore, a condensation would produce a set Si of at most 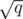 vertices. Let's write X to denote the total sum of the weights of the condensed edges (the internal edges of the components).
vertices. Let's write X to denote the total sum of the weights of the condensed edges (the internal edges of the components).
Compute a MST for the set Si considering only the edges added before the i-th block. This MST will have at most 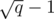 edges. If use the edges of this MST to initialize and maintain a multiset M of edges, we can insert a new edge in M and run Kruskal's algorithm
edges. If use the edges of this MST to initialize and maintain a multiset M of edges, we can insert a new edge in M and run Kruskal's algorithm 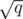 times, once per query. Over all blocks, we'll run Kruskal's algorithm q times for graphs with at most
times, once per query. Over all blocks, we'll run Kruskal's algorithm q times for graphs with at most 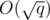 vertices and edges. For the j-th query, we should output X + Yj, where Yj is the total sum of the weights of the edges chosen by Kruskal's algorithm.
vertices and edges. For the j-th query, we should output X + Yj, where Yj is the total sum of the weights of the edges chosen by Kruskal's algorithm.
In a step-by-step description, the algorithm is as follows:
- Store the m initial edges in a multiset
edges. - Compute
large, an array with the edges of a MST for the initial m edges (Kruskal's for m edges). - For each block [l, r]:
-
- Create an empty array
initialand swap the contents withlarge.
- Create an empty array
-
- Insert edges
e[i]in the multisetedges, l ≤ i ≤ r.
- Insert edges
-
- Recompute
largefor the new state ofedges(Kruskal's for O(m + q) edges).
- Recompute
-
- Use
largeto find the forest, condense its components and to find the value of X.
- Use
-
- Create a multiset
Mof edges and useinitialand the condensed components to fill it with at most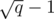 edges.
edges.
- Create a multiset
-
- For each edge
e[i], l ≤ i ≤ r:
- For each edge
-
-
- Insert
e[i]inM.
- Insert
-
-
-
- Compute Kruskal's minimum weight Y for the multiset
Mand output X + Y (Kruskal's for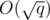 edges).
edges).
- Compute Kruskal's minimum weight Y for the multiset
-
We run Kruskal's algorithm 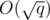 times for a graph with O(m + q) edges and q times for a graph with
times for a graph with O(m + q) edges and q times for a graph with 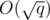 edges, so the total running time is around
edges, so the total running time is around 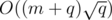 , if we have a fast DSU implementation.
, if we have a fast DSU implementation.
Here is my AC implementation:
Problems
I think that this problem can also be solved with some adaptation of this algorithm. If anyone knows any other problems suitable for this technique, just comment and I'll add them here!






